Влияние дислокаций на показатель преломления AlN с помощью наномасштабного поля деформации

Введение

Материалы на основе AlN являются многообещающими материалами для изготовления оптоэлектронных устройств глубокого ультрафиолета (DUV), таких как светодиоды (LED) [1,2,3,4,5], лазерные диоды [6,7,8] и фотодетекторы [ 9, 10] за счет прямой перестройки запрещенной зоны от 3,4 до 6,2 эВ [11]. Показатель преломления AlN напрямую влияет на характеристики оптоэлектронных устройств. Для светодиодов показатель преломления AlN влияет на эффективность извлечения света (LEE), поскольку полный угол внутреннего отражения определяется разницей показателя преломления между слоем AlN и другой областью, что является ключевым ограничивающим фактором для количества светоотдачи. Поскольку внешняя квантовая эффективность (EQE) является продуктом внутренней квантовой эффективности и LEE, показатель преломления AlN будет влиять на EQE светодиодов. Кроме того, показатель преломления играет ключевую роль при проектировании волноводных структур, таких как распределенный брэгговский отражатель (DBR) [12,13,14], коэффициент отражения которого зависит от показателя преломления. Поэтому выявление факторов, влияющих на показатель преломления AlN, важно. Из предыдущих исследований можно узнать, что на показатель преломления AlN могут влиять многие факторы, включая температуру, давление и ширину запрещенной зоны. Показатель преломления AlN увеличивается с повышением температуры [15] и более низкого давления [16]. Для материала на основе AlN показатель преломления становится ниже с увеличением ширины запрещенной зоны [17]. Кроме того, дислокации в полупроводниках имеют большое влияние на свойства полупроводников и производительность устройств. Дислокации снимают напряжение в материалах [18]. Они также будут влиять на темновой ток и чувствительность фотодетекторов [19], а также на IQE нескольких квантовых ям [11, 20] и так далее. Однако мало исследований сосредоточено на влиянии различной плотности пронизывающих дислокаций (TDD) на показатель преломления AlN, хотя в материалах AlN наблюдаются высокие TDD, которые обычно варьируются от 10 ⁸ до 10 ⁹ см ^{- 2} заказы из последних отчетов [21,22,23]. Исследование корреляции между TDD и показателем преломления AlN является ключом к оптимизации характеристик оптоэлектронных устройств. В данной работе исследована зависимость различных TDD от показателя преломления AlN. Используются разные длины волн фотонов, например 633 нм, 365 нм и 280 нм. Результаты показывают, что дислокации приводят к уменьшению показателя преломления AlN. Результаты будут полезны при разработке и моделировании оптоэлектронных устройств на основе AlN, таких как светодиоды DUV и структуры DBR.

Методы

Чтобы изучить взаимосвязь между дислокациями и показателем преломления AlN, шаблоны AlN были выращены методом металлорганического химического осаждения из газовой фазы (MOCVD) на подложках c-сапфира, а затем отожжены при разных температурах для получения образцов AlN с разной плотностью дислокаций.>

При выращивании темплатов AlN методом MOCVD в качестве газов-прекурсоров использовались триметилалюминий и аммиак. В качестве газа-носителя использовался водород. Давление во время выращивания поддерживали на уровне 40 мбар. Температура роста и время зарождения слоя составляет около 955 ° C в течение 150 с, а затем повышается до 1280 ° C для высокотемпературного (HT) роста AlN. После 15-минутного высокотемпературного роста AlN прослойка AlN была выращена при 1050 ° C в течение 160 с. Наконец, температура роста была повышена до 1280 ° C для выращивания толстого HT AlN в течение 50 мин. Общая толщина пленки AlN составляет около 1,1 мкм.

После роста слоя AlN с помощью MOCVD шаблоны AlN были отожжены ex situ при 1500 ° C, 1600 ° C, 1700 ° C и 1750 ° C в течение 1 ч соответственно. Слой AlN без отжига был помечен как образец 1, а образцы после отжига от 1500 ° C до 1750 ° C были помечены как образцы 2-5. Для измерения TDD в образцах AlN использовалась дифракция рентгеновских лучей (XRD), и спектроскопическое эллипсометрическое (SE) измерение было выполнено для измерения показателя преломления. Спектры рамановского сдвига были адаптированы для характеристики напряженного состояния шаблонов AlN.

Результаты и обсуждение

На рис. 1 a и b показаны кривые качания XRD в плоскости (0002) и (10-12) для пяти образцов AlN. Можно заметить, что полная ширина на полувысоте (FWHM) XRC плоскости (0002) немного уменьшается, а полная ширина XRC плоскости (10–12) значительно уменьшается от образца 1 к образцу 5. Плотность дислокаций с винтом и краем Компонент может быть рассчитан с использованием FWHM плоскости (0002) и (10–12) XRC в соответствии с формулами (1) и (2):[24, 25].

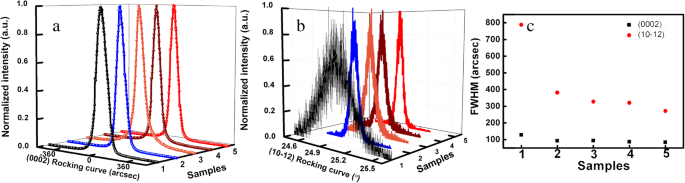
а XRC плоскости (0002) пяти образцов AlN. б XRC плоскости (10-12) пяти образцов AlN. c FWHM плоскости XRC (0002, 10-12); красный кружок означает FWHM плоскости (10-12), а черный квадрат представляет FWHM плоскости (0002)

где ρ _s и ρ _e представляют плотность дислокации с винтовой и краевой компонентами соответственно. β это FWHM XRC. | b _c | равняется c-осевой постоянной решетки, и | b _а | приравнивается к a-осевой постоянной решетки AlN. Полуширина XRC плоскости (0002) и (10–12) показана на рис. 1c для пяти образцов AlN, а рассчитанные TDD для пяти образцов AlN показаны в таблице 1.

Экспериментальные данные SE для пяти образцов подобраны программой CompleteEASE (J.A. Woollam Inc.) с использованием параметрической модели полупроводника, которая может эффективно воспроизводить оптические свойства полупроводников с прямой запрещенной зоной [26]. На рис. 2а показаны частичные экспериментальные и аппроксимирующие кривые для пяти образцов. Среднеквадратичная ошибка (MSE) для пяти выборок составляет 8,139, 8,536, 9,175, 10,560 и 9,821, соответственно, что подтверждает хорошие результаты подгонки. Все данные и результаты подгонки представлены в дополнительном файле 1.

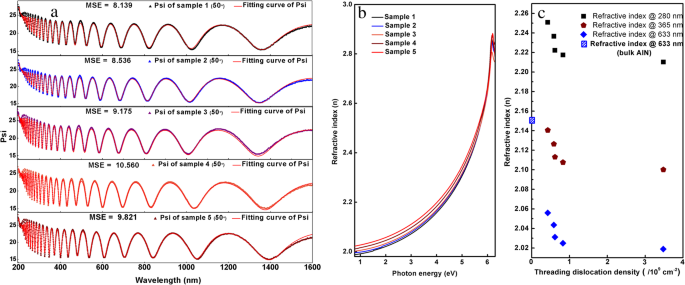
а Частичные экспериментальные данные измерений SE и аппроксимации кривых. б Кривая показателя преломления. c Показатель преломления в зависимости от различных TDD при 280 нм, 365 нм и 633 нм

Кривые показателя преломления пяти образцов могут быть получены из результатов подгонки, как показано на рис. 2b. Когда энергия фотонов ниже ширины запрещенной зоны AlN (около 6,2 эВ), показатель преломления увеличивается с увеличением энергии фотонов для всех пяти образцов. Однако, когда энергия фотона превышает 6,2 эВ, показатель преломления уменьшается с увеличением энергии фотона. Это явление можно описать дисперсионным соотношением Крамерса – Кренига. С уменьшением TDD в AlN показатель преломления увеличивается с 2,019 до 2,056 при 633 нм, что ближе к показателю объемного AlN (2,15 при 633 нм [27]). Это означает, что дислокации в AlN делают показатель преломления меньше, чем у массивного кристалла AlN.

Зависимость между показателем преломления и TDD при 4,42 эВ (280 нм, солнечный слепой УФ), 3,40 эВ (365 нм, запрещенная зона GaN) и 1,96 эВ (633 нм) показаны на рис. 2c, а также в таблице 1. Видно, что показатель преломления AlN уменьшается с увеличением TDD. При увеличении плотности дислокаций с 4,24 × 10 ⁸ до 3,48 × 10 ⁹ см ^{- 2} показатель преломления AlN уменьшается с 2,2508 до 2,2102 при 280 нм.

Чтобы выявить механизм изменения показателя преломления AlN дислокациями, изучается поле деформации, создаваемое дислокациями. Связь между показателем преломления и полем деформации описывается формулой (3) [28]:

В формуле p _ij - упругооптический тензор и S наличие напряжения. Матрица фотоупругих констант P вюрцита AlN показано выражением (4) [29, 30].

Рассмотрены матрицы полей деформации винтовой и краевой дислокаций в AlN. Цилиндрические кольцевые модели двух типов дислокации описаны на рис. 3. Согласно моделям, можно получить распределение поля деформации вокруг одиночной дислокации [31, 32].

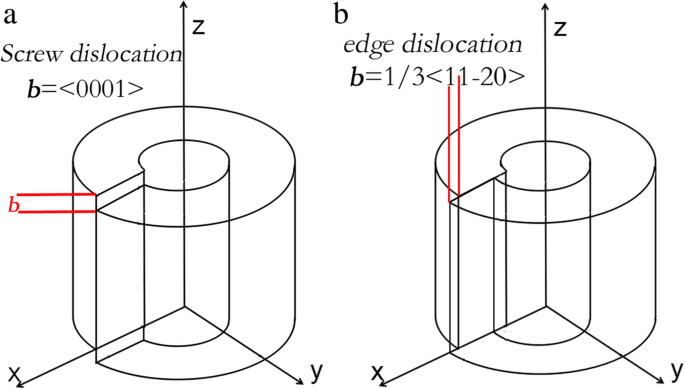
Цилиндрическая кольцевая модель а винтовой вывих и б краевой вывих

Поле деформации вокруг единичной винтовой дислокации можно записать как:

Поле деформации вокруг единичной краевой дислокации можно записать как:

где b - длина вектора Бюргерса единичной дислокации, а e представляет собой деформацию вокруг дислокации. G =121 ГПа - модуль сдвига вюрцита AlN; λ =117,1 ГПа и v =0,241 - постоянная хромоты и коэффициент Пуассона [33, 34] соответственно. Согласно переписке между e _ij и S _k ( я , j = x , y , z ; к =1,2,3 ... 6) [35], мы преобразуем поле деформации в формирование матрицы, как показано ниже, чтобы дополнительно представить изменение показателя преломления, вызванное дислокациями.

Взяв матрицы (7) и (8) в формулу (3), мы можем получить выражение Δ n вызвано смещением единичного винта и края агрегата.

На основе расчетов распределения показателя преломления (возьмем, например, показатель преломления при 633 нм) вокруг единичного винта и единичных краевых дислокаций, показаны на рис. 4. Он показывает, что показатель преломления вокруг дислокации изменяется в радиальном направлении. от ядра дислокации, которое можно рассматривать как неоднородную среду. Таким образом, распространение света в AlN будет соответственно зависеть от TDD. Рассеяние и интерференция будут происходить [36], когда свет проходит через эти преломляющие поля вокруг дислокаций. В результате изменится показатель преломления AlN, что соответствует матрице рассеяния неоднородной среды [37].

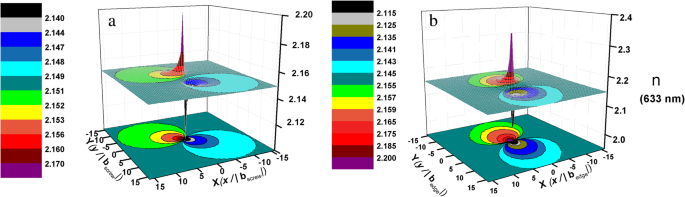
Распределение показателя преломления при 633 нм вокруг a узел винтовой дислокации и b единичная краевая дислокация

Как упоминалось в разделе «Введение», следует избегать других факторов влияния, чтобы доказать, что на показатель преломления действительно влияют дислокации. Все образцы были измерены при комнатной температуре, чтобы избежать влияния температуры. Чтобы избежать влияния напряжения в материале AlN, был взят рамановский спектр для подтверждения напряжения в AlN, и результаты показаны на рис. 5. E _г пик моды сапфира на 750 см ^{- 1} принимается за калибровку. Пик рамановского сдвига AlN E ₂ ( h ) синий сдвигается с уменьшением TDD, как показано в таблице 1. Синий сдвиг E ₂ ( h ) пик означает, что AlN испытывает все большее и большее сжимающее напряжение от сапфировой подложки. Однако с увеличением сжимающего напряжения показатель преломления становится ближе к показателю преломления массивного AlN на длине волны 633 нм. Можно четко получить, что напряжение AlN, испытываемое неоднородными подложками, мало влияет на показатель преломления. Дополнительным доказательством, подтверждающим вывод, является то, что показатель преломления AlN также меньше, чем у объемного AlN, когда AlN испытывает растягивающее напряжение от подложки Si [38], что совпадает с условием, что AlN испытывает сжимающее напряжение в этой работе. Это явление можно объяснить тем фактом, что напряжение AlN, которому подвержены подложки, слишком мало, чтобы существенно изменить показатель преломления AlN. В результате, по сравнению с влиянием других факторов, влиянием напряжения от подложек на показатель преломления AlN можно пренебречь.

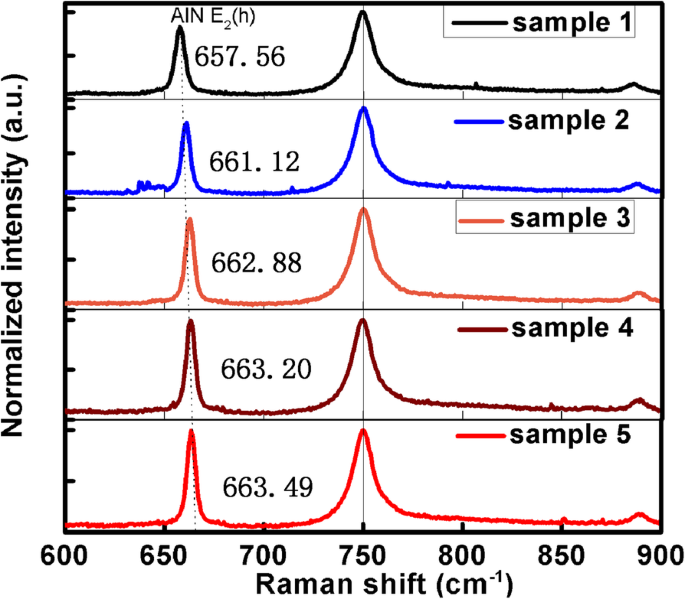
Спектры комбинационного сдвига пяти образцов

Здесь также рассчитывается ширина запрещенной зоны для пяти образцов. Коэффициент оптического поглощения α извлекается из результатов подгонки SE, а затем ширина запрещенной зоны E _г рассчитывается по формуле ниже [39]:

Сюжет ( αE ) ² по сравнению с E представлен на рис. 6. Пересечение x -axis - значение E _г . От точки пересечения аппроксимирующих кривых на x По оси, увеличивающаяся ширина запрещенной зоны с 6,1106 до 6,1536 эВ для образца 1 - образца 5 показана на рис. 6. Соотношение между показателем преломления и шириной запрещенной зоны показано ниже [16].

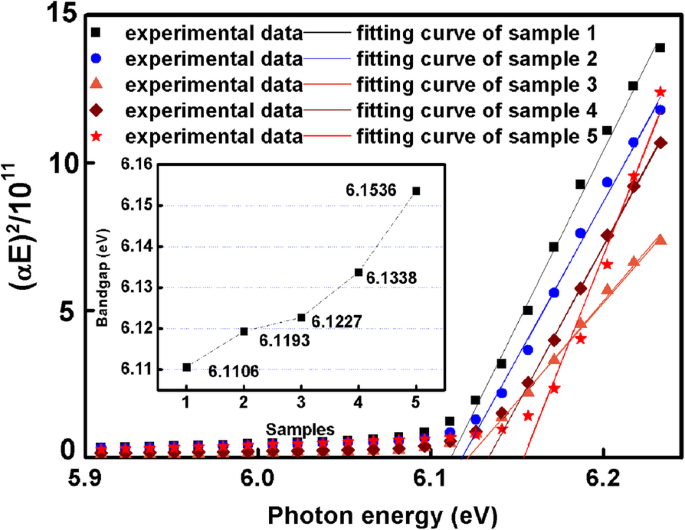
Зависимость ( αE ) ² на ( E ), на вставке показана запрещенная зона шаблонов AlN

где E - энергия фотона, а E _г - ширина запрещенной зоны AlN. а и b - константы, равные 13,70 и 7,81 для AlN соответственно. Показатель преломления AlN должен уменьшаться с увеличением E _г по формуле. Однако в этой работе показатель преломления AlN увеличивается с увеличением E _г , что означает, что влиянием ширины запрещенной зоны на показатель преломления AlN можно пренебречь по сравнению с влиянием TDD. Следовательно, изменение TDD играет ключевую роль в изменении показателя преломления AlN.

В сочетании с приведенным выше анализом подтверждается, что поле деформации в наномасштабе будет влиять на распределение показателя преломления вокруг дислокаций, что дополнительно влияет на показатель преломления AlN. Согласно экспериментальным данным, дислокации уменьшат преломление AlN.

Выводы

В заключение, влияние TDD на показатель преломления AlN исследовано экспериментально и теоретически. Исключая влияние температуры, напряжения и ширины запрещенной зоны, можно сделать вывод, что показатель преломления AlN уменьшается с увеличением TDD. Дальнейшие исследования показали, что наноразмерное поле деформации вокруг дислокаций приводит к значительному изменению показателя преломления вокруг дислокаций. Рассеяние и интерференция будут происходить, когда свет распространяется через дислокации, и, таким образом, показатель преломления AlN будет изменен. Результаты этой работы будут полезны для оптимизации оптоэлектронных устройств DUV на основе AlN.

Доступность данных и материалов

Все данные могут быть предоставлены по соответствующему запросу.

Сокращения

DBR:

Распределенный брэгговский отражатель

DUV:

Глубокий ультрафиолет

EQE:

Внешняя квантовая эффективность

FWHM:

Полная ширина на половине максимальной

светодиоды:

Светодиоды

LEE:

Эффективность вытяжки света

MOCVD:

Металлоорганическое химическое осаждение из паровой фазы

MSE:

Среднеквадратичная ошибка

SE:

Спектроскопическая эллипсометрия

TDD:

Плотность заправки дислокаций

XRC:

Кривая качания XRD

XRD:

Рентгеновская дифракция