Магические математические формулы для нанобоксов

Аннотация

Полые наноструктуры находятся в авангарде многих научных исследований. Они состоят из нанобоксов, наноклеток, нанокадров и нанотрубок. Мы исследуем математику координации атомов в нанобоксах. Такие конструкции состоят из полого ящика с n снаряды и t внешние слои. Полученные нами магические формулы зависят как от n и t . Мы находим, что нанобоксы с t =2 или 3, или стенки с несколькими слоями обычно имеют объемно-скоординированные атомы. Показано, что преимущества низкой координации в наноструктурах проявляются только тогда, когда толщина стенки намного меньше, чем обычно синтезируется. Случай, когда t =1 уникален и имеет различные магические формулы. Такие низкокоординированные нанобоксы представляют интерес для множества приложений, включая батареи, топливные элементы, плазмонные, каталитические и биомедицинские применения. По этим формулам можно определить поверхностную дисперсию нанобоксов. Мы ожидаем, что эти формулы будут полезны для понимания того, как атомная координация изменяется в зависимости от n и t внутри нанобокса.

Введение

Первоначально нанобоксы были синтезированы примерно в 2002 г. [1, 2]. Нанобокс отличается от наноклетки тем, что последняя имеет пористые стенки. Кроме того, оба они отличаются от нанофрейма тем, что нанофрейм представляет собой структуру (фрейм), состоящую из низкокоординированного контура кластера. Такие анизотропные многогранные структуры могут быть созданы в результате реакций гальванического смещения [3, 4]

$$ \ begin {array} {l} \\ {\ hbox {Anode}}:yA _ {(s)} \ rightarrow yA _ {({{\ rm aq}})} ^ {x +} + xye _ {({{ \ rm aq}})} ^ {-} \\ {\ hbox {Cathode}}:xB _ {({{\ rm aq}})} ^ {y +} + xye _ {({{\ rm aq}})} ^ {-} \ rightarrow xB _ {(s)} \\ {\ hbox {Full \, Reaction}}:yA _ {(s)} + xB _ {({{\ rm aq}})} ^ {y +} \ rightarrow yA _ {({{\ rm aq}})} ^ {x +} + xB _ {(s)} \\ \ end {array} $$ (1)

где нанокластер с металлом A жертвенно выдолблен водным раствором металла B , который имеет более высокий восстановительный потенциал и создает полое твердое тело элемента B . Половинные реакции происходят на аноде и катоде электрохимической ячейки, что приводит к полной комбинированной реакции, как указано выше [5]. В некоторых случаях ученые объединили гальваническое смещение с образованием пустот посредством диффузии металлов и вакансий по Киркендаллу-Фику [6]. Модели этой активности существуют для конкретных случаев, и сообщалось об экспериментах по электронной микроскопии in situ [7, 8]. Другие методы синтеза включают химическое травление [9], ионный обмен [10] и металлорганические каркасы (MOF) [11, 12]. В недавнем обзоре методов синтеза упоминается, что анизотропные кластеры еще не созданы в области размеров \ (2

Такие полые структуры имеют низкую координацию, что делает их интересными для батарей [12], топливных элементов [14], плазмонных [15], каталитических [16] и биомедицинских приложений [17]. Предыдущий анализ показывает, что для каталитических приложений применяется координационный подход [18], в то время как для накопления энергии есть только некоторые подсказки с результатами теории функционала плотности (DFT), указывающие на важность выбранных аспектов [19]. Мы используем метод, ранее полученный из анализа матрицы смежности [20, 21], чтобы обнаружить атомарную координацию бокса с n оболочки и толщина стенки t слои. Этот анализ показывает, что нанобокс с t =2 или 3 имеет объемную координацию, и поэтому преимущества низкой координации присутствуют только для нанобоксов с более тонкими стенками, чем обычно считается необходимым. Используемые нами методы количественно определяют атомную координацию с помощью магических чисел и формул для тринадцати типов нанобоксов.

Методы

Ключом к нашему анализу методами координации является создание матрицы смежности из атомных координат нанобокса. Такая матрица создается следующим образом. Мы определяем i и j в качестве ближайших соседей и отделите их от остальных, потребовав, чтобы длина связи \ (r_ {ij} $$ {\ mathbf {A}} (i, j) =\ left \ {\ begin {array} {ll} 1 &{\ quad} \ hbox {if} r_ {ij} описывает матрицу смежности для кластера, и

$$ {\ mathbf {E}} (i, j) =\ left \ {\ begin {array} {ll} r_ {ij} &{\ quad} \ hbox {if} \, r_ {ij} описывает евклидову матрицу для ящика. Мы используем евклидову матрицу для определения диаметра, D , (нм) для нанобоксов.

Поскольку мы создаем матрицы смежности ближайших соседей, мы знаем координационное число \ (\ hbox {cn} _i \) вершины i суммируя элементы \ ({{\ mathbf {A}}} (i,:) \). Наша структура состоит из \ (n + 1 \) оболочек с номерами 0, 1, ..., n , с t внешние слои. Пусть \ (N _ {{\ rm cn} _i} (n, t) \) будет числом атомов с координацией \ (\ hbox {cn} _i \), где \ (1 \ le \ hbox {cn} _i \ le \ hbox {cn} _M \) с \ (\ hbox {cn} _M \) максимальной согласованностью в нанобоксе. Тогда общее количество атомов в нанобоксе равно

$$ N_T (n, t) =\ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _M} {N _ {{\ rm cn} _i} (n, t)}. $$ (4)

Поверхностные атомы во внешней оболочке (или внутри) нанобокса, n иметь набор связок меньше объемного согласования. Таким образом, максимальная координация для поверхностных атомов равна \ (\ hbox {cn} _s <\ hbox {cn} _M \), а количество поверхностных атомов

$$ N_S (n, t) =\ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _s} {N _ {{\ rm cn} _i} (n, t)}. $$ (5)

Это верно, если все неповерхностные вершины имеют координацию больше, чем \ (\ hbox {cn} _s \), что верно для всех кластеров fcc, bcc и hcp. Мы определяем \ (N _ {{\ rm cn} _i} (n, t) \) путем подсчета столбцов матрицы смежности, сумма которых равна \ (\ hbox {cn} _i \). Обратите внимание, что наш алгоритм координат кластера построен с помощью командных интерпретаторов, поэтому каждая последующая оболочка содержит все предыдущие более низкие значения n . Кроме того, количество облигаций в коробке

$$ N _ {{\ rm B}} (n, t) =\ frac {1} {2} \ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _M} {\ hbox { cn} _i \ cdot N _ {{\ rm cn} _i} (n, t)}, $$ (6)

где \ (N _ {{\ rm B}} (n, t) \) - количество связей, а \ (\ hbox {cn} _M \) - максимальная координация. Коэффициент 1/2 возникает из-за попарного связывания ближайших соседей.

Поскольку мы знаем, что эти уравнения зависят от n , t как полином степени не выше 3, мы можем вычислить \ (N _ {{\ rm cn} _i} (n, t) \) для 4 последовательных значений n , скажем, \ (n =n_0 + j \), j =0, 1, 2, 3. Тогда простой интерполирующий полином даст коэффициенты полинома. Необходимо проверить, что при увеличении \ (n_0 \), которое обычно равно 1, формулы не меняются. Если формулы становятся устойчивыми с \ (n_0 \) и далее, то они верны для всех \ (n \ ge n_0 \). Чтобы получить точные рациональные коэффициенты, необходимо решить систему Вандермонда для коэффициентов в точной арифметике.

Обратите внимание, что в магических формулах для нанобоксов мы имеем \ (n> t \), поэтому, вопреки всем ожиданиям, заполнение коробки соответствующим выбором t не будет воссоздавать исходные магические формулы для полных твердых кластеров. Эти волшебные формулы полезны для моделирования мезомасштабных свойств кластеров и ящиков или клеток. Полные наборы формул изначально были получены для девятнадцати типов кластеров. В этой рукописи мы выводим магические формулы для тринадцати типов нанобоксов.

В приведенных ниже магических формулах мы обнаруживаем, что объемная координация может проявляться либо для t =2 или t =3 слоя толщины оболочки. Большинство из них предназначены для слоев, где t =2; Исключениями являются куб с ГЦК, кубооктаэдр, икосаэдр, куб и усеченный куб. В последнем случае объемная координация появляется только для t =3 слоя. Для данных, представленных ниже, таблицы магических формул сопровождаются фигурой «полукорпуса», чтобы показать внутреннюю часть нанобоксов. Рядом находится цветная полоса, указывающая согласование и количество таковых в скобках.

Результаты и обсуждение

Чтобы обозначить применимость магических формул, мы обрисовываем, как каталитическое поведение может зависеть от координации и подобных формул. Мы определяем G как зависящая от размера энергия Гиббса кластера. Из-за того, что адатомы связаны с атомами внешней оболочки, увеличивается G это называется энергией адсорбции и обозначается как \ (\ Delta G \). Это может быть разделено на различные типы координации атомов на внешней оболочке, связанных с адатомами. Например, атом кинка добавляет к энергии адсорбции величину \ (\ Delta G_ {k} \). Точно так же реберный атом добавляет \ (\ Delta G_ {e} \), а фасетный атом вносит \ (\ Delta G_f \), затем [18]:

$$ \ Delta G =\ sum _ {o \ in \ {f, e, k \}} \ Delta G_o N_o $$ (7)

где \ (N_o \) - количество атомов во внешней оболочке указанного типа. Общее количество атомов во внешней оболочке, связанных с адатомами, определяется как \ (N_s =N_f + N_e + N_k \), в результате чего:

$$ \ begin {align} \ Delta G =&{} \ Delta G_f \ cdot (1-f_e-f_k) + \ Delta G_e \ cdot f_e + \ Delta G_k \ cdot f_k \\ &\ quad {\ hbox {where} } \, \, f_o =N_o / N_s, \, \, o \ in \ {e, k \}, \ end {align} $$ (8)

с долей энергии Гиббса, выраженной через ребра и узлы перегиба, которые имеют явную координацию для конкретных структур. Это демонстрирует, что магические формулы играют роль в поверхностных реакциях через координацию ребер и изломов и их формулы. Обратите внимание, что уравнение. (8) применяется к адсорбции на верхних участках, в противном случае не все адатомы будут связаны с атомами во внешней оболочке. В такой модели участки перегиба имеют магические формулы, которые зависят от количества оболочек, n , крайние сайты имеют формулы, линейные с n , а фасетные сайты имеют формулы, квадратичные с n . В частности, сайты излома представляют собой формулы с самой низкой скоординированностью, краевые сайты являются вторыми по уровню скоординированности, а сайты фасетов имеют cn =8 для (100) фасетов и cn =9 для фасетов (111).

Могут применяться два фундаментальных соотношения для отдельных частиц. Для энергии Гиббса и константы адсорбции \ (K _ {{\ rm a}} \) справедливо:

$$ K _ {{\ rm a}} ={\ exp} \ left (- \ frac {\ Delta G} {RT} \ right), $$ (9)

где R - газовая постоянная, а T это температура в Кельвинах. Кроме того, соотношения Бренстеда – Эванса – Поланьи широко используются в гомогенном и гетерогенном катализе [18, 22] с использованием соотношения для констант реакций k и константы равновесия K следующим образом:

$$ k =gK ^ {\ alpha}, \ quad 0 <\ alpha <1, $$ (10)

где g и \ (\ alpha \) (параметр Поляни) являются константами. Параметр Поланьи не имеет единиц измерения и является правильной дробью, как это первоначально было дано Бренстедом [23]. Тогда у нас есть:

$$ k =k '_ {a} {\ exp} \ Bigl (- \ alpha \ bigl ({f_n ^ {e} \ cdot \ chi _ {_ e} ({D_n}) + f_n ^ {k} \ cdot \ chi _ {_ k} ({D_n})} \ bigr) \ Bigr), $$ (11)

где

$$ \ begin {align} &\ chi _ {_ e} (D) =\ frac {\ Delta G_e (D) - \ Delta G_f (D)} {RT}, \\ &\ chi _ {_ k} (D ) =\ frac {\ Delta G_k (D) - \ Delta G_f (D)} {RT}, \ end {align} $$ (12)

$$ k '_ {a} =g \ exp \ left (- \ alpha \ frac {\ Delta G_f} {RT} \ right). $$ (13)

Этот анализ показывает, что для определения каталитической модели необходим метод расчета энергии Гиббса. Были рассмотрены известные каталитические реакции, такие как двухступенчатый механизм и механизм Ленгмюра – Хиншелвуда [24].

Нанобоксы FCC

Гранецентрированные кубические структуры являются наиболее распространенной формой нанокластеров и нанобоксов. Это структура металлов с интересными свойствами, таких как благородные металлы с плазмонными свойствами и каталитические драгоценные металлы. Поскольку золото имеет высокий потенциал восстановления 1,50 В (см. Уравнение 1) по сравнению со стандартным водородным электродом (SHE) [5], это один из самых простых металлов для синтеза в виде нанобокса или наноклетки. Золотые нанобоксы или наноклетки были сформированы в форме куба [1], кубооктаэдра [25], икосаэдра и декаэдра [26], октаэдра [27] и тетраэдра [28].

Мы можем определить приблизительный размер этих нанобоксов, используя подход координации для длины связи ближайшего соседа r (сп) [29],

$$ r (cn) =\ frac {2r _ {{\ rm B}}} {\ left (1+ \ exp \ left (\ frac {12 - \ langle cn \ rangle _c)} {8 \ cdot \ langle cn \ rangle _c} \ right) \ right)}. $$ (14)

Здесь \ (r _ {{\ rm B}} \) - объемная длина связи для золота (0,2884 нм), а \ (\ langle cn \ rangle _c \) - средняя координация кластера. Мы находим линейную зависимость между D и н , количество оболочек кластера, как показано в Таблице 1:

$$ D (n) =a \ cdot r _ {{\ rm B}} \ cdot n + b. $$ (15)

Мы используем нанобоксы с t =3, так как формулы меняются в зависимости от t , и мы хотим достичь некоторой общей координации. Для расчета D ( нет ), мы используем максимальное расстояние между атомами в кластере, полученное из евклидовой матрицы. Обратите внимание, что D ( нет ) представляет собой эмпирическую формулу, полученную на основе данных (варьируются n и вычислим D ), и как таковое не доказано.

Эти зависимости дают диаметры в соответствии с другими данными из DFT. Для твердых кубооктаэдров с N равные 55, 561 и 923, получаем диаметры 1,12 нм, 2,85 нм и 3,43 нм. Это выгодно отличается от опубликованных результатов DFT для 55 атомов размером 1,1 нм [30], для 561 атома 2,7 нм [31] и для 923 атомов 3,5 нм [30]. Магические формулы для некоторых нанобоксов ГЦК приведены в таблице ниже (Таблицы 2, 3, 4, 5, 6, 7, 8).

Икосаэдрические и декаэдрические нанобоксы

См. Таблицы 9 и 10.

Алмазные и простые кубические нанобоксы

Структура кубической решетки алмаза образована аллотропом углерода, а также элементами кремния и германия. Также эту структуру образуют некоторые кубические соединения, такие как кубический оксид железа, тетраэдрический алмазный маггемит \ (\ gamma \) - Fe ₂ О ₃ . Длина связи Fe – O в тетраэдрическом алмазном маггемите \ (\ gamma \) - Fe ₂ О ₃ =0,186 нм [32]. Это приводит к диаметру кластеров алмаза D ( нет ), как показано ниже:

$$ D (n) =3,3984 \ cdot n _ {{\ rm B}} \ cdot n - 0,21194. $$ (16)

Согласно ссылке [12], микробоксы из кубического оксида железа образовывались и обладали интересными способностями хранения лития. Мы не знаем полной модели координации для хранения энергии, но, как упоминалось выше, результаты DFT показывают, что активность может зависеть от ориентации фасеток [19]. В настоящее время не существует такой модели зависимости накопления от координации, как у нас для катализа. Из уравнения (16) выше (созданного с использованием t =4) для микробокса требуется примерно n =1600 снарядов для алмазного маггемита. Магические формулы для структур алмаза и простой кубической решетки перечислены ниже (Таблицы 11, 12).

Нанобоксы скрытой копии

См. Таблицы 13, 14 и 15.

Нанобоксы HCP

См. Таблицу 16.

Дело t =1

Частный случай t =1 уникален и, как таковой, имеет различные магические формулы. Мы исследуем этот случай для некоторых из вышеперечисленных нанобоксов. Нанобоксы с ультратонкими стенками были сформированы кубической [33], октаэдрической [16] и икосаэдрической формы [34]. Согласно приведенным ниже магическим формулам кубический нанобокс с t =1 имеет самую низкую координацию. Платина имеет относительно высокий потенциал восстановления 1,18 В по сравнению с SHE, поэтому она может быть образована гальванической заменой, см. Уравнение. (1) [5]. Однако свойства реакции окисления и восстановления (ORR) некоторых из этих наноклеток на основе платины показывают, что структуры с гранями (111), в отличие от граней (100), имеют лучшую массовую активность ORR [35].

Таким образом, икосаэдр с 20 (111) гранями имеет лучшую массовую активность ORR, за ним следует октаэдр и, наконец, усеченный куб. Об этом свойстве каталитического поведения из-за того, что ориентация граней превалирует над координационным числом, свидетельствуют табличные данные, представленные ниже. Другими словами, как указано в следующих таблицах, куб с гранями (100) имеет самые низкие магические координационные числа с четырьмя и пятью, но октаэдр и икосаэдр с гранями (111) и более крупными магическими формулами имеют лучшую активность ORR. Это свойство проявляется также в нанокластерах, где результаты DFT подтверждают преобладание граней (111) [36], особенно для сплавов PtNi (таблицы 17, 18, 19, 20, 21).

Дисперсия

Учитывая важность краевых и узловых участков по сравнению с фасетными с точки зрения каталитической активности, мы определили поверхностную дисперсию для некоторых изучаемых нами нанобоксов. Грани (100) имеют cn =8, а фасеты (111) имеют cn =9. Это может дать представление о причинах индивидуальной полиэдрической активности при сравнении нанобоксов. На рис. 1 ниже мы строим график поверхностной дисперсии \ (D _ {{\ rm s}} =(N _ {{\ rm e}} + N _ {{\ rm k}}) / N _ {{\ rm S}} \ cdot 100 \% \). В этом соотношении \ (N _ {{\ rm k}} \) - это количество узловых или угловых узлов, а \ (N _ {{\ rm e}}} \) - количество граничных узлов. Как видно на рисунке 1, нанобоксы с поверхностями (111) в отличие от поверхностей (100) имеют более высокую дисперсию, что свидетельствует о предпочтении каталитической активности грани (111).

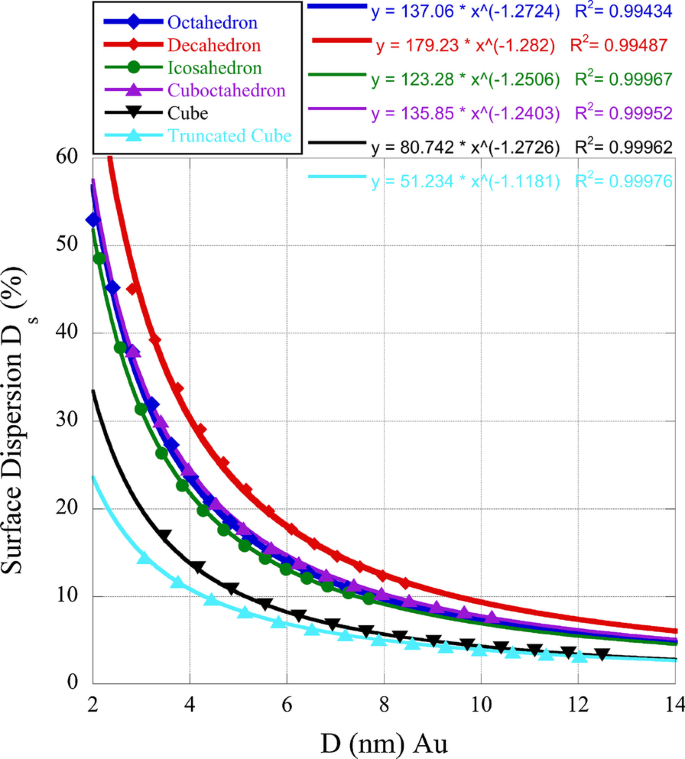
Поверхностная дисперсия золотых нанобоксов

Заключение

Таким образом, мы представили первое подробное математическое описание магических формул для нанобоксов. Случай толщины оболочки, t =1 отличается от \ (t> 1 \), и мы заносим в таблицу данные для некоторых из этих случаев. Перечислены формулы для координации, числа атомов и числа связей. Мы обнаружили, что объемная координация появляется для слоев, где t =2 или 3, и поэтому он намного тоньше, чем обычно синтезируемый. Преимущества низкой координации достигаются только при очень тонких стенах. Мы ожидаем, что эти результаты будут полезны для моделирования и экспериментальной работы.

Доступность данных и материалов

Наборы данных, подтверждающие выводы этой статьи, можно получить у соответствующего автора.

Сокращения

скрытая копия:: Тело центрированное кубическое
fcc:: Кубическая грань центрированная
hcp:: Гексагональный плотно упакованный
DFT:: Функциональная теория плотности
ОНА:: Вторичный водородный электрод

Количественная оценка клеточной интернализации полимерных наночастиц в раковых клетках гортани и иммунных … Двойной четырехквадрантный фотодетектор на основе черного кремния с нанометровым усилением в ближнем инфра…

Наноматериалы