Магические математические отношения для нанокластеров

Введение

Магические числа и формулы для нанокластеров имеют долгую историю, восходящую к пророческой публикации ван Хардевельда и Хартога в 1969 году [1]. Их идеи появились еще до эры нанонауки. С тех пор мы стали свидетелями появления магических чисел в двумерных многоугольниках и трехмерных многогранниках [2], углеродных фуллеренах [3] и, в ограниченном объеме, снова в кластерах [4]. Такие разнообразные материалы, как кремний [5], бор [6], а фактически более 1000 публикаций из службы индексирования Web of Science относятся к магическим числам в кластерах. Изучение размера и формы нанокластеров важно для современного общества, поскольку это определяет не только внутренние физические и химические свойства, но также актуальность для оптических, каталитических, электронных и магнитных приложений [7]. Наша цель - обновить базу данных этих знаний с учетом текущих отношений и данных, теперь, когда мы вошли в нано-область.

Возникновение магических чисел в нанокластерах связано, прежде всего, с образованием атомных оболочек на фундаментальной ячейке. Когда количество атомов составляет полную оболочку, мы находим уникальный набор чисел, называемый «магическим», который определяет оболочки атомов. Кластер представлен графом, в котором атомы являются вершинами, а связи - ребрами. Он состоит из вложенных друг в друга ракушек, похожих на слои луковицы. Мы определяем количество слоев как n и обнаружить математические соотношения между координационными числами ближайшего соседа, связями, общим числом атомов и некоторыми топологическими индексами в зависимости от n . В оригинальной статье ван Хардевельда и Хартога [1] рассматривались ГЦК, ОЦК и ГПУ кластеры. Ссылка Тео и Слоана [2] рассматривает многогранники и Платоновы тела, но не учитывает взаимосвязь координационных чисел ближайшего соседа. Мы добавляем в эту базу данных, рассматривая простые кубические, алмазно-кубические и платоновые тела, в дополнение к топологическим свойствам и дисперсии кластеров.

Переход размера от объемного к кластерам из нескольких атомов на самом деле связан с соотношением поверхностных атомов по сравнению с объемными атомами. Такие свойства, как каталитическая химия, поверхностный плазмонный резонанс и фотолюминесценция оптических квантовых точек [8], зависят от координации и количества поверхностных атомов. Дисперсия или относительный процент поверхностных атомов определяется отношением поверхностных атомов к общему количеству атомов, как было рассмотрено ранее [9]. Наш анализ определит относительное ранжирование дисперсии с точки зрения геометрии кластера.

Топологические индексы начались с оригинальной статьи Винера о его индексе и температурах кипения парафина [10]. Лишь некоторое время спустя Хосоя ввел математический аппарат для анализа топологических индексов [11]. Ранее мы ввели топологические индексы и нанокластеры [12]. На момент написания этой статьи существует множество индексов, некоторые из которых зависят от матрицы смежности или расстояния. Мы показываем здесь, что во многих формах кластера существуют магические математические отношения для четырех индексов как функции от n и количество снарядов.

Методы

Для каждого из исследуемых нами типов кластеров мы создаем вычислительный алгоритм, который определяет атомные координаты кластеров. Затем мы приступаем к созданию матрицы смежности и матрицы расстояний, определяемой следующим образом. Матрица смежности A создается там, где мы определяем i и j как ближайших соседей и отделите их от остальных, потребовав, чтобы r _ij < г _c , где r _c - пороговое значение, немного выше расстояния до ближайшего соседа, но меньше расстояния до второго соседа. Таким образом,

где r _ij это евклидово расстояние между атомом i и атом j . Подходящее значение для r _c равно 1,32 · r _мин , где r _мин наименьшая длина связи. Это относится как к додекаэдрической структуре, так и к другим, которые мы изучаем. Координационные числа кластера - это просто количество ненулевых элементов в столбце матрицы смежности. Матрица расстояний определяется как

$$ \ mathbf {D} (i, j) =\ left \ {\ begin {array} {ll} 0 &i =j \\ d_ {ij} &i \ neq j \ end {array} \ right. $$ (2)

где d _ij - длина кратчайшего пути в графе из i к j . Существует эффективный алгоритм вычисления матрицы расстояний из матрицы смежности [13]. Используя эти определения, мы можем вычислить индекс Винера, W ( G ), гипер-индекс Винера, W Вт ( G ), обратный индекс Винера rW ( G ), и индекс Сегеда, Sz ( G ), как подробно описано ранее [14]. В этих расчетах используется тот же алгоритм, который мы ранее использовали для топологических индексов и нанокластеров [12].

Предыдущие авторы предлагали доказательства магических отношений, которые мы сокращаем в наших обозначениях, относящихся к работе, представленной здесь [1, 2]. Поскольку мы создаем матрицы смежности ближайших соседей, мы знаем координационное число c нет _я вершины i суммируя элементы A ( я , :). Наша структура состоит из n +1 снаряды с номерами 0,1,…, n . Пусть \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) будет числом атомов с координацией c нет _я где 1≤ c нет _я ≤ c нет _M с c нет _M максимальная координация в кластере. Тогда общее количество атомов в кластере определяется как

$$ N_ {T} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {N _ {{cn} _ {i}} (n)}. $$ (3)

Поверхностные атомы внешней оболочки n иметь набор связок меньше объемного согласования. Таким образом, максимальная координация для поверхностных атомов составляет c нет _s < c нет _M , а количество поверхностных атомов

$$ N_ {S} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {s}} {N _ {{cn} _ {i}} (n)}. $$ (4)

Это верно, если все неповерхностные вершины имеют координацию больше, чем c нет _s , что верно для всех кластеров, но обратите внимание на расхождение для додекаэдров ниже. Мы определяем \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) путем подсчета столбцов матрицы смежности, сумма которых равна c нет _я . Обратите внимание, что наш алгоритм координат кластера построен с помощью командных интерпретаторов, поэтому каждая последующая оболочка содержит все предыдущие более низкие значения n . На рис. 1 показаны оболочки кластеров для ГЦК-куба и додекаэдра. Кроме того, количество облигаций в кластере

$$ N_ {B} (n) =\ frac {1} {2} \ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {{cn} _ {i} \ cdot N _ {{cn} _ {i}} (n)}, $$ (5)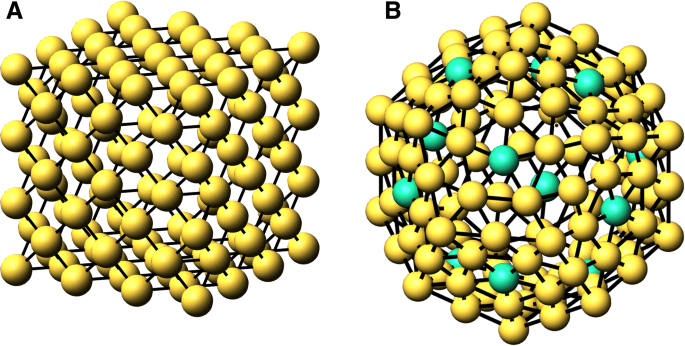

Оболочки атомов для n =3 для куба A. fcc и n =2 Б. додекаэдр. В B зеленые атомы (12) относятся к c нет =5 внутри оболочки

где N _B ( нет ) - количество облигаций, а c нет _M это максимальная согласованность. Коэффициент 1/2 возникает из-за попарного связывания ближайших соседей. Эта магическая взаимосвязь, по-видимому, не рассматривалась в предыдущих публикациях, за исключением нескольких кластеров, рассмотренных в [4]. Мы также отмечаем, что Тео и Слоан вывели общее количество атомов, поверхностных и внутренних атомов для кластеров следующим образом [2]:

$$ N_ {T} (n) =\ alpha n ^ {3} + \ frac {1} {2} \ beta n ^ {2} + \ gamma n + 1 ~~ n \ ge {0} $$ ( 6)

где N _Т ( нет ) - общее количество атомов, а

$$ \ alpha =C / 6 $$ (7)

где C - количество тетраэдрических ячеек, на которые разбивается многогранник, и

$$ \ beta =1 / 2F_ {s} $$ (8)

где F _s - количество треугольных граней на поверхности, и

$$ \ gamma =F_ {s} / 4 + V_ {i} + 1-C / 6 $$ (9)

где V _я - количество вершин внутри. Они также показывают, что

$$ N_ {S} (n) =\ beta n ^ {2} + 2 ~~ n \ ge {1}; ~~ N_ {S} (0) =1 $$ (10)

и

$$ N_ {I} (n) =N_ {T} (n) - N_ {S} (n), $$ (11)

где N _Я ( нет ) - количество внутренних атомов. Эта информация (уравнение (11)) содержится в матрице смежности, а также в уравнениях. (3, 4, 5). Эти уравнения являются проверкой результатов на основе данных матрицы смежности. Для центрированных многогранников мы также имеем

$$ N_ {I} (n) =N_ {T} (n-1), $$ (12)

и из уравнения. (11) имеем

$$ N_ {T} (n) =N_ {S} (n) + N_ {S} (n-1) + ... + N_ {S} (1) + N_ {S} (0). $$ (13)

Из этих уравнений мы можем вывести магические формулы для каждого из кластеров следующим образом. После вычисления топологической (0,1) -матрицы сопряжения A для кластера с n оболочки, как описано, мы знаем, что ее размер N = N _Т ( нет ) указывает общее количество атомов. Сумма записей в столбце i дает количество облигаций c нет _я ( нет ) для атома i и подсчитывая количество сумм столбцов, равное c нет _я ( нет ) дает, очевидно, \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \). Поскольку мы знаем, что они зависят от n как многочлен степени не выше 3, мы можем вычислить N _Т ( нет ) и c нет _я ( нет ) для 4 последовательных значений n , скажем н = n ₀ + j , j =0,1,2,3. Тогда простой интерполирующий полином даст коэффициенты полинома. Необходимо проверить, что, увеличивая n ₀ , который обычно равен 1, формулы не меняются. Если формулы становятся устойчивыми с n ₀ on, то они сохраняются для всех n ≥ n ₀ . В некоторых случаях полиномиальное соотношение выполняется только для четных n значения или нечетные. Например, для ромбического додекаэдра с ГЦК (таблица 1) последовательные оболочки имеют восемь атомов с координацией 3, когда n ≥2 четно, и нет, если n странно. В таких случаях для n будут выполняться разные полиномиальные соотношения. четный и n странно, но данные используются для n = n ₀ + j , j =0,2,4,6 с n ₀ нечетное (например, n ₀ =1) или n ₀ даже ( n ₀ =2). Чтобы получить точные рациональные коэффициенты, необходимо решить систему Вандермонда для коэффициентов в точной арифметике, используя символический набор инструментов MATLAB. Вот как вычисляются таблицы 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 и 19. В следующем разделе мы определим магические формулы для N _Т ( нет ), N _B ( нет ), так и для \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) по запрещенному рецепту.

Дисперсия (экспонированная доля, FE) поверхностных атомов определяется как:

$$ \ text {FE} =\ frac {N_ {S}} {N_ {T}} \ cdot 100 \% $$ (14)

где N _S - количество поверхностных атомов, а N _Т - полное количество атомов [9]. Мы можем сравнивать разнородные кластеры, определяя относительный размер кластера как:

$$ d_ {rel} =b (N_ {T}) ^ {1/3}; ~~ b =d_ {at} ^ {- 1} \ cdot \ left (\ frac {6V_ {u}} {\ pi n_ {u}} \ right) ^ {1/3} $$ (15)

где d _в ковалентный диаметр атома, V _u - объем элементарной ячейки, а n _u - количество атомов в элементарной ячейке. Константа кристаллической структуры b равно 1,105 для ГЦК- и ГПУ-кластеров, 1,137 для ОЦК-кластеров [1], 1,488 для простых кубических кластеров и 1,517 для кубических кластеров алмаза. Как показано выше, формула для FE представляет собой отношение квадратичного к кубическому для кластеров и может быть смоделирована аппроксимацией кривой степенного закона по сравнению с d _rel . Переменная d _rel позволяет сравнивать разные кластеры друг с другом безотносительно кристаллической структуры. Для некоторых платоновых кластеров, где нет элементарной ячейки кристалла, мы используем \ (N_ {T} ^ {1/3} \) в качестве переменной.

Результаты и обсуждение

Изучение размера и формы металлических нанокластеров развивалось с момента зарождения два десятилетия назад. В таблице 20 показан некоторый прогресс по состоянию на 2018 год.

В таблице мы перечисляем в первую очередь переходные металлы, а не сплавы или соединения, за исключением усеченной гексагональной бипирамиды, где только Fe ₂ О ₃ был найден. Кластеры золота были синтезированы больше, чем любой другой элемент, из-за его свойств и стабильности. В следующих подразделах мы ограничиваем наше обсуждение конкретными темами, связанными с магическими формулами и типами кластеров.

Кластеры Федеральной комиссии по связи

Восемь переходных металлов кристаллизуются в структуре ГЦК, см. Таблицу 21 ниже, включая плазмонные благородные металлы и важные каталитически активные элементы. Подавляющее большинство синтеза нанокластеров было связано с этими элементами. Ссылки на синтез ГЦК элементов различных форм и размеров приведены в Таблице 21.

Сплавы этих элементов также представляют интерес, но ссылки на них слишком многочисленны, чтобы приводить их здесь. Часто общие синтезируемые формы представляют собой кубы, октаэдры, кубооктаэдры и икосаэдры. Обычно кластеры с гранями (111) синтезировать легче, поскольку поверхность (111) обычно имеет меньшую энергию, чем поверхность (100) [7]. Мы находим для ГЦК ромбического додекаэдра, что существуют четные и нечетные формулы. Они согласуются с [1], если заменить « n ”В наших четных формулах на 2 ( m −1). Формулы для кубооктаэдров с ГЦК, перечисленные в [24], дают те же магические числа, что и наши, но сдвинуты на 1, поскольку они нумеруют оболочки как n =1,2,… и мы используем нумерацию n =0,1,…. Наши магические формулы согласуются с формулами в [2, 4], и из уважения к ранее опубликованным работам и для сохранения преемственности математики мы используем обозначения [2, 4]. Ниже представлены 5 форм кластера fcc и связанные с ними магические формулы.

Кластеры скрытых копий

Семь переходных металлов в периодической таблице имеют ОЦК структуру, см. Таблицу 21. Из магнитных элементов Fe, Co и Ni только железо имеет ОЦК. Нанокубы железа, по-видимому, являются единственной полученной формой кластера ОЦК [25]. Хотя объемная структура железа является ОЦК, были синтезированы ГЦК нанокластеры [26]. В этой ссылке также анализируется термодинамическая стабильность кластеров. Здесь мы представляем 5 форм кластера скрытой копии и связанные с ними магические формулы.

Кластеры HCP

Двенадцать переходных металлов имеют структуру ГПУ, см. Таблицу 21. Однако многие из них окисляются или не имеют убедительного научного интереса к синтезу. Что касается гексагональной бипирамидальной формы кластера в таблице 11, кластеры золота были синтезированы [27]. Родственная усеченная гексагональная бипирамида, по-видимому, была образована только α -Fe ₂ О ₃ [28].

Платонические кластеры

Платоновы тела были известны еще со времен древних греков. К ним относятся куб, тетраэдр, октаэдр, икосаэдр и додекаэдр. В предыдущих таблицах мы перечислили магические формулы для кубов и октаэдров fcc и bcc. Здесь мы перечисляем формулы для икосаэдра, додекаэдра, тетраэдра и объемно-центрированного тетраэдра. Как упоминалось ранее в разделе «Методы», додекаэдр уникален для кластеров, анализируемых здесь, в этом c нет _s =7 относится как к поверхностным, так и к объемным атомам. На рис. 1б мы показали, что внешняя оболочка содержит как пяти-, так и шестикоординированные атомы. Когда оболочка становится внутренней, эти пяти- и шестикратно скоординированные атомы становятся семи- и восьмикратно скоординированными со связями с оболочкой с обеих сторон. Кроме того, шестикратно скоординированные атомы внешней оболочки имеют семикратную координацию, связываясь с внутренней оболочкой. Таким образом, додекаэдр состоит из семичастных атомов с поверхностной и объемной координацией. Каждая оболочка в структуре имеет 12 атомов пятичленной оболочки, которые производят 12 n −12 объемных семикоординированных атомов. Остальные члены семеричной координации - это поверхностные атомы.

Было показано, что нанокластеры золота принимают платоновую форму [29]. Эта ссылка включает куб, тетраэдр, октаэдр и икосаэдр. Позднее был синтезирован нанокластер золотого додекаэдра [30]. Здесь мы показываем оба правильных тетраэдра, которые «похожи на ГЦК» в этом c _M =12, как в ГЦК-структурах, и объемно-центрированный тетраэдр в Таблице 16, где зеленые атомы имеют одинарные связи. Формулы платонической магии представлены ниже.

Кластеры алмазных кубов, простых кубов и декаэдров

Элементы кремний и германий имеют алмазную кубическую решетку, а также алмазный аллотроп углерода. В частности, в последнее время вызывает интерес кремний с концевыми водородными группами. Было установлено, что поверхность (100) с концевым водородом, приводящая к кубической форме кластеров, имеет самую низкую энергию [31]. Осуществлен синтез нанокубов Si-H размером 8−15 нм [32]. В таблице 17 показана диаграмма кластеров Si-H с концевыми водородными группами, с одинарными атомами водорода, выделенными зеленым цветом. Если нанокластер принимает кубическую форму алмаза, будут одиночные оборванные связи, которые необходимо пассивировать, чтобы сохранить структуру. Глядя на магические формулы, мы предполагаем, что состав таких кластеров Si-H равен \ (\ phantom {\ dot {i} \!} \ Text {Si} _ {8n ^ {3} + 6n ^ {2} -9n +5} \ text {H} _ {12n-8} \), где n - количество оболочек в кластере. Такие полупроводниковые квантовые точки могут представлять интерес с точки зрения оптических свойств, и было определено, что изменение ширины запрещенной зоны в зависимости от размера кластеров с водородной границей обратно пропорционально размеру кластера [33].

Простая структура кубической решетки ранее анализировалась другими авторами [4], хотя и без подробностей, которые мы приводим. Ранее мы изучали d -мерные формы гиперкуба [14]. Полоний - единственный элемент, имеющий простую кубическую структуру. Он радиоактивен, поэтому его можно использовать в специализированных приложениях. Здесь мы представляем формулы магии алмазного кубического, простого кубического и декаэдрического кластеров.

Магические топологические формулы

Измеренная структурная сложность кристаллов может дать нам представление о простоте или сложности структуры, а правильное использование может ранжировать соответствующие структуры. Для такого ранжирования полезно рассмотреть графическое описание кристаллической решетки, как упомянуто в разделе «Методы». Топологическая сложность кристаллических структур измеряется распределением вершин графа, I _vd [34], с использованием программного обеспечения ToposPro, версия 5.3.2.2 [35]:

где a _я степень (согласованность) i -й вершине и суммирование продолжается по всем v вершины фактор-графа. В этом параметре используется бесконечный кристалл, а не кластеры, которые мы рассматривали, но он полезен для измерения относительной сложности различных кристаллических структур. Таким образом, чем больше число или больше информации на графике, тем он сложнее. В Таблице 22 мы показываем значения I _vd полученный из ToposPro, полученный из файлов cif для кристаллических структур в открытой кристаллографической базе данных. Полоний - единственный элемент, который кристаллизуется в простой кубической структуре, и его значение равно нулю, то есть фактор-граф имеет одну вершину и ноль ребер, что согласуется с тем, что мы ожидаем, что простая кубическая структура действительно является наименее сложной структурой. Также показана соль NaCl с двумя элементами в простой кубической структуре, а также кремний в кубической структуре алмаза, золото в ГЦК, железо в ОЦК и кобальт в ГПУ-структурах. Мы упоминаем, что другая мера сложности, связанная с энтропией Шеннона [34], бесполезна, потому что эта мера для всех элементов тождественно равна нулю.

Аналогичный метод, описанный в разделе «Методы» для определения магических формул, может быть применен к магическим формулам, описывающим топологические индексы. Только здесь степени многочленов равны 7, 8 или 9, поэтому их значения не менее 10 последовательных n -значения необходимо вычислить. Тогда результат дает интерполяционная задача более высокой степени. Поскольку решение линейной системы размером 10 × 10 с помощью символьного набора инструментов требует некоторого времени, все коэффициенты для топологических индексов могут быть вычислены одновременно с использованием нескольких правых частей, чтобы получить коэффициенты всех многочленов.

Магические формулы для топологических индексов подробно описаны в таблицах 23, 24 и 25. Четыре индекса, которые мы анализируем, зависят только от n , количество оболочек в кластере. Глядя на результаты, простая кубическая решетка как наименее сложная структура также имеет «простейшие» формулы. Несмотря на наши усилия, мы не можем найти индекс Сегеда для кубов bcc. Стабильного решения не найдено. В общем случае ГЦК-структуры легче решать для топологических формул. Нам не удалось решить ни одной ГПУ-структуры, а только несколько ОЦК-структур. Это может быть связано с топологической сложностью, поскольку ГЦК-решетка проще, чем ОЦК или ГПУ, см. Таблицу 22. В таблицах мы приводим формулы для кубооктаэдра, икосаэдра и декаэдра. Ранее мы [12] предоставили таблицы числовых данных для этих индексов с оговоркой, что кубооктаэдр в [12] имеет разные магические числа. Здесь мы видим, что табличные данные можно кратко резюмировать в виде волшебных формул. Также степень полинома индекса следует правилам из трехмерного пространства [14]. Некоторые топологические индексы для Платоновых тел были опубликованы ранее [36]. По этой ссылке мы проверяем индекс Винера для всех пяти твердых тел для n =1. Индекс Винера для рядов элементарных ячеек ГЦК-решетки изучался [37], но наши результаты нельзя сравнивать, так как мы изучаем кластеры.

Дисперсия

Процент поверхностных атомов (дисперсия, FE) различных кластеров представлен на рис. 2. Известно, что нанокластеры платины обладают каталитической активностью по отношению к реакции восстановления кислорода (ORR), которая зависит от размера и формы [38]. В этой ссылке установлено, что кубооктаэдрические кластеры платины размером 2,2 нм обладают максимальной активностью ORR. Также известно, что для сплавов PtNi поверхность (111) является предпочтительной для ORR [39]. Мы сравниваем икосаэдрические, октаэдрические, декаэдрические и кубооктаэдрические кластеры для FE при d _rel =7,5 для платины при 2,2 нм. Икосаэдрические, октаэдрические и декаэдрические кластеры имеют поверхности с гранями (111). Используя степенные законы на рис. 2, находим для заданного d _rel что КЭ для икосаэдрических кластеров составляет 47,9%, для кубооктаэдрических 52,8% и для декаэдрических 57,5%, и что для октаэдрических кластеров FE =58,9 % . Таким образом, по форме октаэдрические кластеры имеют как поверхность (111), так и самое высокое значение FE для аналогичного размера. Как коэффициент степенного закона, так и показатель степени важны для определения FE при малых d _rel . Математическая интерпретация показателя степени закона дает физический смысл как отношение ординаты FE к абсциссам d _rel , или относительное процентное изменение FE к относительному процентному изменению d _rel . Коэффициент степенного закона - это просто значение FE, когда d _rel =1.

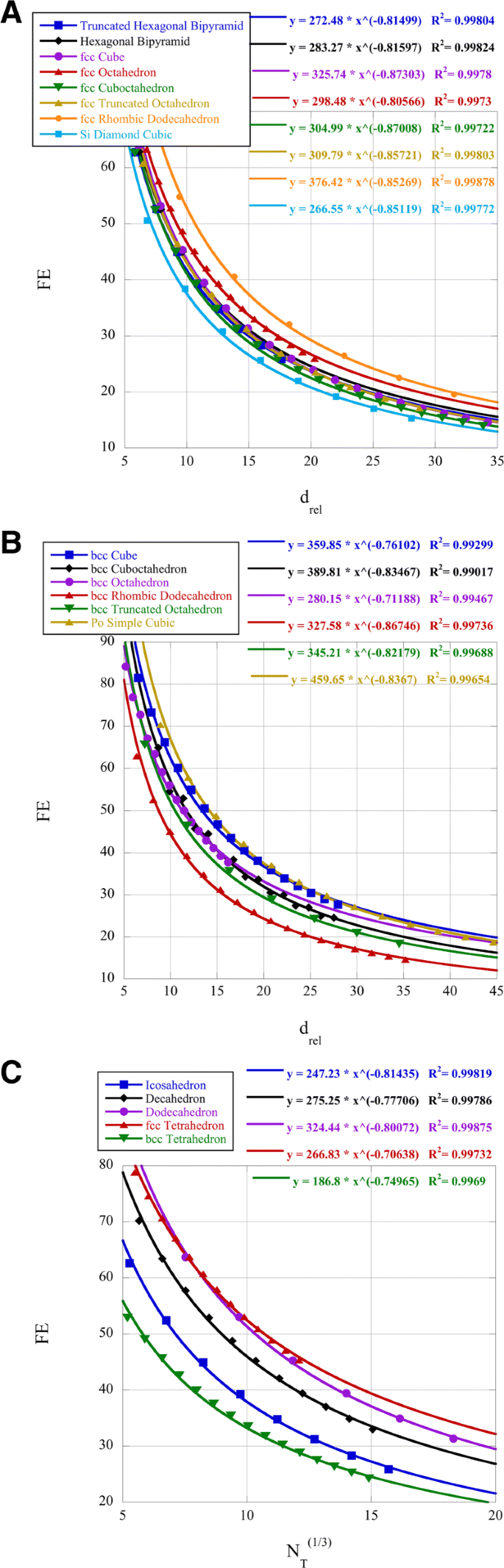
Дисперсия КЭ для нанокластеров

Другая группа исследователей синтезировала икосаэдрические кластеры из сплава платины и сравнила активность с октаэдрическими [40]. Эти нанокластеры имели размер около 13 нм или N =20 000 для октаэдрических кластеров и N =15000 для икосаэдрических кластеров. Это дает d _rel =30 для октаэдрических кластеров и 25 для икосаэдрических кластеров. Используя соответствующие степенные законы, это дает FE =18,0 % для октаэдрических и 19,8% для икосаэдрических кластеров. Существует очень небольшая разница в FE для этого размера кластера, но икосаэдрический кластер имеет значительную степень деформации из-за двойникования, которое может сдвигать центр d-полосы, таким образом влияя на результаты ORR [40]. Однако, учитывая данные [38], зависящие от размера, можно предположить, что кластеры меньшего размера будут давать еще более высокие данные ORR. Действительно, 4 нм Pt ₃ Октаэдры Ni, легированные Mo, дали рекордные результаты ORR [41].

Выводы

Мы изучили 19 типов нанокластеров и некоторые соответствующие магические формулы для числа атомов, связей, координационных чисел и топологических индексов. К ним относятся кластеры с ГЦК, ОЦК, ГПУ, Платоновы твердые тела, алмазные кубические, простые кубические и декаэдрические кластеры. Большинство из этих результатов более подробны, чем было определено ранее, и большое количество перечислено впервые. Грандиозная цель исследований в области материалов - это соотношение структуры и свойств. Это подробное исследование магических взаимоотношений нанокластеров является шагом в этом направлении. Примером может служить обсуждение дисперсии поверхностных атомов и ее связи с каталитической активностью. Мы надеемся, что эти результаты помогут ученым в их исследованиях структуры нанокластеров и связанных с ними свойств.

Сокращения

скрытая копия:

объемно-центрированный кубический

cif:

файл с кристаллографической информацией

fcc:

гранецентрированный кубический

FE:

Экспонированная фракция, дисперсия

hcp:

гексагональный плотно упакованный

ORR:

Реакция восстановления окисления

rW (G):

Обратный индекс Винера

Sz (G):

Индекс Сегеда

W (G):

Индекс Винера

WW (G):

Индекс Гипер-Винера