Динамически настраиваемая прозрачность, индуцированная плазмонами, во встроенной в микросхему асимметричной волноводной системе на основе графена с нанорезонаторами

Фон

Плазмон-индуцированная прозрачность (PIT), которая представляет собой новое явление, аналогичное эффекту электромагнитно-индуцированной прозрачности (EIT), создающему резкое окно прозрачности в широком спектре поглощения [1], привлекла большое внимание из-за его потенциальных приложений в широком диапазоне такие поля, как медленный свет [2, 3], оптическое переключение [4], накопление света [5] и высокочувствительное зондирование [6, 7]. Устройства на основе PIT могут быть реализованы с ультракомпактными размерами из-за большой способности усиления локального поля и преодоления классического дифракционного предела света, обеспечиваемого поверхностными плазмонными поляритонами (SPP) [8, 9]. Было предложено множество конструкций для достижения эффекта PIT в плазмонных наноструктурах, включая системы связанных резонаторов [10,11,12,13], фотонно-кристаллические структуры [14,15] и структуры из метаматериалов [16,17]. Однако большинство этих структур, отображающих эффект PIT, практически невозможно настроить, если не изменить геометрические параметры структур, которые в значительной степени ограничивают активный контроль окон PIT и ухудшают качество.

Графен, монослой атомов углерода, расположенных в двумерной (2D) сотовой решетке [18], демонстрирует большой потенциал для разработки высокоэффективных оптоэлектронных устройств благодаря своим исключительным электрическим и оптическим свойствам, включая способность экстремального ограничения [19,20, 21], динамическая перестраиваемость и относительно низкие демпфирующие потери [22, 23]. В частности, поверхностная проводимость графена может динамически регулироваться химическим потенциалом через напряжение внешнего затвора или химическое легирование [24, 25], что делает графен перспективным кандидатом для создания настраиваемого PIT при фиксированных геометрических параметрах. Из-за этих необычных свойств по сравнению с обычными благородными металлами, был проведен широкий спектр исследований для реализации PIT на основе графена, таких как PIT-явления в графеновом волноводе, связанном с кольцевым резонатором [26, 27], и PIT-эффекты в графеновом волноводе. Волновод на основе наноленты на основе графена в сочетании с прямоугольной резонаторной структурой из графена [28, 29]. Sun et al. исследовали периодически структурированную двухслойную структуру графена, разделенную диэлектрическим слоем в терагерцовом диапазоне частот, где были получены мультиспектральные PIT-отклики [30]. Кроме того, настраиваемые эффекты PIT реализуются в периодически комбинируемых графеновых нанополосках и аналитически описываются с помощью модели связанного осциллятора Лоренца [31, 32]. Однако большинство предыдущих работ касалось графеновых резонаторов, связанных с однослойным графеном или системой волноводов из графеновых нанолент, а также графеновых нанополосковых систем с нормальным падающим светом. Исследований явления плазмонно-индуцированной прозрачности в листе графена с локально изменяющимися химическими потенциалами было очень мало или вообще не было исследований. Кроме того, по сравнению с нормальным падающим светом, плоское распространение имеет огромные преимущества для интеграции на кристалле.

На основании вышеупомянутых фундаментальных исследований в этой статье мы предлагаем плазмонную наноструктуру на основе графена, состоящую из плазмонного шинного волновода, соединенного сбоку с U-образной нанополостью, и прямоугольной нанополости на одном и том же монослое графена. Коммерческое программное обеспечение COMSOL Multiphysics, основанное на методе конечных элементов (МКЭ), используется для исследования передачи и электромагнитных характеристик наших конструкций. Результаты моделирования показывают, что явление PIT наблюдается в предлагаемой нами плазмонной наноструктуре. Кроме того, окно PIT может быть эффективно настроено путем изменения химических потенциалов нанополостей и волновода плазмонной шины. Кроме того, вводится теория связанных мод (CMT), чтобы объяснить особенности передачи явления PIT. Наконец, исследуется плазмонный датчик показателя преломления на основе предложенной плазмонной наноструктуры. Чувствительность измерения 333,3 нм / единица показателя преломления (RIU) достигается на пике пропускания PIT. Также реализован эффект медленного свечения с групповой задержкой более 1 пс. Предлагаемая новая плазмонная наноструктура может предложить новый способ реализации интеграции плазмонного устройства высокой плотности на основе графена на кристалле на монослое графена.

Методы

Для простоты предлагаемая структура моделируется подвешенным монослоем графена с локальным изменением химического потенциала для формирования соответствующего шинного волновода и нанорезонаторов. На рисунке 1а показаны схематическая конфигурация и геометрические параметры U-образной нанополости, непосредственно связанной с волноводом плазмонной шины. U-образный волновод, связанный с нанорезонаторами, с химическим потенциалом μ _c2 окружен таким же листом графена с химическим потенциалом μ _c1 . Ширина плазмонного волновода шины d составляет 20 нм. Ширина и высота U-образной нанополости составляют W _U =150 нм и L _U =120 нм соответственно. Точное теоретическое моделирование такой структуры требует трехмерных (3D) вычислений, что требует значительных затрат времени и памяти. Для решения этой проблемы метод эффективного показателя преломления использовался во многих публикациях [33,34,35], а показатель преломления структуры заменен эффективным показателем направленных мод, который определяется соотношением между постоянной распространения и волновое число в свободном пространстве. В нашей структуре лист графена рассматривается как ультратонкая пленка, которая характеризуется эффективным показателем, определяемым как n _eff = β / к ₀ , где k ₀ =2 π / λ - волновое число в свободном пространстве. Постоянная распространения β режима управляемого СПП, поддерживаемого однослойным графеном, записывается как [36, 37]

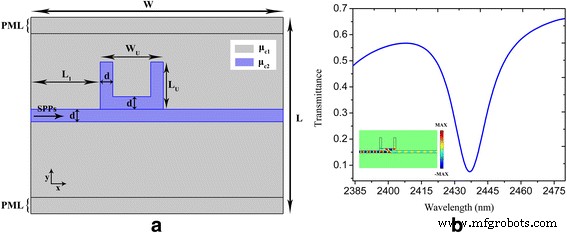
а, б Схематическая конфигурация и геометрические параметры U-образной системы волноводов с нанополостами и соответствующий спектральный коэффициент пропускания соответственно. вставка в б показывает электрическое поле ( E _y ) распределение на длине волны 2437 нм. Параметры установлены как W =800 нм, L =620 нм, d =20 нм, Вт _U =150 нм, L _U =120 нм, L ₁ =220 нм, τ =1 пс, μ _c1 =0,3 эВ и μ _c2 =0,9 эВ. Идеально подобранные слои ( PML ) шириной 50 нм реализованы на вершине и низ расчетной области для устранения нежелательных отражений от границы области

где μ ₀ и ε ₀ представляют проницаемость и диэлектрическую проницаемость вакуума соответственно, а μ _r и ε _r представляют собой относительную проницаемость и относительную диэлектрическую проницаемость соответственно. Поверхностная проводимость графена σ _g состоящий из межзонных электронных переходов σ _inter и внутризонное электрон-фотонное рассеяние σ _intra дается формулой Кубо [38, 39]

С

где μ _c - химический потенциал графена, ω угловая частота плазмона, ћ - приведенная постоянная Планка, e - заряд электрона, k _B постоянная Больцмана, T - температура, ℏ =h / 2 π - приведенная постоянная Планка, а τ - время релаксации импульса электрона. В частности, химический потенциал графена можно регулировать с помощью химического легирования или электрического стробирования [25, 26]. Михайлов и др. экспериментально показали, что плотность носителей в листе графена достигает 10 ¹⁴ см ⁻² была достигнута, что привело к химическому потенциалу 1-2 эВ при температуре ниже 250 К [40]. Кроме того, было продемонстрировано, что высококачественный подвешенный графен с подвижностью на постоянном токе достигает 10 ⁵ см ² V ^-1 s ⁻¹ может быть получено, что соответствует τ > 1,5 пс [41]. В этой статье время релаксации и химический потенциал, которые мы устанавливаем, достаточно консервативны, чтобы гарантировать надежность нашего численного исследования.

Результаты и обсуждение

Когда волна SPP проходит через U-образную нанополость с боковой связью, показанную на рис. 1а, энергия передается в нанополость. Глубокая впадина пропускания получается на резонансной длине волны из-за деструктивной интерференции между падающей волной и мощностью, уходящей из нанополости [12, 13]. На рисунке 1b показан спектр пропускания U-образной нанополости, напрямую связанной с плазмонным шинным волноводом с τ =1 пс, μ _c1 =0,3 эВ и μ _c2 =0,9 эВ. Выраженный провал с коэффициентом пропускания менее 0,1 достигается на резонансной длине волны 2437 нм. На вставке к рис. 1б показано соответствующее распределение электрического поля на резонансной длине волны, где видно, что плазмонный волновод почти не распространяется по плазмонному волноводу. На рисунке 2а показаны спектры пропускания с различным временем релаксации τ . =0,6, 0,8 и 1 пс, где видно, что более высокий контраст пропускания достигается при увеличении времени релаксации. Это объясняется уменьшением омического поглощения плазмонов при увеличении времени релаксации импульса электрона [39]. Расчетный коэффициент пропускания U-образной волноводной системы с нанорезонаторами для различных химических потенциалов μ _c2 представлен на рис. 2б. Время релаксации τ и химический потенциал μ _c1 постоянно поддерживаются на уровне 1 пс и 0,3 эВ соответственно. Можно видеть, что положение провалов динамически настраивается с помощью переменного химического потенциала нанополости и шинного волновода. Центральные длины волн провалов - 2455, 2445 и 2437 нм с μ _c2 =0,89, 0,895 и 0,9 эВ соответственно.

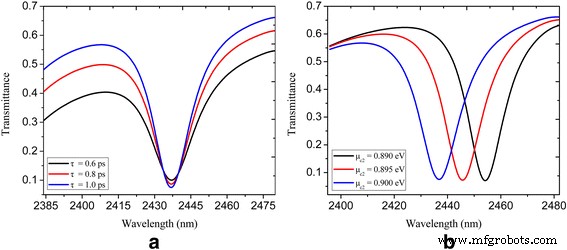
Спектральный коэффициент пропускания U-образной волноводной системы с нанорезонаторами, показанной на рис. 1: a с τ =0,6, 0,8 и 1 пс; μ _c1 =0,3 эВ; и μ _c2 =0,9 эВ; б с μ _c2 =0,89, 0,895 и 0,9 эВ; μ _c1 =0,3 эВ; и τ =1 шт.

Согласно CMT [12, 42, 43], спектральный коэффициент пропускания системы, поддерживающей резонансный режим с частотой ω ₀ можно записать как

где 1 / τ _я и 1 / τ _e представляют собой скорость затухания собственных потерь в нанополости и мощности, уходящей через волновод плазмонной шины, соответственно. Очевидно, минимальный коэффициент пропускания T _мин =(1 / τ _я ) ² / (1 / τ _я + 1 / τ _e ) ² может быть достигнуто, когда частота падающего света ω равна резонансной частоте ω ₀ . Поскольку 1 / τ _e намного больше 1 / τ _я можно получить провал пропускания, близкий к нулю, что хорошо согласуется с результатами моделирования.

Чтобы получить эффекты PIT, мы добавляем прямоугольную нанополость на основе плазмонной наноструктуры, показанной на рис. 1. Плазмонная наноструктура на основе графена, состоящая из волновода плазмонной шины, сбоку соединенного с U-образными и прямоугольными нанополостями, схематически показана на рис. . 3а. Между двумя нанорезонаторами существует сильная связь, когда они соединены через волновод плазмонной шины. Деструктивная интерференция между двумя резонансными путями возбуждения, связанными с U-образными и прямоугольными нанополостями, порождает явление PIT [10, 11]. Как показано на рис. 3b, резкий пик пропускания (увеличенный с 0,06 до 0,44) появился в запрещенной зоне пропускания, показанной на рис. 1b, что означает формирование окна PIT. Центральная длина волны окна PIT составляет 2437 нм, что в точности совпадает с местоположением центральной длины волны провала передачи, показанного на рис. 1b. Широкий резонанс U-образной нанополости разделен на две резонансные моды:одна с синим смещением, а другая с красным смещением [12, 13]. На рис. 3c – e показаны распределения электрического поля резонансных мод на длинах волн 2408, 2437 и 2457 нм соответственно. Мы можем видеть, что распределение электрического поля в нанорезонаторах синфазно с распределением электрического поля в волноводах плазмонной шины на длине волны 2437 нм, что означает, что падающий свет и свет, уходящий в волновод плазмонной шины из нанорезонаторов, сталкиваются с когерентным усилением. . Кроме того, распределения электрического поля показывают, что существует противофазность между нанополостями и плазмонным шинным волноводом на длине волны 2408 и 2457 нм, то есть соблюдены условия деструктивного резонанса, что приводит к подавлению прохождения волн [12].

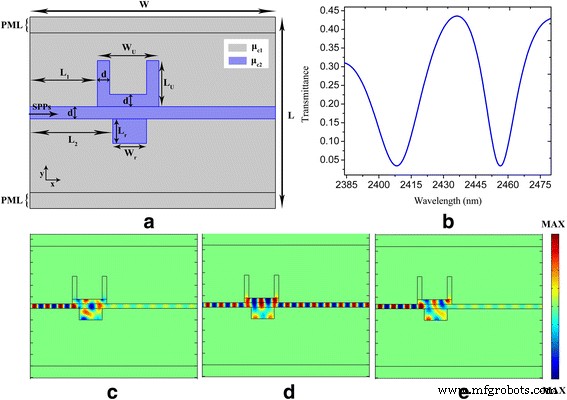
а, б Схематическая конфигурация и геометрические параметры U-образной и прямоугольной волноводных систем, связанных с нанорезонаторами, и соответствующий спектральный коэффициент пропускания соответственно. c - е Электрическое поле ( E _y ) распределение на длинах волн 2408, 2437 и 2457 нм соответственно. Параметры установлены как W =800 нм, L =620 нм, d =20 нм, Вт _U =150 нм, L _U =120 нм, L ₁ =220 нм, L ₂ =250 нм, L _r =50 нм, Вт _r =100 нм, τ =1 пс, μ _c1 =0,3 эВ и μ _c2 =0,9 эВ

Мы рассчитали спектральный коэффициент пропускания для U-образной и прямоугольной системы волноводов с плазмонной шиной, связанной с нанополостами, с варьируемым временем релаксации τ =0,6, 0,8 и 1 пс, а результаты показаны на рис. 4а. Видно, что контраст пропускания увеличивается с увеличением времени релаксации. Кроме того, динамическая настраиваемость окна PIT показана на рис. 4b. Химический потенциал μ _c1 постоянно поддерживается равным 0,3 эВ, а μ _c2 составляет 0,89, 0,895 и 0,9 эВ. Поскольку химический потенциал μ _c2 увеличивается, пик пропускания (на длинах волн 2452, 2445 и 2437 нм) в окне PIT явно смещен в синюю сторону. В результате в предлагаемой нами наноструктуре реализуется динамически настраиваемый эффект PIT за счет изменения химического потенциала нанополостей и плазмонного шинного волновода.

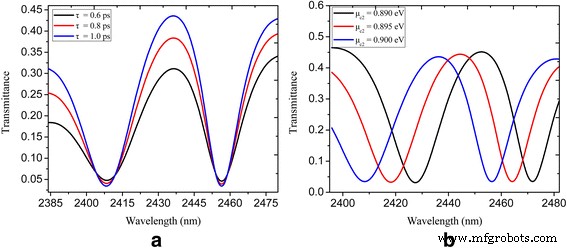
Спектральный коэффициент пропускания U-образной и прямоугольной волноводной системы с нанорезонаторной связью, показанной на рис. 3: a с τ =0,6, 0,8 и 1 пс; б с μ _c2 =0,89, 0,895 и 0,9 эВ

Чтобы исследовать, как геометрические параметры влияют на явление PIT, мы изменили расположение прямоугольной нанополости. На рисунке 5a показан спектральный коэффициент пропускания U-образной и прямоугольной системы волноводов с плазмонной шиной, связанной с нанополостой, где видно, что пик пропускания увеличился (увеличился с 0,44 до 0,52), а окно PIT становится шире с L ₂ возрастает в определенном диапазоне, что объясняется усилением силы связи между двумя нанополостями [11, 28]. Кроме того, мы обнаружили, что уменьшение ширины прямоугольной нанополости может привести к более высокому пику пропускания (увеличенному с 0,44 до 0,48), как показано на рис. 5b. Это предлагает еще один вариант настройки окна PIT. Коэффициент качества (Q-фактор) окон PIT определяется как λ ₀ / ∆ λ , где λ ₀ и ∆ λ - длина волны пика передачи и полная ширина на полувысоте (FWHM). В предлагаемой нами плазмонной наноструктуре достигается полуширина менее 30 нм и добротность около 80, что намного уже и выше, чем у аналогов PIT на основе графена, предложенных в вышеупомянутых ссылках [28, 29]. P>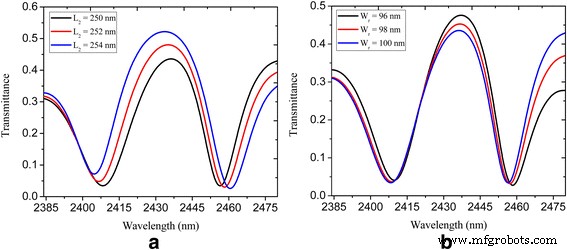

Спектральный коэффициент пропускания U-образной и прямоугольной волноводной системы, связанной с нанорезонаторами, показанной на рис. 3: a с L ₂ =250, 252 и 254 нм; б с W _r =96, 98 и 100 нм

В соответствии с CMT коэффициент пропускания в нашей плазмонной наноструктуре выражается как [12, 42]

$$ T ={\ left | \ frac {j \ left ({\ omega} _ {\ mathrm {U}} - {\ omega} _ {\ mathrm {r}} \ right) + \ gamma +1} { j \ left ({\ omega} _ {\ mathrm {U}} - {\ omega} _ {\ mathrm {r}} \ right) + \ beta + \ gamma +1} \ right |} ^ 2 $$ ( 6)

где γ и β обозначают коэффициент связи между двумя нанорезонаторами и коэффициент связи между нанорезонаторами и волноводом плазмонной шины соответственно. Мы можем обнаружить, что окно PIT может быть получено, когда резонансные частоты U-образной нанополости ω _U и прямоугольная нанополость ω _r примерно эквивалентны. Соответствующий пик передачи равен | ( γ + 1) / ( β + γ + 1) | ² .

На основе структуры, показанной на рис. 3a, мы создаем датчик показателя преломления, который реализуется путем изменения относительной диэлектрической проницаемости в формуле. 1. На рис. 6а показан спектральный коэффициент пропускания при различных показателях преломления n . , который относится к показателю преломления материала с недостаточной чувствительностью. Можно видеть, что длины волн пик / провал1 / провал2 сдвигаются от 2437,3 до 2457,3 нм / 2410,3 до 2432,4 нм / от 2457,3 до 2474,9 нм, когда показатель преломления n варьируется от 1 до 1,06. В качестве показателя преломления n увеличивается, и пик пропускания, и провалы демонстрируют красное смещение. Чувствительность датчика показателя преломления, определяемая как сдвиг длины волны пик / провал1 / провал2 на единицу изменения показателя преломления dλ / dn составляет 333,3, 368,3 и 293,3 нм / RIU соответственно. На рисунке 6b показаны пики и падения спектрального коэффициента пропускания с показателем преломления n . изменяется от 1 до 1,19, где мы можем видеть приблизительно линейную зависимость длин волн пиков / провалов от показателя преломления n .

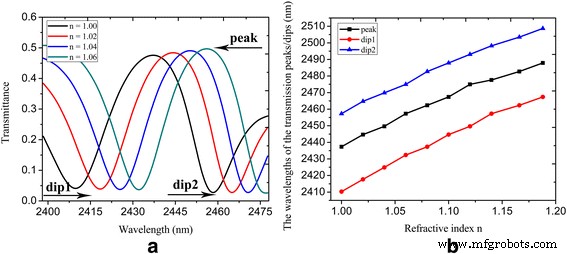
а Спектральный коэффициент пропускания с показателем преломления n =1, 1,02, 1,04 и 1,06; б длины волн пика / падения спектрального пропускания в зависимости от показателя преломления n . Параметры установлены как W =800 нм, L =620 нм, d =20 нм, Вт _U =150 нм, L _U =120 нм, L ₁ =220 нм, L ₂ =250 нм, L _r =50 нм, Вт _r =96 нм, τ =1 пс, μ _c1 =0,3 эВ и μ _c2 =0,9 эВ

Хорошо известно, что явление ПИТ сопровождается эффектом медленного свечения, вызванным резкой дисперсией [13, 29]. Эффект медленного свечения можно охарактеризовать групповой задержкой, выраженной как τ _g = ∂φ ( ω ) / ∂ ω где φ ( ω ) - эффективный фазовый сдвиг спектра пропускания. На рис. 7 показаны групповые задержки в окне PIT при различном химическом потенциале μ . _c2 . Вблизи пика пропускания PIT он предлагает большие положительные групповые задержки, указывающие на медленный световой эффект. Пиковые длины волн системы PIT при μ _c2 =0,89, 0,895 и 0,9 эВ составляют 2449,7, 2442,3 и 2434,7 нм соответственно, а соответствующие групповые задержки составляют 0,99, 1,1 и 1,02 пс соответственно. Таким образом, эффект медленного света эффективно настраивается путем изменения химического потенциала нанополостей и волновода плазмонной шины. Также следует отметить, что это экспериментальная статья. В действительности предлагаемая структура должна лежать на подложке, где показатель преломления больше, чем у воздуха, и частотная характеристика должна соответственно смещаться. Кроме того, ограничение плазмона выше, что сопровождается увеличением потерь, что приводит к уменьшению пикового значения окна прозрачности в спектре пропускания. Однако принцип такой же, как и в приостановленном случае.

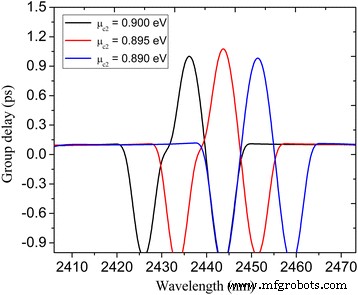
Группа задержек по сравнению с химическим потенциалом μ _c2 для графеновой PIT-системы, показанной на рис. 3а. Остальные параметры установлены как W =800 нм, L =620 нм, d =20 нм, Вт _U =150 нм, L _U =120 нм, L ₁ =220 нм, L ₂ =254 нм, L _r =50 нм, Вт _r =96 нм, τ =1 пс, μ _c1 =0,3 эВ