Параллельные R, L и C

Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:

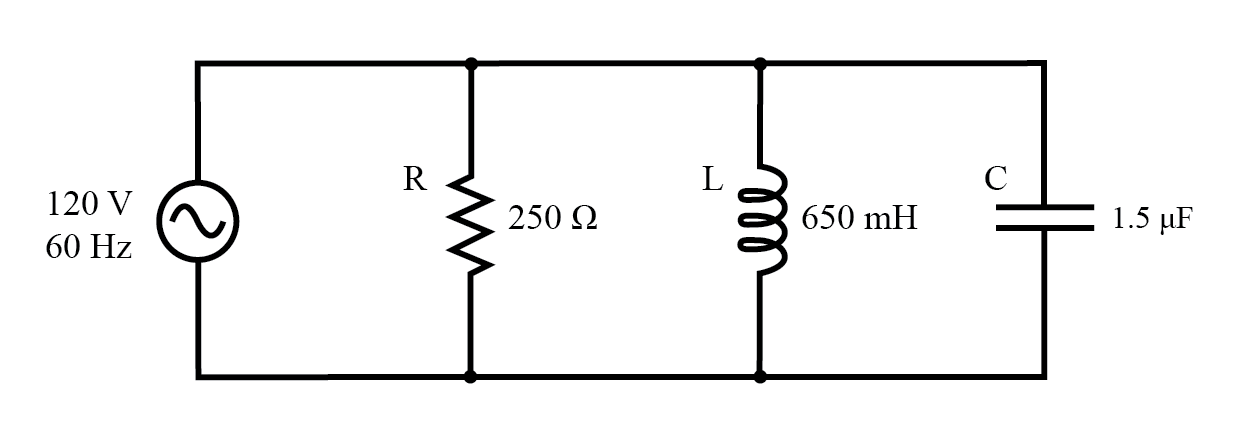
Пример параллельной схемы R, L и C.

Импеданс в параллельных компонентах

Тот факт, что эти компоненты подключены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.

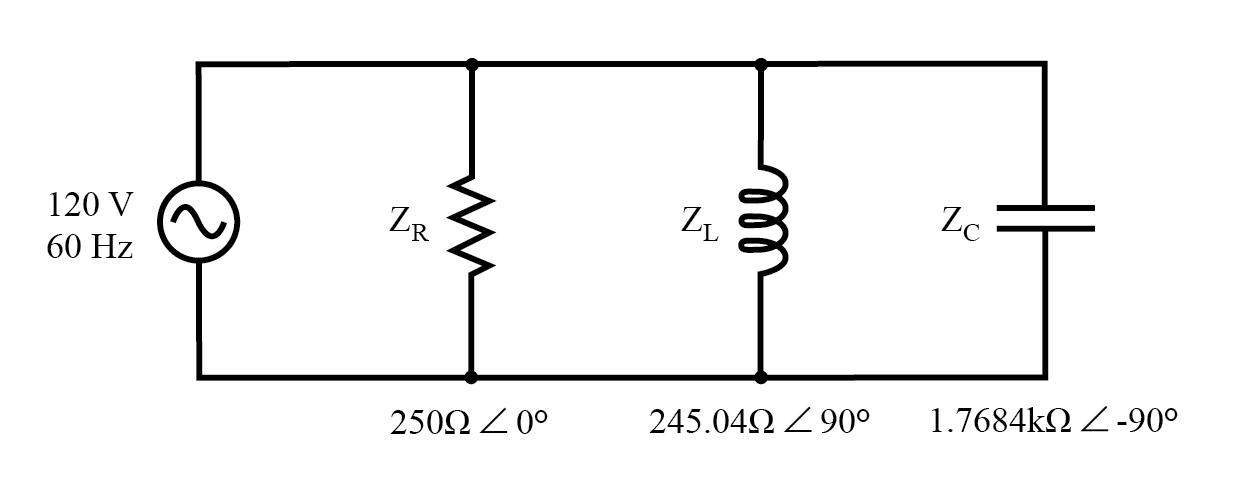
Пример параллельной схемы R, L и C с импедансами, заменяющими значения компонентов.

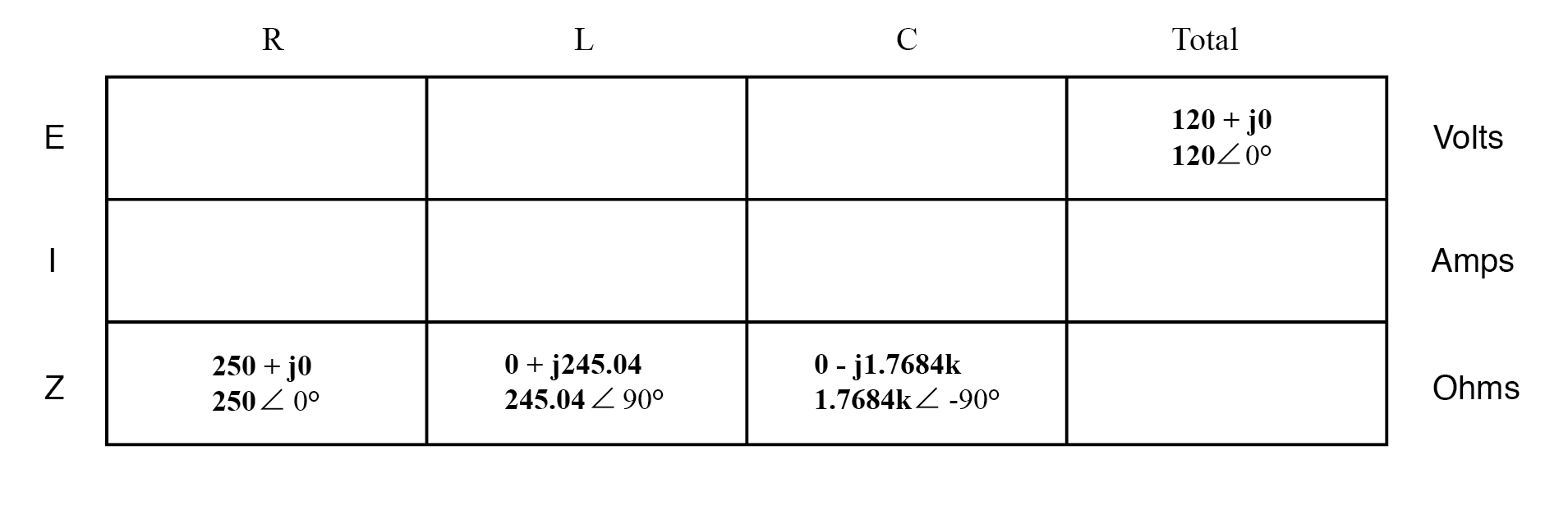
Со всеми значениями компонентов, выраженными в виде импедансов (Z), мы можем настроить таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуем правилам параллельных цепей вместо последовательного:

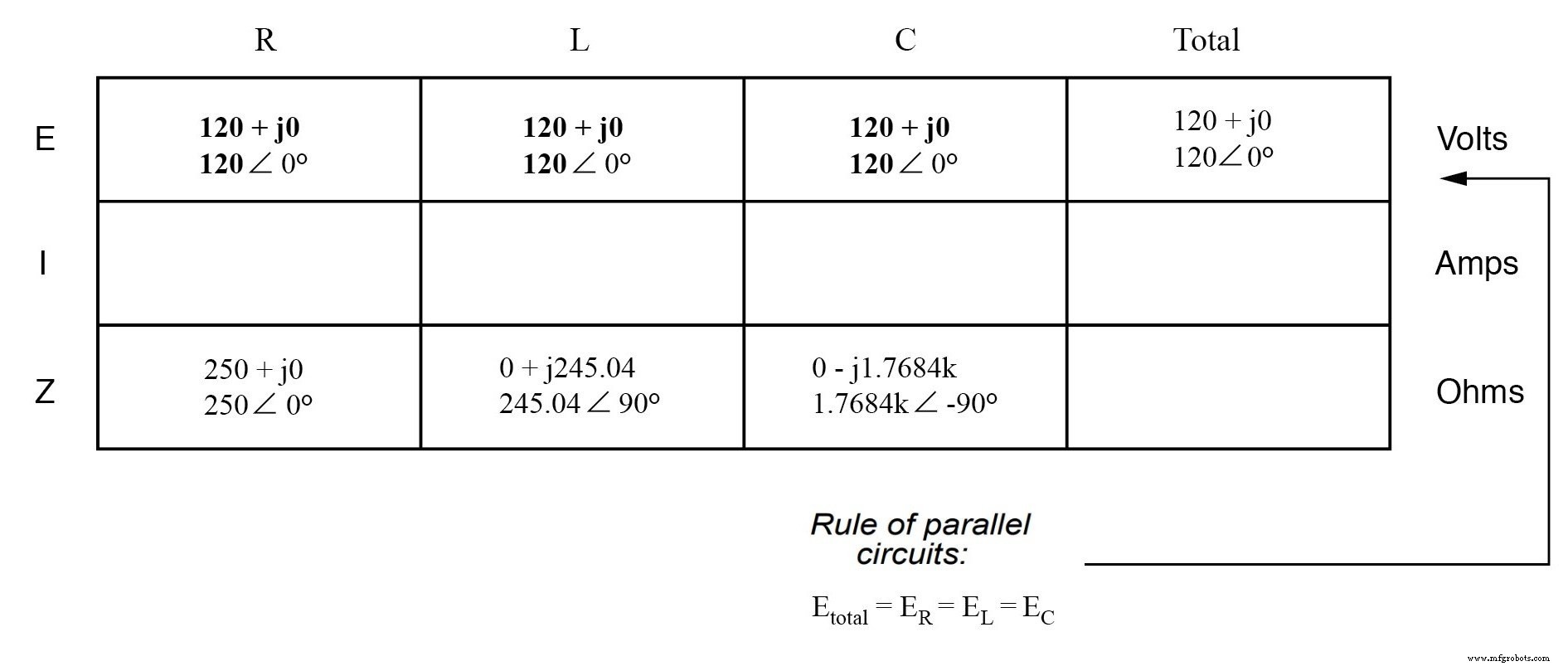
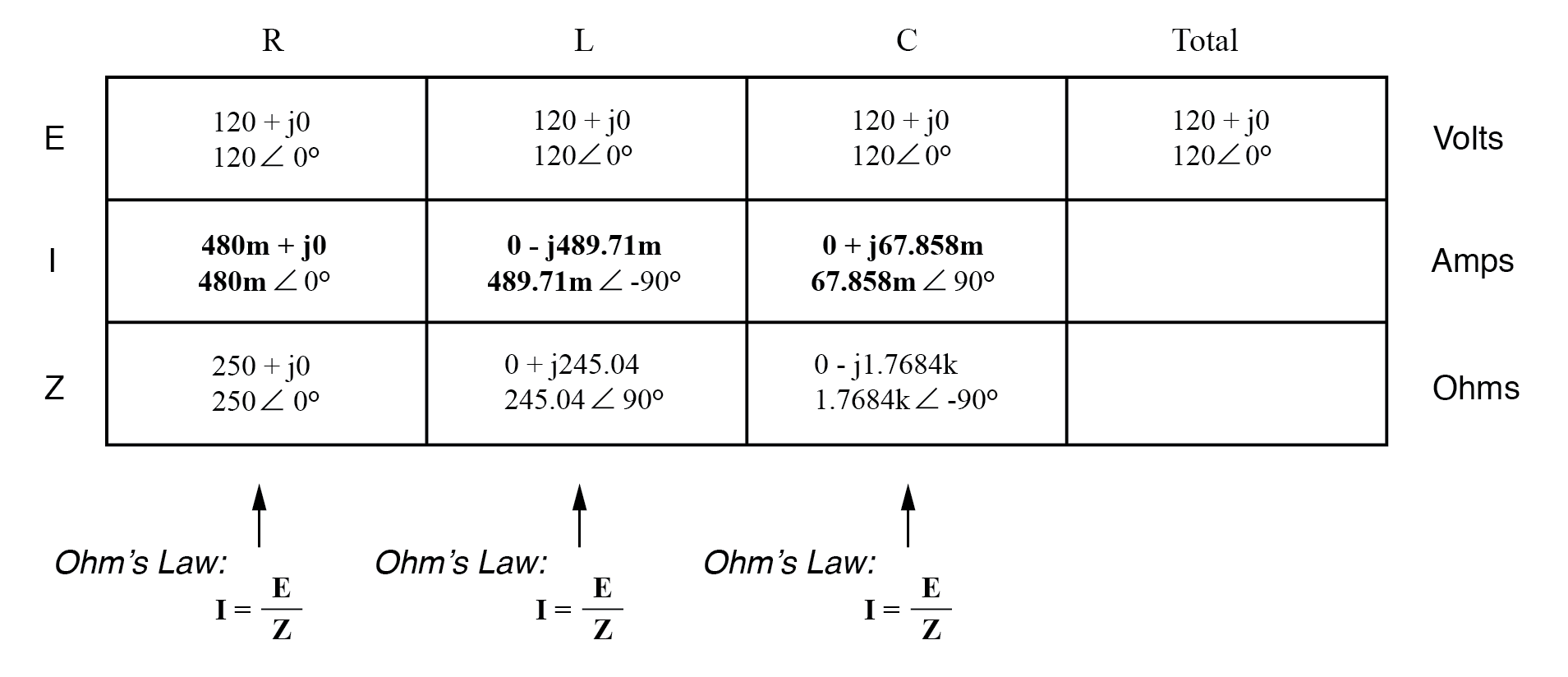
Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести цифру для общего напряжения во все столбцы компонентов в таблице:

Теперь мы можем применить закон Ома (I =E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:

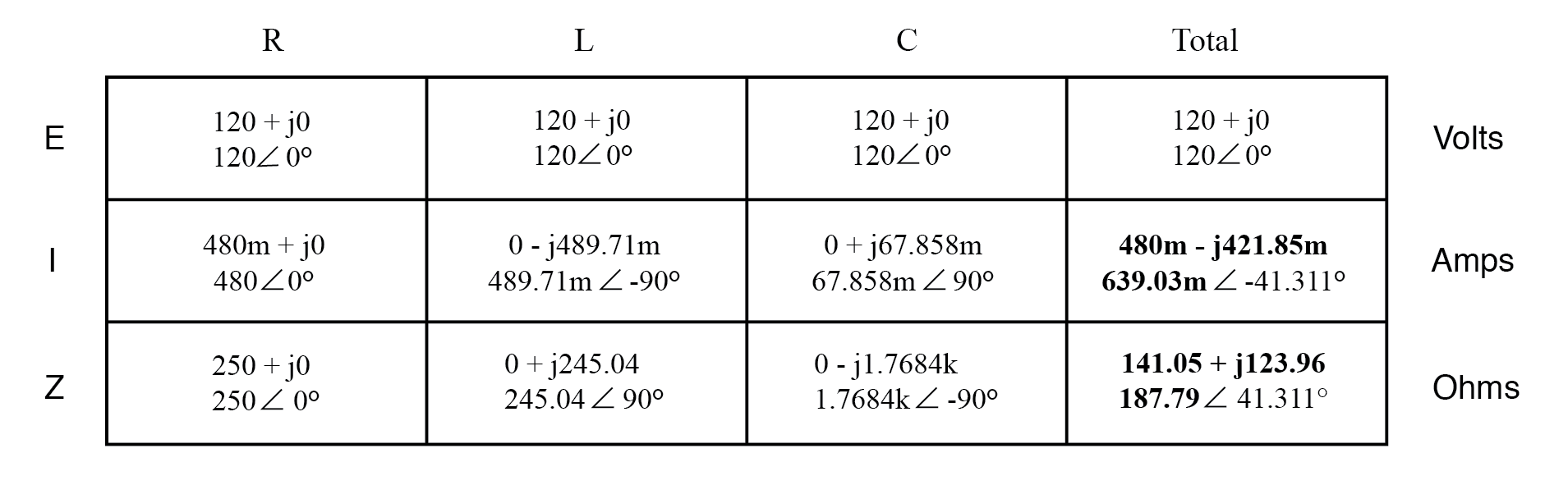
Расчет полного тока и полного импеданса

Есть две стратегии для расчета полного тока и полного сопротивления. Во-первых, мы могли рассчитать общий импеданс по всем отдельным параллельным импедансам (Z _Total =1 / (1 / Z _R + 1 / Z _L + 1 / Z _C ), а затем рассчитайте общий ток, разделив напряжение источника на полное сопротивление (I =E / Z).

Однако работа с уравнением параллельного импеданса с комплексными числами - непростая задача, учитывая все взаимные действия (1 / Z).

Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать индивидуальные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).

Второй способ вычисления общего тока и полного импеданса - сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи - переменного или постоянного тока - равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z =E / I).

Любой из этих методов при правильном применении даст правильные ответы. Давайте попробуем проанализировать эту схему с помощью SPICE и посмотрим, что произойдет.

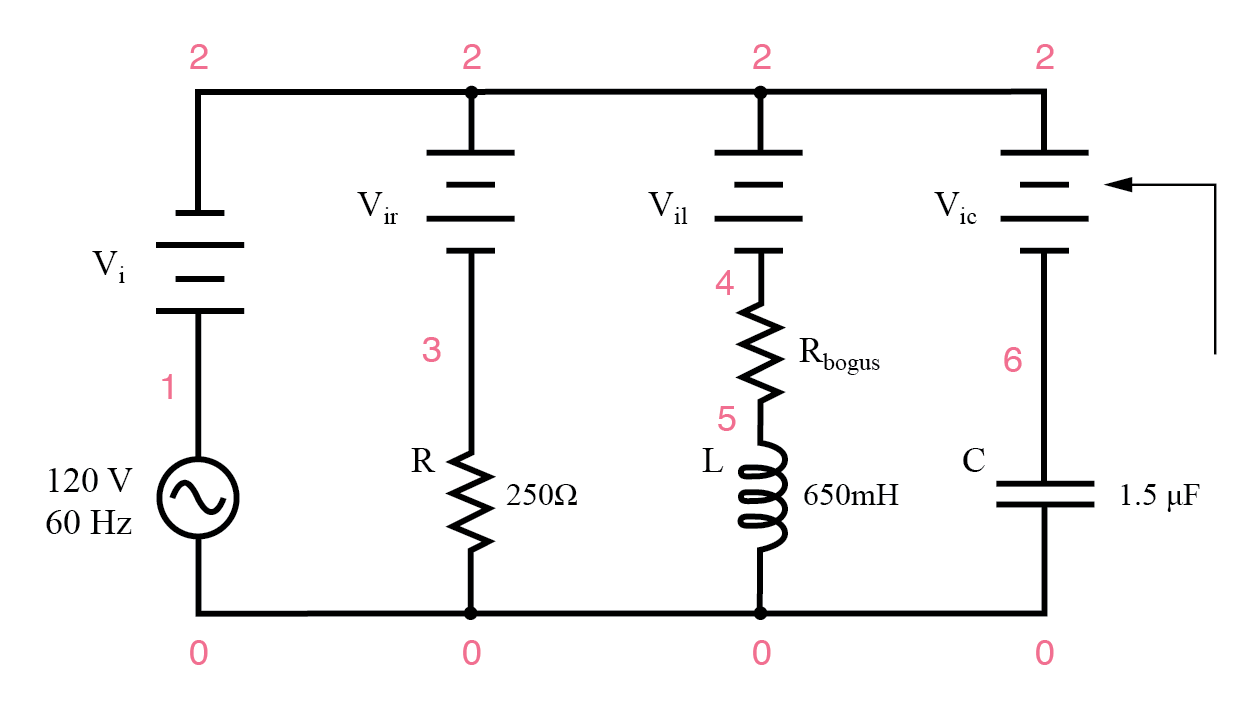
Пример параллельной схемы SPICE R, L и C. Символы батарей - это «фиктивные» источники напряжения, которые SPICE может использовать в качестве точек измерения тока. Все установлены на 0 вольт.

 цепь переменного тока r-l-c v1 1 0 ac 120 грех vi 1 2 ac 0 вир 2 3 ак 0 vil 2 4 ac 0 rbogus 4 5 1e-12 Vic 2 6 ac 0 г1 3 0250 l1 5 0 650м c1 6 0 1.5u .ac lin 1 60 60 .print ac i (vi) i (vir) i (vil) i (vic) .print ac ip (vi) ip (vir) ip (vil) ip (vic) .конец 

 freq i (vi) i (vir) i (vil) i (vic) 6.000E + 01 6.390E-01 4.800E-01 4.897E-01 6.786E-02 freq ip (vi) ip (vir) ip (vil) ip (vic) 6.000E + 01 -4.131E + 01 0.000E + 00 -9.000E + 01 9.000E + 01 

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Таблица последовательно-параллельных комбинированных цепей переменного тока