Логические правила для упрощения

Булева алгебра находит наиболее практическое применение при упрощении логических схем.

Если мы переведем функцию логической схемы в символьную (булеву) форму и применим определенные алгебраические правила к полученному уравнению, чтобы уменьшить количество членов и / или арифметических операций, упрощенное уравнение можно преобразовать обратно в форму схемы для логической схемы, выполняющей та же функция с меньшим количеством компонентов.

Если эквивалентная функция может быть достигнута с помощью меньшего количества компонентов, результатом будет повышенная надежность и снижение стоимости производства.

С этой целью в этом разделе представлены несколько правил булевой алгебры, которые можно использовать для приведения выражений к их простейшим формам.

Тождества и свойства, уже рассмотренные в этой главе, очень полезны для логического упрощения и по большей части имеют сходство со многими тождествами и свойствами «нормальной» алгебры.

Однако все правила, показанные в этом разделе, уникальны для логической математики.

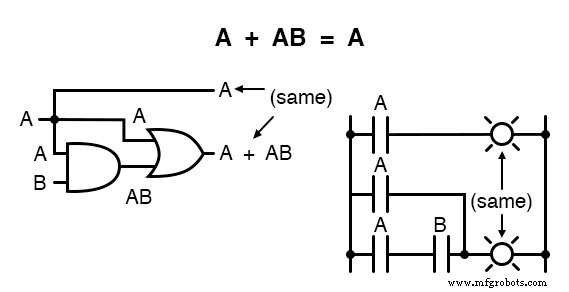
Это правило может быть подтверждено символически, если вычесть букву «А» из двух членов, а затем применить правила А + 1 =1 и 1А =А для достижения окончательного результата:

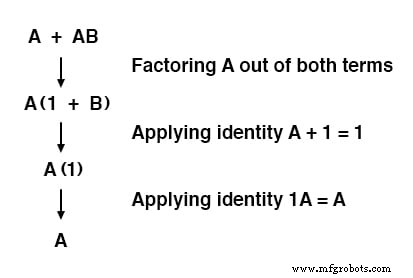
Обратите внимание, как правило A + 1 =1 использовалось для уменьшения члена (B + 1) до 1.

Когда такое правило, как «A + 1 =1» выражается буквой «A», это не означает, что оно применяется только к выражениям, содержащим «A».

В таком правиле, как A + 1 =1, буква «A» означает любую логическую переменную или набор переменных.

Это, пожалуй, самая сложная для новичков концепция логического упрощения:применение стандартизированных идентификаторов, свойств и правил к выражениям, не имеющим стандартной формы.

Например, логическое выражение ABC + 1 также сокращается до 1 с помощью тождества «A + 1 =1».

В этом случае мы понимаем, что термин «A» в стандартной форме идентификатора может представлять весь термин «ABC» в исходном выражении.

Следующее правило похоже на первое, показанное в этом разделе, но на самом деле оно сильно отличается и требует более умного доказательства:

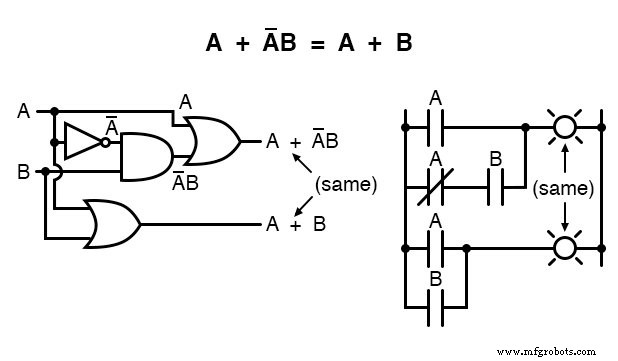
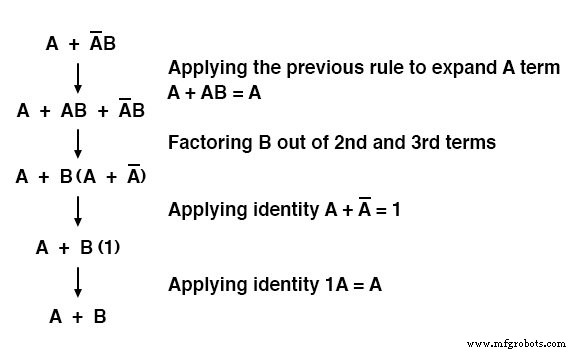
Обратите внимание, как последнее правило (A + AB =A) используется для «неупрощения» первого члена «A» в выражении, заменяя «A» на «A + AB».

Хотя это может показаться шагом назад, это определенно помогло свести выражение к чему-то более простому!

Иногда в математике мы должны делать «обратные» шаги, чтобы найти наиболее элегантное решение.

Знание, когда сделать такой шаг, а когда нет, является частью искусства алгебры, точно так же, как победа в шахматной партии почти всегда требует просчитанных жертв.

Другое правило включает упрощение выражения произведения сумм:

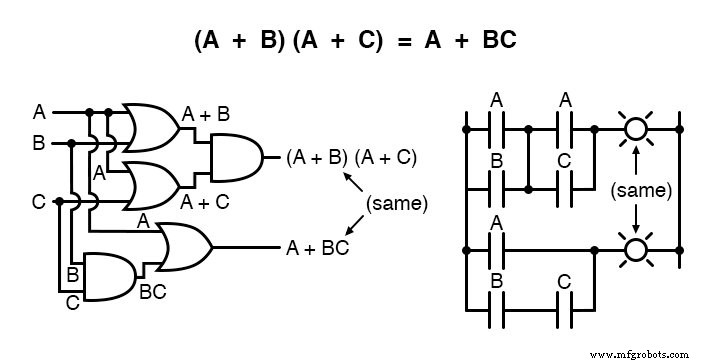
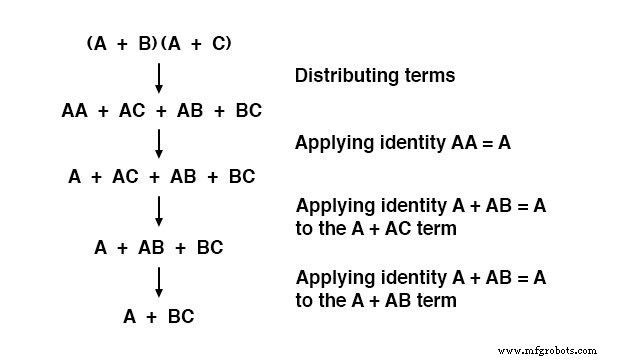
И соответствующее доказательство:

Подводя итог, вот три новых правила логического упрощения, изложенные в этом разделе:

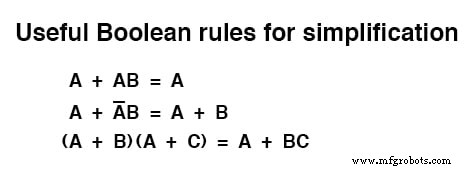
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист булевой алгебры