Аналитическая модель максимальной температуры канала в полевых МОП-транзисторах с Ga2O3

Фон

Оксид галлия (Ga ₂ О ₃ Полевые транзисторы на основе металл-оксид-полупроводник (MOSFET) являются отличными кандидатами для силовой электроники следующего поколения, в которых используются два основных преимущества Ga ₂ О ₃ :значительно большая ширина запрещенной зоны (~ 4.8 эВ) и высококачественные объемные кристаллы, получаемые с низкими затратами [1]. Огромные усилия были направлены на улучшение его электрических свойств во всех аспектах, таких как плотность тока [2], напряжение пробоя [3] и добротность мощности [4]. С экспериментальным подтверждением его беспрецедентного потенциала для силовых электронных устройств [5,6,7,8,9], теперь чрезвычайно важно изучить производительность и надежность Ga ₂ О ₃ МОП-транзисторы, такие как проблема самонагрева и, следовательно, максимальная температура канала ( T _макс ) из-за его относительно низкой теплопроводности ( κ , 0,11–0,27 Вт · см ⁻¹ К ^-1 при комнатной температуре) [1].

В последние годы появились различные методы оценки T _макс Га ₂ О ₃ МОП-транзисторы были предложены теоретически и экспериментально [10,11,12,13]. Как правило, численное моделирование позволяет количественно оценить T _макс определенного устройства. Однако это требует времени [14]. С другой стороны, извлечение T _макс экспериментально всегда недооценивается [15]. Следовательно, необходимо создать аналитическую модель, чтобы адекватно моделировать T _макс в Га ₂ О ₃ МОП-транзисторы, которые могут обеспечить достаточную точность с точки зрения эффективности времени и качественной оценки [14].

В этой статье мы предлагаем аналитическую модель T _макс для Ga ₂ О ₃ МОП-транзисторы с использованием преобразования Кирхгофа с учетом зависимости κ от температуры и кристаллографических направлений для Ga ₂ О ₃ . Предлагаемая модель может быть применена для Ga ₂ О ₃ МОП-транзисторы с естественной подложкой или подложкой с высокой теплопроводностью. Достоверность и точность аналитической модели методически проверяются путем сравнения с численным моделированием в COMSOL Multiphysics.

Методы и разработка модели

Аналитическая модель для T _макс в Га ₂ О ₃ Предлагаются полевые МОП-транзисторы на основе структуры, показанной на рис. 1. Основные параметры структуры перечислены в таблице 1. Фактически, было продемонстрировано, что джоулев нагрев сконцентрирован на краю стока затвора в Ga ₂ О ₃ МОП-транзисторы [13]. Чтобы упростить модель, предполагается, что эффект нагрева от затвора однороден [12] и может полностью проникнуть через оксид затвора из-за его незначительной толщины. Различные материалы подложки под Ga ₂ О ₃ канал рассматриваются в этой модели, например, объемный Ga ₂ О ₃ и высокий κ материалы, направленные на выполнимость и совместимость платы. Таким образом, устройство рассматривается как двухуровневая проблема. Подложка контактирует с идеальным радиатором, так что нижняя поверхность изотермична, а ее температура равна температуре окружающей среды ( T _amb , По умолчанию 300 КБ). На другой поверхности конструкции были наложены адиабатические граничные условия. Эти граничные условия можно резюмировать как [14, 16]

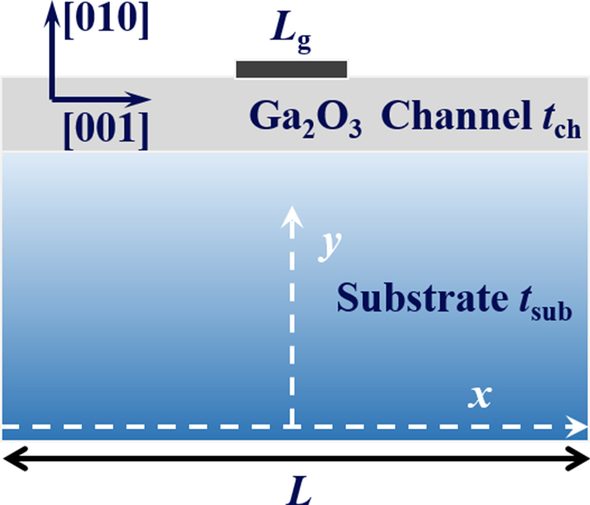
Принципиальная схема Ga ₂ О ₃ МОП-транзистор

где P , Т и κ _y обозначают плотность рассеиваемой мощности, температуру и теплопроводность в направлении [010] для Ga ₂ О ₃ , соответственно. Следует подчеркнуть, что единица измерения P в этой статье - Вт / мм.

κ значение Ga ₂ О ₃ , один из ключевых параметров тепловых характеристик материала, играет важную роль в распространении теплового эффекта, а также в точности модели. То есть подробное описание κ значение требуется из-за его серьезной анизотропии и температурной зависимости [17]. В общем, зависимость κ Га ₂ О ₃ по температуре ( T ) вдоль двух различных ориентаций кристалла ([001] и [010]) определяется как

Сравнительное исследование T _макс при разных P был выполнен COMSOL Multiphysics с учетом постоянного и реалистичного κ , соответственно. Мы обнаружили, что при P 1 Вт / мм, Т _макс получены значения 533 К и 622 К соответственно (не показаны). Следовательно, совершенно необходимо учитывать влияние T и кристаллографическое направление на κ Га ₂ О ₃ в модели.

Температурное поведение регулируется уравнением теплопроводности. Уравнение теплопроводности в установившемся режиме в Ga ₂ О ₃ домен

где κ _x обозначает теплопроводность направления [001] для Ga ₂ О ₃ . Уравнение нелинейной теплопроводности может быть решено с помощью преобразования Кирхгофа. Однако применение преобразования Кирхгофа может быть ограничено из-за сильно анизотропной κ в Га ₂ О ₃ , что справедливо, строго говоря, только для материалов с изотропными κ [14]. Учитывая указанное выше ограничение, не следует рассматривать κ _x и κ _y быть двумя независимыми переменными. На рисунке 2 показано соотношение между удельным тепловым сопротивлением, т. Е. 1 / κ , и T для направлений [001] и [010] на большом T диапазон соответственно. Видно, что 1 / κ _y можно заменить на 1 / ( cκ _x ) и c выбрано равным 1,64. Следовательно, уравнение. (6) можно преобразовать в следующее уравнение:

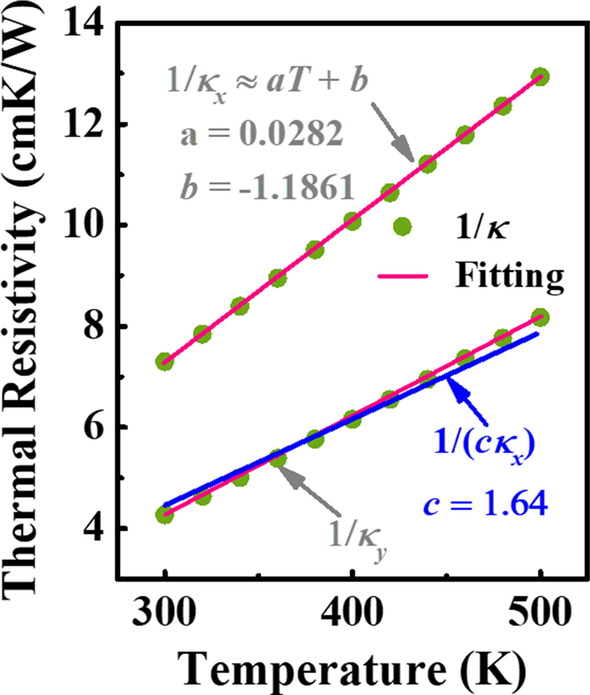
Связь между удельным тепловым сопротивлением и T для направлений [001] и [010]. Зеленые символы и красные линии обозначают фактические и подогнанные значения соответственно. Синяя линия представляет гипотезу 1 / κ _y ≈ 1 / ( cκ _x ), где c =1,64

На основе предыдущих приближений κ _x и κ _y преобразование Кирхгофа можно использовать без каких-либо ограничений. Кроме того, также видно, что величина, обратная κ ожидается, будет пропорционально T. Таким образом, чтобы уменьшить вычислительную сложность, выражение 1 / κ _x можно упростить как 1 / κ _x = АТ + b , как показано на рис. 2. Причина использования a , b и c просто удобство написания следующих уравнений.

Применяя преобразование Кирхгофа и метод разделения переменных, выражение T _макс можно получить как

где

Следует отметить, что S представляет собой сходящийся бесконечный ряд, и его приблизительное значение, которое можно легко получить, используется в расчетах вместо его фактического значения.

В случае Ga ₂ О ₃ МОП-транзисторы с высоким κ субстратов, преобразование Кирхгофа не может быть применено непосредственно теоретически. Фактически, чтобы преобразование было действительным, граничные условия должны быть либо изотермическими (константа T поверхность), либо иметь фиксированную плотность теплового потока. Однако из-за различного κ Га ₂ О ₃ и материал подложки, оба эти граничных условия не полностью выполняются при Ga ₂ О ₃ / подложка. Учитывая, что κ Га ₂ О ₃ намного ниже высокого κ подложка, гипотеза, изотермическая граница раздела Ga ₂ О ₃ и субстрат вводится. Эта гипотеза помогает получить выражение T _макс и его действительность будет проверена позже. В этом случае тепловое сопротивление ( R _TH ) высокого κ подложка, соотношение разницы между T _int и T _amb и PW , т.е. R _TH =( Т _int - Т _amb ) / ( PW ), можно рассчитать как R _TH = LW / ( κt _sub ), где W - ширина подложки [19]. Таким образом, выражение температуры Ga ₂ О ₃ / подложка ( T _int ) является

где κ _sub - теплопроводность гетерогенной подложки, которая считается постоянной. Кроме того, следует отметить, что тепловое сопротивление границы между Ga ₂ О ₃ и гетерогенные субстраты не включены в модель. Таким образом, с помощью уравнения. (8) выражение T _макс для Ga ₂ О ₃ МОП-транзисторы с гетерогенной подложкой могут быть получены как

где

Результаты и обсуждение

Обоснованность аналитической модели для T _макс в Га ₂ О ₃ В этом разделе проводилась систематическая проверка полевых МОП-транзисторов с учетом как собственной подложки, так и аналога с более высокой теплопроводностью. Лучший способ проверить достоверность модели - сравнить ее с экспериментальными данными. Однако некоторые ключевые геометрические параметры не могут быть найдены в экспериментальной литературе, например t _sub и L в исх. [12]. Поэтому моделирование методом конечных элементов, одно из наиболее точных средств, используется для проверки нашей модели. На рисунке 3 показана зависимость T _макс по удельной мощности P получено из COMSOL Multiphysics и аналитической модели для Ga ₂ О ₃ MOSFET с родной подложкой. Учитываются различные ключевые параметры, в том числе длина устройства L , толщина подложки t _sub , и температура окружающей среды T _amb . Как показано на рис. 3a, T _макс естественно увеличивается с увеличением плотности мощности, а скорость увеличения увеличивается с меньшим L . Это связано с тем, что устройство с большей L позволяет отвод тепла от активной области и, следовательно, его общая температура ниже, чем у меньшего L при том же P [11]. То есть его R _TH , наклон кривых меньше, чем у последнего . Кроме того, поскольку κ Га ₂ О ₃ будет уменьшаться с увеличением общей температуры, его R _TH также будет увеличиваться медленнее, чем при меньшем L следовательно, что очевидно на рис. 3а [19]. Аналогичным образом исследование зависимости T _макс на t _sub был выполнен, как показано на рис. 3b. Замечено, что тенденция T _макс относительно P такое же, как на рис. 3а. Чем тоньше субстрат, тем меньше подъем T . _макс по увеличенной плотности мощности, что понятно, что чем тоньше подложка, тем ниже общая температура, тем меньше R _TH и скорость его увеличения, как и анализ на рис. 3а. На рисунке 3c сравнивается влияние T _amb на T _макс как P увеличивается. Видно, что разница между двумя кривыми медленно увеличивается, в отличие от кривых на рис. 3а, б. Обычно R _TH преобладают геометрические параметры устройства и κ стоимость материала. Однако, учитывая, что в этом случае конструкция зафиксирована, увеличение R _TH индуцируется только уменьшением κ Га ₂ О ₃ . С другой стороны, наблюдается высокий уровень согласия для предложенной модели, которая учитывает T - и зависимые от направления отношения для κ Га ₂ О ₃ , что подтверждает масштабируемость модели. В среднем разница между предложенной моделью и симуляцией составляет <1 К. Наблюдаемое в целом отличное согласие предполагает, что предложенная модель является высокоэффективной и точной.

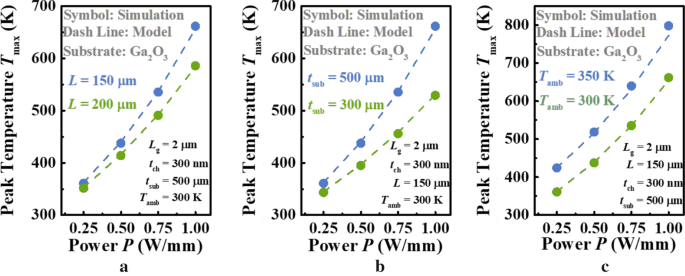
Зависимость T _макс на а длина устройства L , b толщина слоя подложки t _sub , и c температура окружающей среды T _amb на разной мощности P . Символы и линии обозначают результаты предложенной модели и моделирования соответственно

Аналогичным образом, как показано на рис. 4, аналогичные сравнения повторяются для Ga ₂ О ₃ МОП-транзисторы на высоком κ подложка, SiC. Здесь шаги для L и T _amb которые мы выбираем, больше, чем на рис. 3, и варьируемая толщина канала t _ch рассматривается вместо t _sub в таком случае. В противном случае разница между двумя кривыми T _макс относительно P на каждом рисунке будут неотличимы из-за эффективного рассеивания тепла подложкой SiC. κ SiC (3,7 Вт · см ⁻¹ К ^-1 ) применяется по умолчанию в программном обеспечении COMSOL Multiphysics. Благодаря высокому κ SiC, на всех рисунках хорошо видно, что увеличение T _макс приблизительно линейна как P увеличивается, а это означает, что влияние температуры на R _TH устройства незначительно. Следует отметить, что наша модель может успешно описать эту линейную зависимость. Однако очевидно, что T _макс Расчетная по текущей модели ниже, чем прогнозируется с помощью моделирования, и эта разница более очевидна с увеличением энергопотребления. Чтобы показать этот механизм, смоделировал T _int извлекаются с увеличением мощности и сравниваются с рассчитанным T _int по формуле. (10), как показано на рис. 5. Было обнаружено, что джоулев нагрев становится более концентрированным в середине устройства как P увеличивается. Есть 0,5 К и 4 К Δ T между моделью и симуляцией в этом месте, когда P =0,25 и 1 Вт / мм соответственно. Это причина того, что наша модель не может точно предсказать T _макс . Следовательно, более разумная гипотеза T _int необходимо для получения более высокой точности в будущем. Тем не менее, T _макс согласно прогнозам модели, будет всего на <4 К ниже, чем при моделировании, даже при плотности рассеиваемой мощности 1 Вт / мм. То есть, хотя гипотеза однородного T _int не соответствует действительности, наша модель может дать оценку T _макс с достаточной точностью.

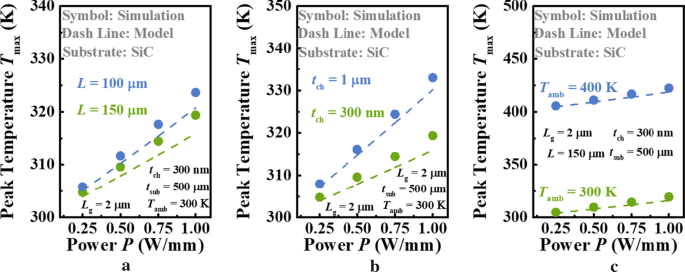
Зависимость T _макс Га ₂ О ₃ МОП-транзисторы с подложкой SiC на a длина устройства L , b толщина Ga ₂ О ₃ слой t _ch , и c температура окружающей среды T _amb на разной мощности P . Символы и линии обозначают результаты предложенной модели и моделирования соответственно

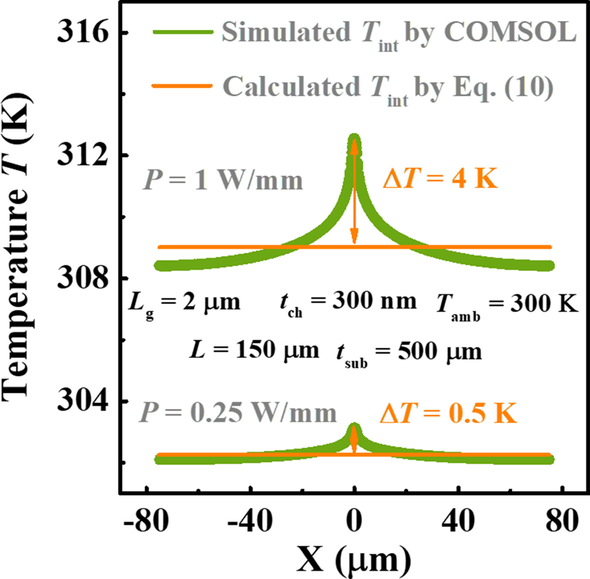
Сравнение T _int между смоделированными и рассчитанными по формуле. (10) при разных P

Выводы

Точная аналитическая модель для оценки T _макс Га ₂ О ₃ Представлены полевые МОП-транзисторы, в которых теплопроводность зависит от температуры и направления. Было получено простое выражение, основанное на геометрии устройства и параметрах материала. Было получено отличное согласие между моделью и численным моделированием COMSOL Multiphysics за счет варьирования различного энергопотребления. Предлагаемая модель для T _макс имеет большое значение для эффективного управления тепловым режимом силовых устройств, особенно Ga ₂ О ₃ МОП-транзисторы.

Доступность данных и материалов

Наборы данных, подтверждающие выводы этой статьи, включены в статью.

Сокращения

Ga ₂ О ₃ :

Оксид галлия

МОП-транзисторы:

Полевые транзисторы металл – оксид – полупроводник

AlGaN:

Нитрид алюминия-галлия

GaN:

Нитрид галлия

SiC:

Карбид кремния