Углы Эйлера робота:основной учебник для начинающих

Трудно разобраться с вращением робота, не так ли? Углы Эйлера - головная боль. Вот необходимое руководство, чтобы избавиться от боли.

Ориентация! Они просто заставляют меня хотеть рвать на себе волосы. Если вам когда-либо приходилось программировать конечную позу робота, используя координаты и повороты, вы поймете, о чем я говорю.

На первый взгляд установка положения исполнительного органа вашего робота кажется простой задачей, не так ли?

Вы просто говорите:"Я хочу переместить инструмент робота в это местоположение, и я хочу, чтобы оно указывало на это направление.”

Интуитивно вы точно знаете, какую ориентацию должен иметь инструмент. Однако когда дело доходит до описания ориентации с помощью точных чисел, эта простая задача внезапно превращается в беспорядок.

Почему трудно понять ориентацию роботов

Описать координаты X, Y, Z (поступательные) инструмента робота несложно.

Чтобы описать перевод, вы просто вводите координаты — например, Point[X, Y, Z] =[100, 1000, 1500] мм — и это может относиться только к одному местоположению, при условии, что вы используете одну и ту же базовую ссылку. Это может означать только 100 мм по оси X, 1 метр по оси Y и 1,5 метра по оси Z.

Но как вы описываете ориентацию инструмента?

Можно сказать:
Вращение[XYZ] =[5, 45, 15]°
однако можно также сказать (округляя числа)
Rot[XY'Z”] =[-7,9, 44,7, 16,2]°
или
Rot[ZY'Z”] =[7,9, 45,2, 5,0]°
или четный
кватернион[q1-q4] =[0,9, -0,1, 0,4, 0,1]

 Все они относятся к одной и той же ориентации!
Еще более непонятным является то, что разные производители роботов используют разные соглашения. Все это может стать головной болью, даже если вы знакомы с трехмерной геометрией.

Проблема:мы просто не думаем о ротациях

Настоящая проблема в том, что мы просто не думаем естественным образом в терминах поворотов.

Мы интуитивно понимаем переводческие координаты, потому что используем их в повседневной жизни (например, "Это на второй полке внизу, четыре книги слева". ). Однако, когда нам нужно описать ориентацию, мы прибегаем к тому, чтобы указать пальцем и сказать «Это в этом направлении».

К сожалению, роботам нужна более точная информация, чем расплывчатое "это там".

Нам нужно хорошее понимание углов Эйлера.

Что такое углы Эйлера?

Давайте сделаем шаг назад и начнем с основ.

Наиболее распространенным методом описания ориентации робота являются углы Эйлера. Углы Эйлера состоят из трех чисел, каждое из которых описывает вращение вокруг одной оси. Существуют различные соглашения об угле Эйлера в зависимости от порядка вращения.

Для начала упростим это до примера с одной осью.

Представьте компас.

Часто осью Z в мире называют ось, протянувшуюся от неба до земли. Таким образом, вы можете представить себе стрелку компаса как вращение вокруг оси Z (названное Rot[Z]). Когда вы держите компас горизонтально перед собой, а стрелка указывает на 135°, это означает, что север находится над вашим левым плечом, поэтому вы в настоящее время смотрите на юго-восток. Неважно, где вы расположите компас (на полу, на голове и т. д.), если он имеет одинаковую ориентацию, угол всегда будет равен 135°.

Пока все просто.

Наш компас имеет только одно значение поворота (например, Rot[Z]), но для описания любой трехмерной ориентации нам нужны три значения. Здесь все становится немного сложнее.

Другие методы описания ориентации робота — кватернионы или позы (матрицы 4 × 4).

Давайте возьмемся за дело

С этого момента вам будет полезно иметь интерактивное наглядное пособие.

Я предлагаю вам скачать бесплатную копию RoboDK по этой ссылке, которая позволяет очень легко визуализировать опорные системы и видеть полученные координаты.

Запустите RoboDK и создайте опорную рамку, используя кнопку «Добавить опорную рамку» или выбрав опцию в меню «Программа». Вы должны увидеть красную, зеленую и синюю рамку в центре экрана.

Вы можете повернуть рамку следующим образом:удерживайте нажатой клавишу Alt, затем щелкните и перетащите одну из появившихся изогнутых стрелок.

Как управлять самолетом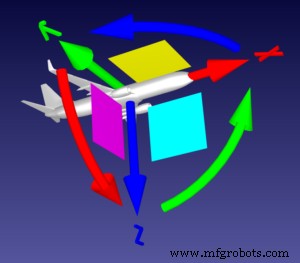

Давайте воспользуемся аналогией с самолетом, которая очень четко описана на форуме роботов.

Представьте, что опорная система — это плоскость. Наконечник прямой красной стрелки (ось X) – это кончик носового обтекателя, а прямая зеленая стрелка (ось Y) – его левое крыло.

В этом случае перемещение изогнутых стрелок выполняет следующие функции:

• Изогнутая красная стрелка =Rot[X]:Roll самолета, который позволяет плоскости вращаться вокруг своей горизонтальной оси.
• Изогнутая зеленая стрелка =Rot[Y]:шаг плоскости, указывающий носовым обтекателем вверх или вниз.
• Изогнутая синяя стрелка =Rot[Z]:рысканье самолета, определяющее направление движения самолета.

Если бы пилот хотел, чтобы самолет постепенно поворачивал влево и вниз, самолет не просто вращался бы вокруг оси Z — самолеты так не работают.

Вместо этого самолет:

1. Наклонить носовой обтекатель вниз:Rot[Y].
2. Повернуть самолет влево:-Rot[X]
3. Отклонение влево:Rot[Z]

Все это движение будет представлено как Rot[XYZ]. Попробуйте самостоятельно немного переместить рамку в RoboDK, пока не освоитесь с этими понятиями.

Затем дважды щелкните имя фрейма в левом верхнем углу главного окна, чтобы открыть панель «Сведения о фрейме».

Одна ориентация, несколько возможных поворотов

Используя RoboDK, попробуйте выполнить следующие задачи.

Перед каждой задачей сбрасывайте кадр, открыв значок меню "гамбургер" (три горизонтальные линии) на панели сведений о кадре и выбрав "Сбросить (установить идентификатор)".

1. Откройте раскрывающееся меню над координатами и выберите вращение Штойбли (X->Y’->Z") вместо общего.
2. Поверните рамку так, чтобы синий (Z) был направлен вниз, а красный (X) — назад (т. таким образом, вращая вокруг оси Y.
3. Сбросьте кадр, а затем снова переместите его на тот же угол поворота. Однако на этот раз используйте только один поворот по оси Z, а затем один поворот по оси X.
4. Сбросьте кадр, а затем снова переместите его на тот же угол поворота. Однако на этот раз используйте только один поворот по оси X, а затем один поворот по оси Z.

Как видите, одной и той же ориентации можно добиться несколькими способами.

Первый метод мы могли бы назвать Rot[Y], так как он включает только вращение вокруг оси Y. Второй метод мы могли бы назвать Rot[Z, X’], так как он включает в себя один поворот вокруг оси Z и один поворот вокруг новой оси X. Третий мы бы назвали Rot[X, Z’]. Штрих означает, что вращение происходит относительно последнего перемещения, а не относительно статических осей.

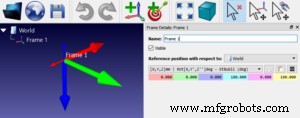
Это основная концепция углов Эйлера. Вы можете повернуть кадр в одну и ту же ориентацию несколькими способами, изменив последовательность осей и поворотов.

Разные производители роботов выбирают разные комбинации поворотов. Например, Stäubli использует условное обозначение XY’Z, Adept использует условное обозначение ZY’Z, KUKA использует условное обозначение ZY’X, а Fanuc &Motoman использует условное обозначение XYZ. С другой стороны, ABB использует Quaternion, а Universal Robots использует вектор ориентации. Но все соглашения можно использовать для представления любой ориентации в пространстве.

Дополнительную информацию можно найти в документации RoboDK.

Протестируйте различные соглашения о роботах

Надеюсь, это начинает проясняться. Однако это только начало. Чтобы по-настоящему освоить соглашения об углах Эйлера в RoboDK, я считаю полезным поиграть с программным обеспечением, следуя этому руководству.

Вы можете увидеть эффект поворота в цифрах в голубых, фиолетовых и желтых полях на панели «Сведения о кадре».

По умолчанию для новых систем отсчета выбирается общее соглашение XYZ. Попробуйте выбрать разных производителей роботов в раскрывающемся меню над цветными прямоугольниками. Попробуйте ввести числовые значения в поля, чтобы увидеть их влияние на систему отсчета.

Для подробного руководства по углам Эйлера я также могу порекомендовать эту страницу на Mecademic.