Эффективное прогнозирование и анализ оптического захвата в наномасштабе с помощью метода разрыва конечных элементов и соединения

Введение

Плазмонный оптический пинцет на основе поверхностных плазмонов (ПП) привлекает большое внимание и широко применяется для захвата наночастиц [1,2,3,4,5,6]. SP - это резонансное явление, вызванное взаимодействием падающего света с определенной длиной волны и свободных электронов на границе раздела металлов и диэлектриков [7]. SP позволяют оптическому пинцету преодолевать дифракционный предел. Более того, резкое усиление локального поля SP может снизить потребность в интенсивности падающего света [7, 8]. Однако SP тесно связаны с материалом и размерами объектов, а также с длиной волны падающего света, что требует большого количества экспериментов для определения оптимальных параметров оптических пинцетов SP на практике. Исходя из этого, метод моделирования играет все более важную роль в качестве вспомогательного средства для проектирования и оптимизации оптических пинцетов SP [9]. В этих симуляциях расчет оптической силы требуется для предсказания стабильного захвата. Для обычных объектов, таких как сферы, оптическую силу можно аналитически вывести из обобщенной теории Лоренца-Ми [10, 11]. Однако для объектов со сложной конфигурацией необходимы численные методы, которые строго решают основные уравнения Максвелла для моделирования электромагнитных полей и последующих оптических сил и потенциала.

Эти численные методы в основном можно разделить на методы дифференциальных уравнений (DEM) и методы интегральных уравнений (IEM) [12,13,14,15]. По сравнению с IEM методы дифференциальных уравнений (DEM) демонстрируют превосходные возможности при работе со сложной геометрией и компонентами. ЦМР также обладают преимуществом прямого вычисления распределения ближнего поля, которое играет важную роль в анализе SP. В качестве репрезентативной DEM метод конечных разностей во временной области (FDTD) реализуется во временной области, что позволяет легко получать широкополосную информацию и переходные характеристики [16, 17]. Однако FDTD требует точной дисперсионной модели для описания частотно-зависимых свойств материала в SP, в то время как точность решения FDTD сильно зависит от точности аппроксимации этой дисперсионной модели [18]. Кроме того, FDTD полагается на структурированные сетки, которые часто приводят к ошибкам лестницы для криволинейных поверхностей. В качестве еще одной типичной ЦМР широко применяется метод конечных элементов (МКЭ), поскольку он позволяет легко обрабатывать дисперсный материал в частотной области и устранять ступенчатую ошибку с помощью неструктурированной сетки [19,20,21,22]. По сравнению с FDTD, FEM может напрямую принимать измеренные параметры материала без какой-либо приближенной дисперсионной модели. Однако для резкого увеличения локального поля в SP требуется мелкая сетка дискретизации FEM. Кроме того, объекты с большими размерами и множественные объекты резко увеличивают количество неизвестных. Эти факторы вызовут плохую подготовку матричных систем и огромные вычислительные затраты, что создаст серьезные проблемы для традиционного МКЭ при анализе оптического захвата с улучшенным SP.

В этой статье представлен эффективный метод разрыва и соединения с двумя первичными конечными элементами (FETI-DP) для моделирования оптического захвата в наномасштабе. FETI-DP использует схему декомпозиции неперекрывающихся областей, которая разделяет исходную крупномасштабную сложную проблему на серию мелких простых задач для их решения. Он обеспечивает выполнение условия передачи на интерфейсах подобластей, чтобы гарантировать непрерывность поля, и вводит двойную переменную, чтобы уменьшить исходную трехмерную (3D) задачу до двумерной (2D) с помощью множителя Лагранжа. Первичные переменные в углах подобласти извлекаются, чтобы ускорить скорость сходимости итеративного решения двойственной задачи [23,24,25,26]. Для повышения производительности FETI-DP разработан подход низкоуровневого разбрызгивания. Он использует алгоритмы с разреженными данными для повышения эффективности решения проблем подобласти и двойственной задачи [27, 28]. Предлагаемый метод обеспечивает полностью разделенные подобласти, которые позволяют параллельно моделировать оптическую силу для захвата наночастиц. Тензор напряжений Максвелла (MST), который показывает взаимосвязь между электромагнитным полем и механическим импульсом, принят для оценки оптической силы [29]. На основе полученной оптической силы можно дополнительно рассчитать оптический потенциал для анализа устойчивого захвата. По сравнению с IEM, предлагаемый метод более эффективен при работе с составными материалами и решении ближнего поля для оптического захвата на основе SP. По сравнению с FDTD, предлагаемый метод позволяет точно обрабатывать дисперсный металлический материал в системах оптического улавливания на основе SP и устранять ступенчатую ошибку для объектов с криволинейной границей. По сравнению с МКЭ предлагаемый метод подходит для крупномасштабных вычислений оптического захвата. Проанализировано несколько примеров, и численные результаты демонстрируют точность и эффективность предлагаемого метода прогнозирования и анализа оптического захвата на наномасштабе.

Методы

Составы FETI-DP

Для реализации FETI-DP исходная вычислительная область Ω сначала разрывается на серию неперекрывающихся подобластей Ω ⁱ ( я =1, 2, 3 ⋯, N _s ), как показано на рис. 1. В каждой подобласти Ω ⁱ , подобластная система конечных элементов может быть получена из векторного волнового уравнения как

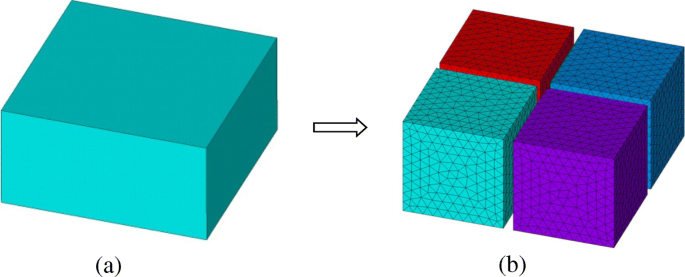
Схема разделения домена с неперекрывающимися подобластями в методе FETI-DP. а Оригинальный домен. б Разделенные субдомены и дискретные сетки

где E ^я обозначает неизвестное электрическое поле, которое необходимо решить в \ ({\ Omega} ^ i \), k ₀ и η ₀ - волновое число в свободном пространстве и собственный импеданс, соответственно, а \ ({\ mathbf {J}} _ i ^ {\ mathrm {imp}} \) - подаваемый ток. \ ({\ Gamma} _ {\ mathrm {ABC}} ^ i \) означает поглощающее граничное условие (ABC) для обрезания бесконечной открытой области. Следует отметить, что k ₀ должен быть заменен волновым сопротивлением в среде, если окружающая среда не является свободным пространством, что является обычным для оптического захвата. В интерфейсе субдомена Γ ⁱ , предполагаемое граничное условие требуется для генерации полной краевой задачи в Ω ⁱ . Здесь условие передачи типа Робина с неизвестной вспомогательной переменной Λ _я накладывается как

где \ ({\ hat {n}} ^ i \) обозначает единичный нормальный вектор, направленный наружу на интерфейсе подобласти Γ ⁱ , и α ^я - сложный параметр, который часто можно выбрать как jk ₀ . Затем все подобласти дискретизируются тетраэдрическими элементами. В каждом элементе мы раскрываем E с векторными базисными функциями N и неизвестный коэффициент электрического поля E как

где s обозначает количество векторных базисных функций в каждом элементе тетраэдра. s выбирается равным 6 для традиционной базисной функции нижнего порядка, основанной на ребре, в то время как оно больше для базовой функции вектора высокого порядка, поскольку вводятся дополнительные базисные функции, основанные на грани или объеме.

Применяя метод Галеркина, матричное уравнение МКЭ в Ω ⁱ о неизвестном коэффициенте электрического поля E ^я можно получить как

где нижний индекс c и r различать угловые степени свободы (DOF) и оставшиеся DOF, что извлекает угловые DOF как прямую переменную для построения схемы двойного первичного (DP). Здесь K - матрица системы МКЭ, а f - вектор возбуждения. Б - это логическая матрица, которая извлекает степени свободы интерфейса субдомена. λ - двойная переменная, созданная при раскрытии Λ _я , который также называют множителем Лагранжа.

Затем соседние подобласти могут быть соединены между собой путем обеспечения непрерывности тангенциального электрического поля и магнитного поля на границах раздела. Мы собираем все интерфейсы субдоменов и устраняем все внутренние неизвестные субдомены E ^я . Уменьшенное уравнение глобального интерфейса относительно двойной переменной λ можно получить как

Уравнение (6) может быть решено итерационными методами, такими как метод обобщенной минимальной невязки (GMRES). \ ({\ tilde {\ mathbf {K}}} _ {cc} \) - глобальная угловая система, которая может ускорить итеративную сходимость в прямом пространстве. Подходящий предварительный кондиционер может быть использован для повышения скорости итеративной сходимости, например, приблизительного обратного и неполного LU-разложения. Когда двойственная переменная λ решается, электрическое поле внутри каждой подобласти может быть независимо оценено с помощью (5). Для построения глобальной матрицы \ ({\ tilde {\ mathbf {K}}} _ {rr} \) необходимо построить числовую функцию Грина подобласти \ ({\ mathbf {Z}} _ {rr} ^ i \) с формой

куда включена обратная матрица FEM подобласти \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \). Кроме того, для матриц \ ({\ tilde {\ mathbf {K}}} _ {rc} \), \ ({\ tilde {\ mathbf {K}}} _ {cr} \) и \ ({\ tilde {\ mathbf {K}}} _ {cc} \) и векторы \ ({\ tilde {f}} _ r \) и \ ({\ tilde {f}} _ c \), \ ({\ left ({ \ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) требуется для вычисления. Конструкции \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) на этапе предварительной обработки, а также их матрично-векторные произведения (MVP) на этап итеративного решения требует больших вычислительных ресурсов. Хотя \ ({\ mathbf {K}} _ {rr} ^ i \) разреженный, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \ ) плотные, что означает большие вычислительные затраты. Затем вводится метод разрежения низкого ранга для ускорения вычисления \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \). Поскольку некоторые подматрицы в системе глобального интерфейса могут быть представлены в матричной форме низкого ранга, их вычисление может выполняться с помощью алгоритма низкого ранга, который улучшает производительность FETI-DP. Можно видеть, что FETI-DP обеспечивает независимые операции над субдоменами, поэтому он может использовать параллельные вычисления для повышения эффективности. Для эффективной параллельной схемы принцип разделения домена состоит в том, чтобы сделать количество степеней свободы в каждой подобласти как можно более сбалансированным. Следовательно, размер подобластей должен зависеть от плотности дискретизации сетки. Обычно небольшие подобласти принимаются в мелкоячеистых областях, в то время как большие подобласти принимаются в крупноячеистых областях.

Низкоуровневое разрежение

Предлагается низкоуровневый подход к разрежению, позволяющий использовать разреженные данные для повышения эффективности FETI-DP. Здесь data-sparse означает, что эти матрицы на самом деле не являются разреженными, но они разрежены в том смысле, что некоторые из них могут быть представлены в виде матриц разложения низкого ранга в виде

где X и Д находятся в полной матричной форме, а ранг k намного меньше м и н . Матрица \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) может быть представлена ​​матричными формами с разреженными данными, поскольку она обладает матричным свойством интеграла оператор. Следовательно, при условии, что \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) обладает свойством низкого ранга в данном субдомене, его можно эффективно вычислить и сохранить в формы с разреженными данными с использованием подхода низкоуровневого разрежения, который ускоряет MVP в итеративном решении.

Процессы низкорангового подхода к разрежению можно разделить на следующие этапы:(1) построить дерево кластеров, разбив базисную функцию, установленную в каждой подобласти, (2) построить дерево кластеров блоков путем взаимодействия двух деревьев кластеров, ( 3) сгенерировать разреженную данными форму \ ({\ mathbf {K}} _ {rr} ^ i \) по условию допустимости, (4) выполнить алгоритмы с низким рангом, чтобы получить разреженное данными представление \ ( {\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \), и (5) ввести решение систем FETI-DP с помощью алгоритм с разреженными данными. Для ускорения растворения можно использовать подходящий предварительный кондиционер. Следует отметить, что факторизация LU с разреженными данными \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS} } \) заменяет инверсию матрицы \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \). Техника вложенного рассечения используется для дальнейшего повышения эффективности разреженного анализа низкого ранга. Вложенное рассечение использует разделители для получения больших недиагональных нулевых субблоков, которые будут сохранять ноль во время факторизации LU, что может значительно уменьшить количество заполнений.

Чтобы сгенерировать \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), мы сначала строим дерево кластеров T _Я рекурсивным разделением набора базисных функций на основе ребер подобласти I ={1,2, …… N } используя ограничивающую рамку. При вложенном разрезе кластер t в соответствующей ограничительной рамке делится на три последователя { s ₁ , s _sep , s ₂ }, где s ₁ и s ₂ являются индексными наборами двух отсоединенных ограничивающих рамок и s _sep - это индексный набор разделителя. На рис. 2а показан простой пример этого процесса. Затем дерево кластеров блоков T _{Я × Я} можно построить путем взаимодействия двух кластерных деревьев T _Я , как показано на рис. 2b, которое может быть выбрано в качестве кластерного дерева исходного набора краевых базисных функций и набора тестовых базисных функций в методе Галеркина. Затем нам нужно ввести условие допустимости, основанное на вложенном разрезе, чтобы различать полные блоки, блоки разложения низкого ранга и недиагональные нулевые блоки в T _{Я × Я} [23]. Таким образом, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) может быть получен путем заполнения соответствующих блоков ненулевыми элементами \ ({\ mathbf {K}} _ {rr} ^ i \). Наконец, LU-факторизация с разреженными данными \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L }} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \ ) можно вычислить рекурсивно из

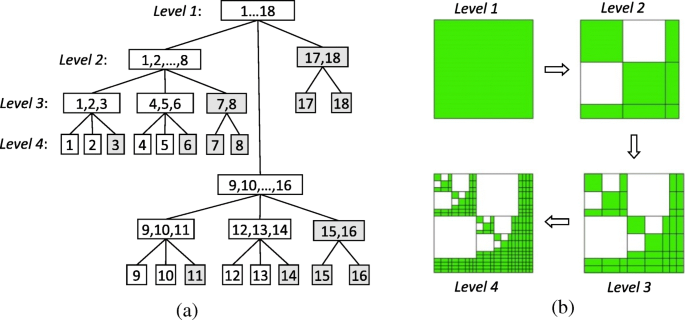
Построение дерева кластеров и дерева кластеров из 4 уровней на основе вложенного анализа. а Построение дерева кластеров путем рекурсивного разделения набора базисных функций на основе ребер I ={1,2,… 18}. б Построение дерева кластеров блоков, где белый блоки - нулевые матрицы и зеленые блоки могут быть полными матрицами или матрицами разложения низкого ранга

где традиционная полная матричная арифметика заменена их аналогами с разреженными данными [28]. Ошибка адаптивного усечения ε _т используется для контроля точности приближений низкого ранга. Полученные коэффициенты LU \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) и \ ({\ left ({\ mathbf {U}) } _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) сохраняются и используются для построения \ ({\ mathbf {Z}} _ {rr} ^ i \) с помощью

где \ ({\ mathbf {B}} _ r ^ i {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \) и \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} {\ mathbf {B}} _ r ^ i \) может быть вычисляется решателем верхнего и нижнего треугольников с разреженными данными. \ ({\ Left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), \ ({\ left ({\ mathbf {U}} _ { rr} ^ i \ right)} _ {\ mathrm {DS}} \) и \ ({\ mathbf {Z}} _ {rr} ^ i \) входят в расчет FETI-DP с разреженными данными вперед и назад замены (FBS) и MVP с разреженными данными.

Оптическая сила и потенциал

Согласно теории электродинамики, оптическую силу можно оценить с помощью тензора напряжений Максвелла (MST), который показывает связь между электромагнитным полем и механическим импульсом [29]. После получения распределения электромагнитного поля вокруг объекта оптическую силу можно рассчитать путем интегрирования MST по замкнутой поверхности, окружающей объект. На основе полученного распределения электрического поля можно построить МСТ в любых координатах

где верхний индекс звездочка обозначает сопряженное электрическое поле или магнитное поле, ε равны μ - диэлектрическая проницаемость и магнитная проницаемость, а \ (\ overleftrightarrow {\ mathbf {I}} \) - единичная матрица 3 × 3. По внешнему произведению векторов тензорную форму \ (\ overleftrightarrow {\ mathbf {T}} \) можно записать как

где нижний индекс x , y , z обозначает компоненты в трех направлениях. Согласно расширению E описанные в (4), записи MST T _мин ( м , n = x , y , z ) могут быть преобразованы в развернутые формы при расчете FETI-DP как

где ω - угловая частота; N и s были описаны в формуле. (4).

Наконец, оптическая сила, действующая на объект, может быть рассчитана путем интегрирования MST по любой замкнутой поверхности, окружающей его

Обратите внимание, что расчет оптической силы также может быть реализован параллельно, поскольку интеграл MST присваивается соответствующим подобластям. Для стабильного оптического захвата одним из основных условий является то, что градиентная сила должна быть больше силы рассеяния. Другими словами, направление общей силы должно быть идентично направлению градиентной силы, которая всегда указывает на положение, в котором напряженность электрического поля наиболее велика.

Оптический потенциал - еще один привлекательный параметр, показывающий стабильность оптического захвата. На основании полученной оптической силы глубина оптического потенциала U в позиции r ₀ можно рассчитать по

где нижний индекс ∞ обозначает бесконечность, определяемую как контрольную точку с нулевым потенциалом. Значение U может быть представлен как k _B T, где k _B обозначает постоянную Больцмана 1,3806488 × 10 ⁻²³ Дж / К и Т - температура окружающей среды. Как правило, частица может преодолевать броуновское движение в растворе и стабильно удерживаться в ловушке, когда U > 1 k _B Т. доволен. В противном случае частица не может быть устойчиво захвачена. Поскольку полная оптическая сила включает в себя консервативный градиентный компонент силы и неконсервативный компонент силы рассеяния, полная оптическая сила F из (15) неконсервативно [30, 31]. Однако при условии, что движение наночастицы ограничено одним измерением, это дает однозначное определение оптического потенциала из (16), даже несмотря на то, что полная оптическая сила неконсервативна.

Результаты и обсуждение

Приведены три примера, демонстрирующих эффективность предложенного метода. Поскольку для возбуждения поверхностного плазмона обычно используются благородные металлы, мы выбираем репрезентативные материалы из золота и серебра для анализа. В первом примере рассчитывается оптическая сила наночастицы серебра для проверки точности предлагаемого метода. Второй и третий примеры моделируют и обсуждают оптический захват наночастиц золота. Для всех примеров бесконечная область усекается с помощью ABC, а расстояния между ABC и объектами устанавливаются равными одной длине волны, что достаточно для достижения приемлемой точности. Все расчеты выполняются на рабочей станции Dell, оснащенной процессорами Intel Xeon с тактовой частотой 3,6 ГГц.

Серебряная нанокапсула

Сначала рассматривается объект серебряной нанокапсулы для проверки точности и эффективности предложенного метода FETI-DP в прогнозировании оптической силы. На рис. 3 а и б представлены его конфигурация и размеры. Основными параметрами серебра являются все измеренные значения, взятые из [32]. Для реализации схемы FETI-DP вся область анализа сначала делится на 24 поддомена. Более плотные сетки необходимы вблизи поверхности металла для моделирования эффекта усиления локального плазмонного поля. Для дискретизации приняты тетраэдрические элементы, что дает всего 6,9 × 10 ⁵ неизвестные, в том числе 4,1 × 10 ⁴ двойные неизвестные и 313 угловых неизвестных. Падающий свет светится в направлении + z , а направление поляризации электрического поля - x .

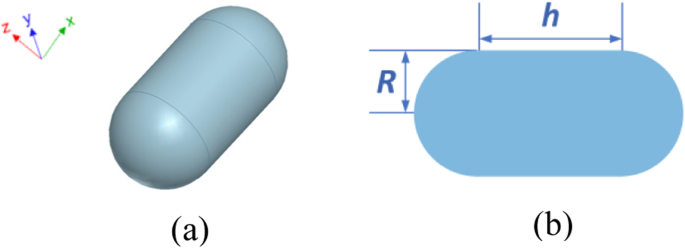
Конфигурация структуры серебряной нанокапсулы. а 3D вид. б Вид спереди и размеры, где R =30 нм и h =60 нм

Сначала мы меняем длину волны падающего света λ от 200 до 400 нм для имитации оптических сил, действующих на нанокапсулу. Поскольку FETI-DP работает в частотной области, оптические силы рассчитываются в 15 точках частоты дискретизации. На рис. 4 показана расчетная кривая оптических сил, действующих на серебряную нанокапсулу. Чтобы указать точность FETI-DP, результаты оптической силы FETI-DP сравниваются с результатами коммерческого программного обеспечения Lumerical FDTD Solutions [33], и можно наблюдать хорошее совпадение.

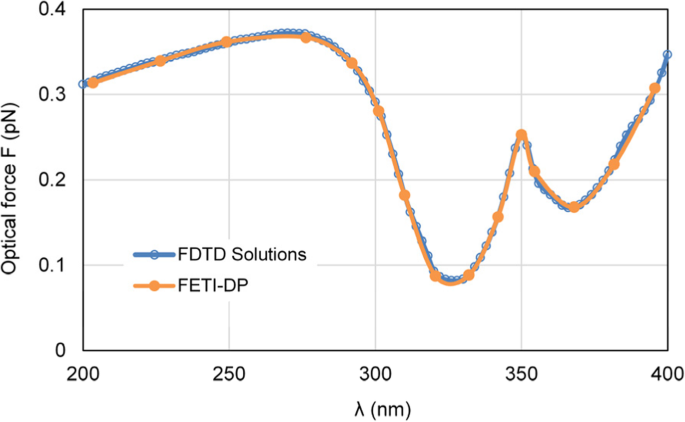
Результаты воздействия оптических сил на серебряную нанокапсулу, изменяющихся в зависимости от длины волны λ падающего света, включая результаты FETI-DP и коммерческих программных решений FDTD

Затем производительность FETI-DP тестируется для разного количества поддоменов. Увеличиваем количество подобластей с 4 до 24, сохраняя плотность дискретизации. Мы назначаем каждому процессору работу с одним поддоменом. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF  = ‖OF _я  − OF _ref ‖/‖OF _ref ‖, where OF _я is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is a plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10 ⁶ unknowns, including 1.6 × 10 ⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. а 3D view. б Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by

where \( {T}_{N_p} \) denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ  = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

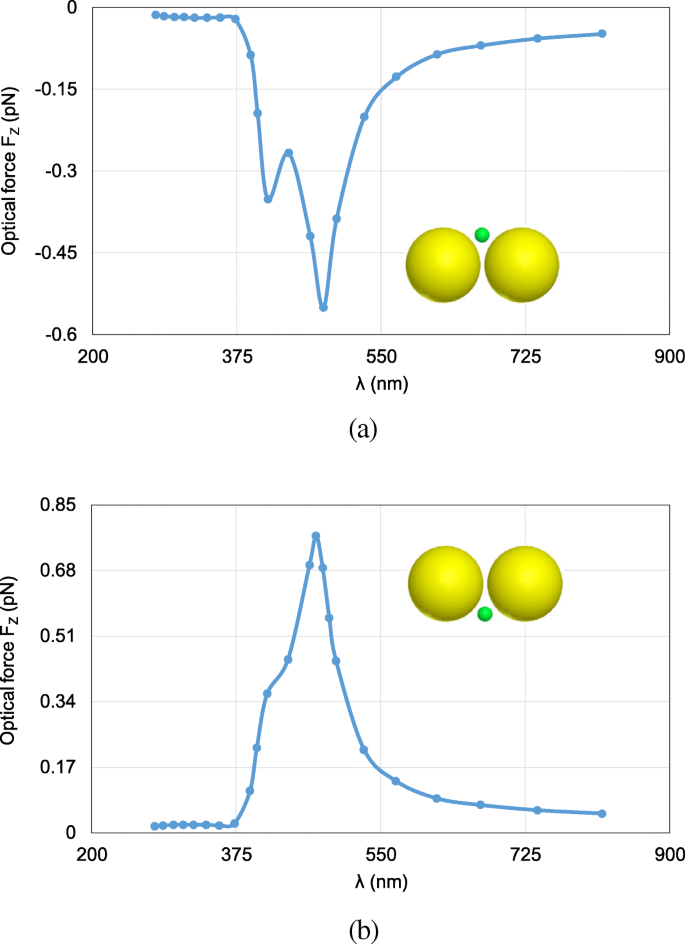
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. а The object nanosphere is located at (0, 0, 20 nm). б The object nanosphere is located at (0, 0, − 20 nm)

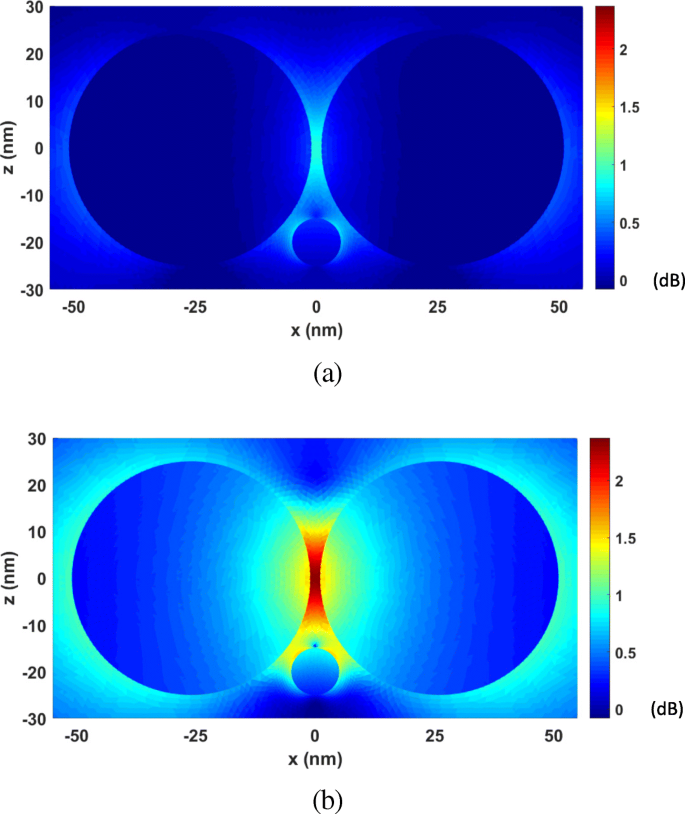
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. а λ = 300 nm (non-resonance wavelength). б λ  = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -ось. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -ось. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

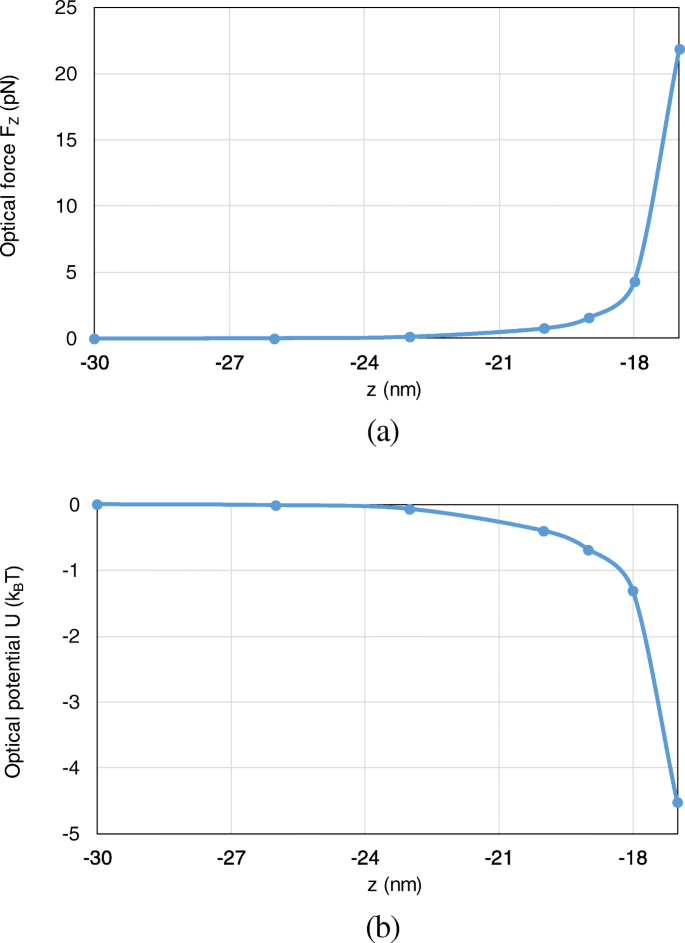
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). а The optical forces. б The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10 ⁻² , which is defined as |F ₁  − F ₀ |/|F ₀ |.

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r  = 2.25. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10 ⁶ unknowns, including 1.3 × 10 ⁵ dual unknowns and 1227 corner unknowns.

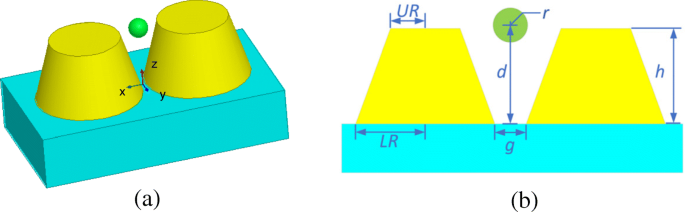
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. а 3D view. б Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ  = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

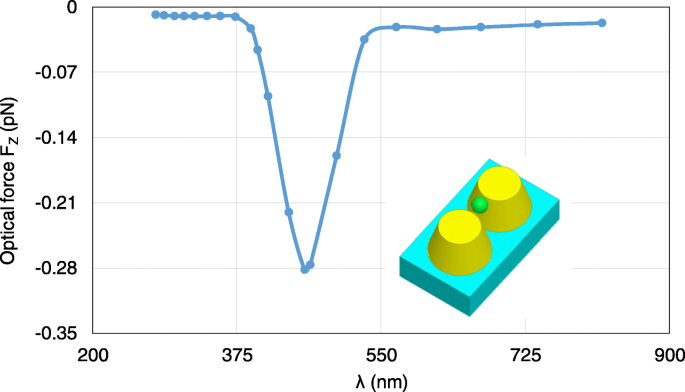
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

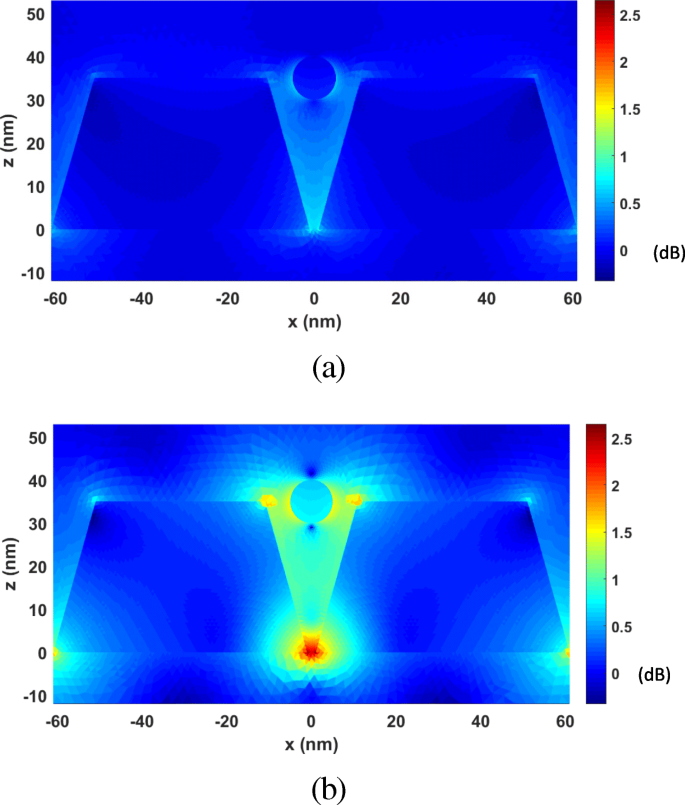
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. а λ =300 nm (non-resonance wavelength). б λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

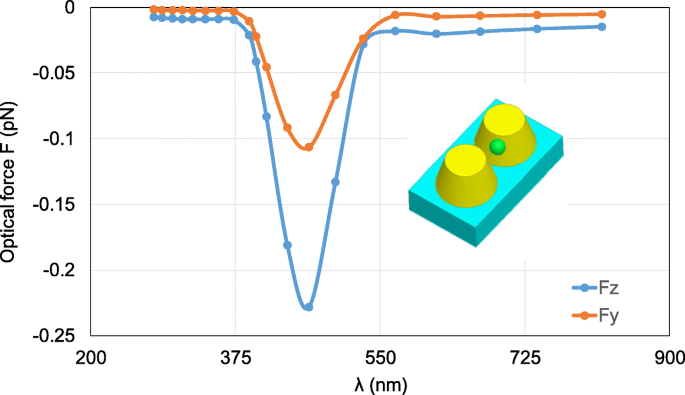
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -ось. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

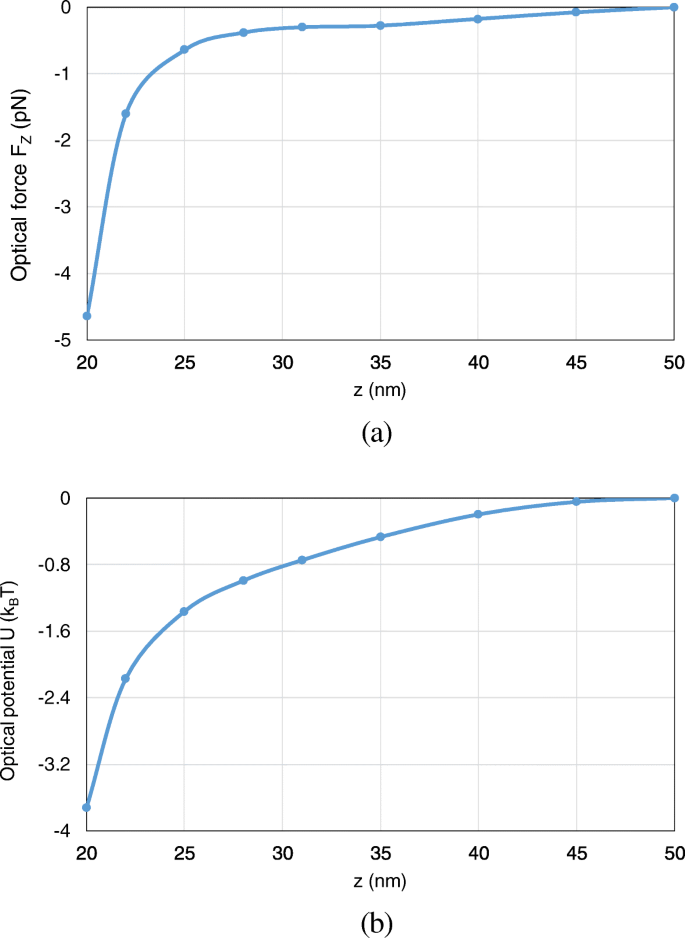
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). а The optical forces. б The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Заключение

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Доступность данных и материалов

All data generated or analyzed during this study are included in this article.

Сокращения

ABC:

Absorbing boundary condition

DOF:

Degrees of freedom

FDTD:

Конечная разность во временной области

FEM:

Метод конечных элементов

FETI-DP:

Dual-primal finite element tearing and interconnecting

MST:

Maxwell stress tensor

MVP:

Matrix-vector product