Малоугловое рассеяние от наноразмерных жирных фракталов

Введение

Многие иерархические структуры, генерируемые в нано- и микромасштабе, обладают геометрическими характеристиками, которые инвариантны относительно масштабных расширений, демонстрируют самоподобие и, таким образом, обладают фрактальными свойствами [1, 2]. Хотя недавние достижения в области материаловедения и нанотехнологий позволяют получать различные искусственные нано- / микромасштабные детерминированные фракталы с точным самоподобием [3–7], подавляющее большинство природных процессов порождают случайные, статистически самоподобные фракталы. Хорошее приближение в структурных исследованиях природных фрактальных образований можно сделать, прибегая к детерминированным фрактальным моделям с той же фрактальной размерностью, что и у случайных. Этот подход был успешно использован, чтобы показать, что перенос через случайные фрактальные поверхности очень близок к отклику детерминированной геометрии модели [8]. Путем введения полидисперсности в алгоритм построения детерминированного фрактала можно получить такие же интенсивности малоуглового рассеяния (SAS), что и соответствующие случайным фракталам [9]. Кроме того, «детерминированный» подход является более эффективным в вычислительном отношении, позволяя аналитически описывать различные свойства, такие как фрактальная форма, структурные факторы и радиус вращения.

Одним из наиболее надежных методов определения структурных свойств как детерминированных, так и случайных фракталов [10, 11] является использование дифракции волн в контексте малоуглового рассеяния на нано- или микроструктурированных материалах с использованием нейтронов или электромагнитных волн (x -луча, света и др.) [12]. Вот почему одной из фундаментальных задач теоретических описаний, связанных с экспериментальными определениями в этой области исследований, является выявление взаимосвязи между структурой фракталов и их соответствующим дифракционным спектром или распределением интенсивности рассеяния в зависимости от волнового вектора рассеяния. В этом направлении выполнено множество экспериментальных и теоретических исследований [13–21].

Используя стандартные теоретические вычисления и интерполяцию, параметром, который определяется на основе таких экспериментальных измерений, является массовая фрактальная размерность D _м (см. Приложение 1), с D _м D _s , с d -1 < D _s < г . Мы обозначили d евклидово измерение, в которое встроен фрактал. Фрактальная размерность массы описывает способ, которым масса M ( г ) меняется, когда он встраивается в диск радиуса r . Полученное масса-радиус отношение \ (M (r) \ propto r ^ {D _ {\ mathrm {m}}} \) приводит к поведению интенсивности рассеяния \ (I (q) \ propto q ^ {- D _ {\ mathrm {m} }} \). Очевидно, D _м можно отождествить с показателем степенной зависимости интенсивности рассеяния как функции от волнового вектора рассеяния q [18, 22]. Чем выше значение D _м , тем компактнее конструкция. Точно так же в случае поверхностного фрактала его поверхностное распределение подчиняется \ (S (r) \ propto r ^ {2-D _ {\ mathrm {s}}} \), и, следовательно, \ (\ phantom {\ dot { i} \!} I (q) \ propto q ^ {- (2 \ mathrm {d} -D _ {\ mathrm {s}})} \) [19, 23]. Работая в трехмерном евклидовом пространстве, D _s приближается минимум к двум, когда поверхность почти идеально гладкая. Максимум три, если он сложен так, что почти полностью заполняет пространство.

Многие экспериментальные интенсивности дифракции от различных химически синтезированных и биологических систем характеризуются в двойном логарифмическом масштабе последовательностью степенных затуханий, перемежающихся областями постоянной интенсивности. Такое поведение может быть идентифицировано для некоторых полимерных гелей [24], гликозидгидролазы для целлобиозного субстрата [25], комплексных полиэлектролитных коацерватов [26] или нанопористого углерода [27]. Хотя классическая модель Бокажа [28] может предоставить основную структурную информацию об этих системах (т. Е. Массовую или фрактальную размерность поверхности и общий размер каждого структурного уровня), требуется более полная характеристика из-за большого количества конфигураций, которые соответствуют фиксированное значение фрактальной размерности. Этот вопрос недавно был частично рассмотрен Черным и соавт. [29] в контексте моделей малоуглового рассеяния (SAS). Было показано, что для детерминированных массовых фракталов с единым масштабом может быть получена дополнительная информация, такая как номер итерации фрактала, количество основных составляющих единиц и коэффициент масштабирования. Этот подход, кроме того, успешно использовался для разработки новых моделей толстых фракталов, если в распределениях рассеяния присутствуют последовательности степенных затуханий. Его можно применять к конструкциям, у которых общий размер основных составляющих элементов такого же порядка, как и расстояния между ними [30, 31].

Теоретическая модель, представленная в этой статье, объединяет предыдущие модели, чтобы расширить их применимость. Он описывает последовательность степенных распадов с произвольно уменьшающимися значениями показателей рассеяния, и перемежается областями постоянной интенсивности. Наша модель также может предоставить более подробную информацию о каждом структурном уровне в нано- / микрофрактале. Для этой цели мы рассматриваем толстый фрактал, представленный двумерным детерминированным массовым фракталом с коэффициентом масштабирования, который зависит от числа итераций, но с ненулевой площадью поверхности в пределе большого количества итераций, поэтому с положительным Мера Лебега. Мы выводим аналитические выражения фрактальной формы и структурных факторов, а также показываем, как определять фрактальные размеры и коэффициенты масштабирования на каждом структурном уровне.

Теоретические основы

Учитывая набор одинаково ориентированных идентичных дифракционных апертур, обозначенных здесь Σ , содержащий N прозрачные области, помеченные j необходимо учитывать суммирование по амплитудам, полученным от каждой апертуры. Итак, известное частотное распределение дифракционной амплитуды одиночной апертуры (уравнение (37) в Приложении 2) можно переписать как [32]:

Координаты точки в локальном кадре j апертура ( x _j , y _j ) и T ( x, y ) представляет собой индивидуальную функцию передачи, соответствующую каждой прозрачной области. Можно заменить суммирование на интегрирование, потому что в нашем случае отверстия описываются одной и той же индивидуальной функцией распределения, так что уравнение (1) можно переписать как:

Интегральный коэффициент из предыдущего равенства представляет собой преобразование Фурье функции распределения каждой из идентичных апертур, как указано выше. Эта амплитуда модулируется множителем, содержащим суммирование, представляющее преобразование Фурье дельта-распределений Дирака в форме \ (A _ {\ delta} ~ =~ \ sum _ {j ~ =~ 1} ^ {N} (x ~ - ~ x_ {j}) (y ~ - ~ y_ {j}) \). Следовательно, также учитывается пространственное распределение апертур внутри решетки. Таким образом, уравнение. (2) можно переписать в форме, известной как теорема о массивах [32]:

Распределение интенсивности дифрагированного изображения в плоскости Фурье принимает следующий вид:

Как и следовало ожидать, первый множитель в произведении соответствует интенсивности рассеяния отдельного отверстия, а второй показывает, как эти отверстия распределены в дифракционной апертуре Σ . Эти величины также известны как форм-фактор F . ( p, q ) и, соответственно, структурный фактор S ( p, q ). Вот почему результаты, полученные на протяжении всего документа, будут выражены с использованием следующей формы интенсивности рассеяния:

Модель и метод жирных фракталов

Подробная процедура построения тонкого (регулярного) канторовского фрактала хорошо известна [33]. Здесь резюмируется только основная процедура строительства. Применяется подход сверху вниз. Начиная с начального квадрата (или любой другой евклидовой формы) с ребром l ₀ (на м =0), центр которого совпадает с началом декартовой системы координат, а ребра параллельны осям системы координат, любая точка квадрата удовлетворяет условиям - l ₀ / 2≤ х ≤ l ₀ / 2 и - l ₀ / 2≤ y ≤ l ₀ / 2. На первой итерации ( m =1), квадрат делится на четыре других квадрата с длиной ребра \ (\ beta _ {\ mathrm {s}} ^ {(1)} l_ {0} \). Мы обозначили \ (\ beta _ {\ mathrm {s}} ^ {(1)} \ Equiv (1- \ gamma _ {1}) / 2 \), \ (0 <\ beta _ {\ mathrm { s}} ^ {(1)} <1/2 \), коэффициент масштабирования первой итерации, и с γ ₁ доля удаленной длины в этой точке, как видно на рис. 1 a, b) для m =1. Число, помещенное между (⋯), появляющееся как верхний индекс, количественно определяет номер итерации. Его нельзя интерпретировать как показатель степенной функции. С точки зрения коэффициента масштабирования положения четырех квадратов задаются векторами \ (\ boldsymbol {a} _ {j} ~ =~ \ left \ {\ pm \ beta _ {\ mathrm {t}} ^ { (1)} l_ {0}, \ pm \ beta _ {\ mathrm {t}} ^ {(1)} l_ {0} \ right \} \) со всеми возможными комбинациями знаков, где \ (\ beta _ { \ mathrm {t}} ^ {(1)} ~ =~ \ left (1- \ beta _ {\ mathrm {s}} ^ {(1)} \ right) / 2 \) используется для дальнейшего упрощения формулировок. В качестве исходной формы выбран квадрат из-за простоты численных расчетов. Можно рассматривать любую другую геометрическую форму, например круг. Эффект от выбора другой формы наблюдается только в области Porod форм-фактора, что выходит за рамки данной статьи.

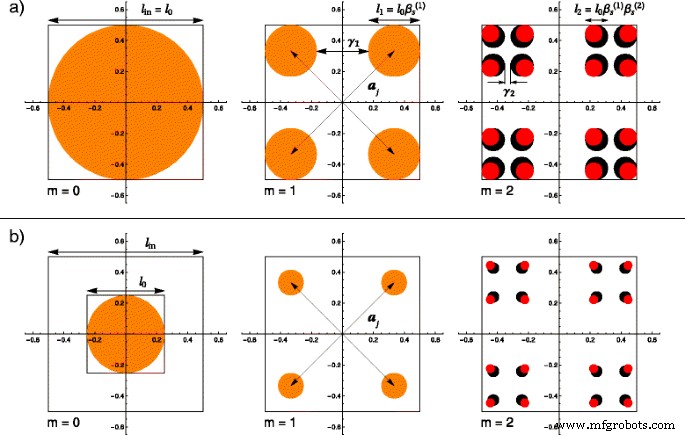
(Цветной онлайн) Сравнение обычных и толстых фракталов для первых двух итераций, где базовая форма на уровне m =0 - диск диаметром l ₀ и размер фрактала l _в : а l ₀ = l _в ; б l ₀ = l _в / f , с f =2. В обоих случаях на м =1 структуры совпадают из-за одинаковых коэффициентов масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(1)} \). Начиная с м =2, толстый фрактал имеет больший коэффициент масштабирования \ (\ left (\ beta _ {\ mathrm {s}} ^ {(2)}> \ beta _ {\ mathrm {s}} ^ {(1)} \ справа) \), и поэтому диски имеют больший диаметр ( черные диски ), чем в случае обычного фрактала ( красные диски ); а _j - векторы положения и γ _я - доли удаленной длины в i й итерация

Первые два описанных выше шага также применяются при построении классической версии толстого фрактала для итераций m =0 и м =1. Поэтому до сих пор эти две структуры совпадают. Для получения жирного фрактала была использована модификация алгоритма на итерации m =1, выбрав другой коэффициент масштабирования m =2, \ (\ beta _ {\ mathrm {s}} ^ {(2)} \ Equiv (1 - \ gamma _ {2}) / 2 \). Применяя весь алгоритм в пределе большого количества итераций [34, 35], мы повторно получаем классическую версию толстого фрактала. Из построения ясно, что обычная версия фрактала восстанавливается, когда коэффициенты масштабирования на каждой итерации выбираются равными \ (\ beta _ {\ mathrm {s}} ^ {(1)} ~ =~ \ beta _ {\ mathrm {s}} ^ {(2)} ~ =~ \ cdots =\ beta _ {\ mathrm {s}} ^ {(m)} \).

Чтобы получить постоянное плато между двумя степенными затуханиями в поведении интенсивности ПАВ, мы должны принять во внимание, что расстояния между рассеивающими единицами намного больше, чем их общий размер. Такой подход впервые был использован в контексте поверхностных фрактальных моделей [36, 37]. Учитывая соотношение f от общего расстояния между рассеивающими элементами l _в и их общий размер l ₀ , в одном есть:

Для экспериментов по рассеянию, отображающих плато постоянной интенсивности между двумя фрактальными областями, значения f Следует выбрать ≫1. В случае поверхностных фракталов увеличение значения f приводит к лучшему согласованию между полной интенсивностью ПАВ, с одной стороны, и приближением независимых единиц рассеяния, с другой [36, 37].

Используя приведенные выше соображения, можно описать различия между обычными и жирными фракталами. Влияние фактора f , представленное выше, также можно визуализировать. Вот почему на рис. 1 мы графически проиллюстрируем сравнение с использованием диска радиуса r ₀ ≡ l ₀ / 2 = l _в / (2 f ) в качестве нашей основной формы. Результаты первых двух итераций, отображаемые в каждой строке рис.1, представляют структуры, полученные для обычного фрактала (отмеченного красными дисками) и толстого фрактала (представленного в виде черного диска), которые также могут быть полностью перекрыты ( помечены оранжевыми дисками). В строке, обозначенной на рис. 1 a, коэффициент f считается равным единице, так что получаются классические конструкции и фрактальные формы. Вторая строка рисунка, обозначенная на рис. 1, б, демонстрирует влияние указанного выше фактора. В этих вычислениях мы выбрали произвольное значение f =2. Видно, что на итерациях m =0 и м =1, как в случае a, так и в случае b полученные структуры регулярного и толстого канторовских множеств идентичны и полностью перекрываются. Этого следовало ожидать из-за общего коэффициента масштабирования. Однако, как видно на последней паре изображений на рис. 1, начиная с m =2, радиусы дисков толстого фрактала больше, потому что его коэффициент масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) по определению больше, чем у обычного. На последнем изображении с рис. 2b размер дисков намного меньше, чем на его аналоге с рис. 2а из-за неунитарного значения множителя f .

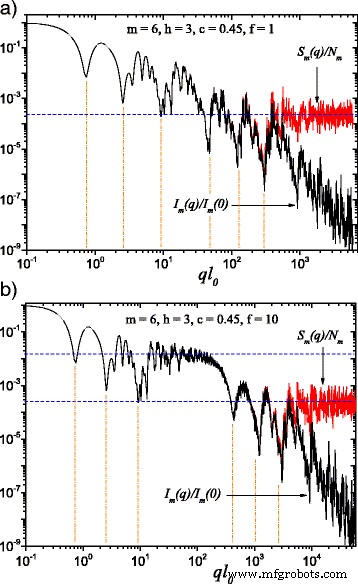
(Цветной онлайн) Сравнение интенсивности рассеяния по формуле. (22) ( черные кривые ) и структурный фактор, задаваемый формулой. (24) ( красные кривые ) на м =6 и усреднено по ориентациям согласно формуле. (25). Здесь h =3 (т.е. коэффициент масштабирования остается постоянным для трех последовательных итераций), в то время как основная форма при вычислении интенсивности рассеяния - это квадрат с размером края l ₀ : а l ₀ = l _в ; б l ₀ = l _в / f (с f =10). Когда f 1, между двумя обобщенными степенными затуханиями появляется плато постоянной интенсивности (рис. 2, б). Горизонтальные линии обозначим асимптоту структурного фактора ≃1 / N _м , а положения минимумов оцениваются по формуле. (26)

Для получения самих степенных законов необходимо дальнейшее обобщение классической модели толстых фракталов. Это делается с учетом того, что изменение коэффициента масштабирования происходит не на каждой итерации, а каждую секунду, третью, ⋯ или, вообще говоря, каждые h -я итерация. Доля удаленных длин на м итерация:

с 0 < c <1. Функция p _м определяется как:

для любого положительного целого значения m , с h =1, ⋯, м , где использовалась минимальная функция ⌊ ⋯ ⌋. Таким образом, коэффициент масштабирования, соответствующий m итерация задается следующим образом:

Теперь ясно, что цель функции p _м - сохранить коэффициент масштабирования постоянным для h итерации ( h < м ).

Компоненты векторов положения каждого квадрата можно записать как:

а длина края каждого квадрата определяется как:

Фактор f используется в формуле длины l ₀ принять во внимание, что для итераций между ( h +1) й и м -го, размер квадратов уменьшается пропорционально расстоянию между ними:

где h < м . Количество квадратов на каждой итерации:

Таким образом, в каждом масштабе, рассматриваемом как итерация с постоянным коэффициентом масштабирования, имеется различная фрактальная размерность, заданная формулами [29, 38, 39]:

В пределе большого количества итераций фрактальная размерность построенного фрактального множества будет [34]:

что является ожидаемым значением для двумерного толстого фрактала. Наконец, если a _я относительная площадь, удаленная в i й итерации, то \ (\ prod _ {i =1} ^ {m} (1-a_ {i})> 0 \), если \ (\ sum _ {i =1} ^ {\ infty} a_ {i} <\ infty \), и, таким образом, модель удовлетворяет определению и характеристикам толстых фракталов [35].

Результаты и обсуждение

По принципу Бабине можно сделать вывод, что на м На итерации решетки отверстия в решетке представляют собой оставшиеся квадраты фрактала, а удаленные части становятся непрозрачными для излучения.

Интенсивность монодисперсного рассеяния и структурный фактор

Чтобы получить аналитическое выражение интенсивности рассеяния для толстого фрактала Кантора, мы начнем с записи рекуррентного соотношения пропускания решетки для произвольной итерации, соответствующей 1 D кейс. На м =0, имеем

С учетом алгоритма построения фрактала коэффициент пропускания после первой итерации определяется как:

$$ \ begin {align} T_ {1} (l_ {1}, x,) =T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x-l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right) + \\ T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x + l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right), ~~~~~~~~~~~~ \ end {выровнено} $$ (17)

где δ ( x - а ) - одномерное дельта-распределение Дирака в x = а . Символ * обозначает оператор свертки. Следовательно, на м -ю итерацию можно написать:

$$ \ begin {align} T_ {m} (l_ {m}, x) =T_ {m-1} (l_ {m}, x) \ ast \ delta \ left (\ frac {x-u_ {m} } {l_ {m}} \ right) + \\ T_ {m-1} (l_ {m}, x, y) \ ast \ delta \ left (\ frac {x + u_ {m}} {l_ {m }} \ right), ~~~~~~~~~~~~ \ end {align} $$ (18)

где \ (u_ {m} ~ =~ l_ {0} \ beta _ {\ mathrm {t}} ^ {(m)} \ prod _ {j =1} ^ {m-1} \ beta _ {\ mathrm {s}} ^ {(j)} \). Выполнение преобразования Фурье по уравнению. (18), получается, что амплитуда рассеяния на m итерация:

$$ A_ {m} (p) =2 ^ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ prod \ limits_ {i =1} ^ { m} \ cos (2 \ pi p u_ {i}). $$ (19)

Поскольку 2 D Модель толстого фрактала является прямым продуктом двух одномерных толстых фракталов, ее преобразование Фурье может быть записано как произведение двух одномерных преобразований Фурье. Следовательно, двумерная амплитуда рассеяния может быть записана как:

$$ A_ {m} (p, s) \ Equiv A_ {m} (p) A_ {m} (s), $$ (20)

и, таким образом,

$$ \ begin {align} A_ {m} (p, s) =N_ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ {m})} {\ pi s l_ {m}} \ times \\ \ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}), \ end {align} $$ (21)

так что интенсивность рассеяния становится:

$$ \ begin {align} I_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin ( \ pi s l_ {m})} {\ pi s l_ {m}} \ right) ^ {2} \ times \\ N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ right) ^ {2}. \ конец {выровнено} $$ (22)

Первый множитель в предыдущем уравнении, представляющий интенсивность дифракции из-за форм-фактора, как указано в уравнении. (5):

$$ F_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ { m})} {\ pi s l_ {m}} \ right) ^ {2}, $$ (23)

соответствует интенсивности рассеяния, полученной от одного квадрата со стороной l _м . Второй фактор, представляющий интенсивность дифракции из-за структурного фактора, как указано в формуле. (5):

$$ S_ {m} (p, s) =N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ right) ^ {2}, $$ (24)

описывает способ распределения квадратов. Полная интенсивность рассеянного излучения - произведение F _м ( p, s ) и S _м ( p, s ).

Степенное затухание интенсивности, как сформулировано в формуле. (22), получается после усреднения по всем ориентациям [29]. Учитывая равную вероятность для любой ориентации, среднее значение может быть вычислено в случае двумерных фракталов путем интегрирования по всем направлениям вектора рассеяния q =( p, s ):

$$ \ langle f (p, s) \ rangle =\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} f (q, \ phi) \ mathrm {d} \ phi, $ $ (25)

где p = q cos ϕ и s = q грех ϕ . Таким образом, интенсивность рассеяния I ( д ) получается как функция модуля переданного импульса q ≡ | q |.

Потому что из определения структурного фактора \ (S_ {m} (0) ~ =~ N_ {m} ^ {2} \), где N _м количество квадратов, как определено в формуле. (13) стандартная процедура нормализации S _м (0) =1 можно принять, как описано в [11, 29].

Результаты, рассчитанные для интенсивности монодисперсного рассеяния I _м ( д ) и структурный фактор S _м ( д ), с м =6, показаны на рис. 2 для классического жирного фрактала ( f =1 на рис. 2 а), а для расширенной модели фракталов жира, разработанной в данной работе ( f =10 на рис.2, б). Чтобы получить рис. 2b, мы рассмотрели h =3, чтобы коэффициент масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) первых трех итераций оставался постоянным, затем он имел другое постоянное значение \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) для следующих трех итераций. Как и ожидалось, в обоих случаях (для f =1 и f =10), различия между интенсивностью рассеяния, с одной стороны, и структурным фактором, с другой, можно наблюдать, когда \ (q \ gtrsim 1 / l_ {m} \). В этой области интенсивность рассеяния имеет степенной спад I ( д ) ∝ q ⁻³ . Структурный фактор имеет асимптотическое значение, стремящееся к 1 / N . _м , представленный горизонтальной линией на Рис. 2a или нижней горизонтальной линией на Рис. 2b [29, 33].

Последовательность двух обобщенных степенных распадов, идентифицируемых как суперпозиция максимумов и минимумов, по сравнению с простым степенным распадом, можно увидеть на рис. 2а. Но на рис. 2b область примерно постоянной интенсивности в области 20≲ ql ₀ 100, можно четко различить, охваченный двумя последовательными обобщенными степенными затуханиями. Это связано с уменьшением размеров квадратов на порядок ( f =10) по сравнению с расстояниями между ними. Эта область, наблюдаемая вокруг верхней горизонтальной линии на рис. 2b, имеет асимптоту 1 / N ₃ , то же самое, что и фактор структуры классического толстого фрактала, демонстрируя поведение, аналогичное случаю рассмотрения только первых трех итераций.

Кроме того, на рис. 2 можно увидеть, что количество минимумов в каждом масштабе совпадает с количеством итераций с постоянным коэффициентом масштабирования. Эти минимумы возникают, когда излучение, проходящее через разные квадраты внутри фрактала, интерферирует и находится в противофазе, и, следовательно, наиболее часто встречающиеся расстояния между центрами квадратов (2 u _м ) равны π / q . Поэтому приблизительное положение минимумов получается из соотношения:

$$ q_ {i} \ simeq \ frac {\ pi} {2 u_ {i}}, ~~~~ i =1, \ cdots, m $$ (26)

обозначены на рис. 2 вертикальными линиями. Для первых шести итераций наблюдается довольно хорошее согласие между положениями, вычисленными по формуле. (26), и найденные в интенсивности рассеяния или структурном факторе. Это приближение может быть менее точным для более высоких итераций, если номер итерации превышает определенное значение, потому что в этих случаях все больше и больше расстояний сопоставимы с наиболее часто встречающимся. Тем не менее, это приближение должно хорошо работать на практике, где вряд ли можно ожидать различить более четырех или пяти таких минимумов.

Для каждой отдельной шкалы в заданном диапазоне 1 / (2 u _я ) ≲ q ≲1 / (2 u _{я +1} ) дифракционная картина создается интерференцией только i -я фрактальная итерация. Это можно использовать, чтобы показать, что в пределах этого интервала функции I _м ( д ) q ^Д и S _м ( д ) q ^Д логопериодичны [29], где D - фрактальная размерность, соответствующая заданному масштабу. В частности, для результатов, представленных на рис. 2 и 3 функции I _м ( д ) q ^-1,1 и S _м ( д ) q ^-1,1 логопериодичны с периодом \ (1 / \ beta _ {\ mathrm {s}} ^ {(1)} \) для первых трех итераций, а I _м ( д ) q ^-1,51 и S _м ( д ) q ^-1,51 логопериодичны с \ (1 / \ beta _ {\ mathrm {s}} ^ {(2)} \) для второй группы из трех итераций.

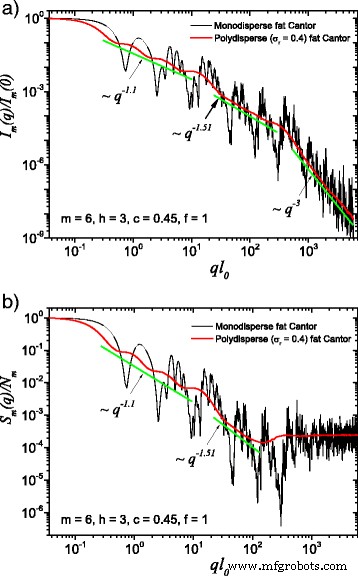
(Цветной онлайн) Сравнение монодисперсной и полидисперсной систем: a интенсивность рассеяния (уравнение (22)); б структурный фактор (уравнение (24)), усредненный по всем ориентациям фрактала, согласно уравнению. (25). Здесь f =1, м =6, h =3 (т.е. коэффициент масштабирования остается постоянным в течение трех последовательных итераций), а основная форма представляет собой квадрат с начальной длиной ребра l ₀ = l _в . В обоих случаях полидисперсность размывает кривые монодисперсного рассеяния, и фрактальные размерности могут быть восстановлены на каждом структурном уровне

Подобно детерминированным массовым фракталам, уравнение. (26) можно использовать для получения нескольких структурных параметров, характеризующих фракталы жира. Во-первых, общее количество минимумов совпадает с общим количеством фрактальных итераций. На рисунке 2 показано, что фрактал состоит из трех итераций с коэффициентом масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) и трех итераций с коэффициентом масштабирования \ (\ beta _ {\ mathrm {s} } ^ {(2)} \). Во-вторых, из периодичности этих минимумов (или из периодичности I _м ( д ) q ^Д и S _м ( д ) q ^Д ), коэффициенты масштабирования можно восстановить. На рис. 2b коэффициент масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) может быть получен из периодичности минимумов в ql ₀ ≃7,25 и 90, а коэффициент масштабирования \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) можно получить из периодичности минимумов в ql ₀ ≃400, 1000 и 2500. Кроме того, длина промежуточного плато между фрактальными областями может использоваться как показатель отношения ( f ) расстояний между рассеивающими элементами и их габаритными размерами. На рис. 2b этот диапазон соответствует 13≲ ql ₀ ≲130.

Интенсивность полидисперсного рассеяния и структурный фактор

В этой части нашей работы мы можем теперь учесть, что размеры решетки подчиняются функции распределения D _N ( l ₀ ), определенный таким образом, что D _N ( l ₀ ) d l ₀ дает вероятность того, что размер фрактальной решетки находится в интервале ( l ₀ , l ₀ + d l ₀ ). Этот шаг вводит полидисперсность в нашу модель фракталов жира. Мы проиллюстрируем это, выбрав логнормальное распределение:

$$ D _ {\ mathrm {N}} (l_ {0}) =\ frac {1} {\ sigma l_ {0} (2 \ pi) ^ {1/2}} e ^ {- \ frac {\ left (\ log (l_ {0} / \ mu) + \ sigma ^ {2} / 2 \ right) ^ {2}} {2 \ sigma ^ {2}}}, $$ (27)

с относительной дисперсией \ (\ sigma _ {\ mathrm {r}} =\ left (\ left \ langle l_ {0} ^ {2} \ right \ rangle _ {D} - \ mu ^ {2} \ right) ^ {1/2} / \ mu \), среднее значение μ =〈 l ₀ 〉 _D , and variance \(\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}\). Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:

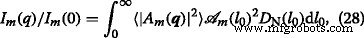
где is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term 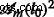[29].

The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ _r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ _r , the positions of main minima and maxima are still observable.

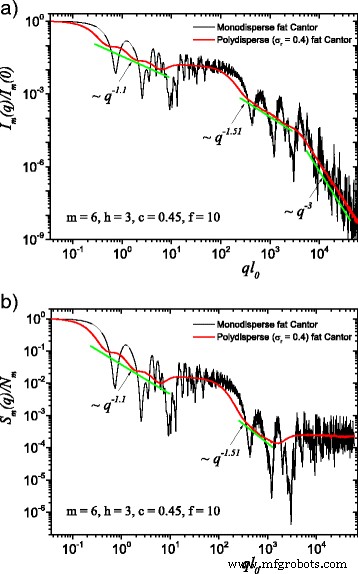
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); б structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql ₀ ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l ₀ =l _in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level

More generally, for small values of σ _r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ _r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.

Conclusions

In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.

Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.

We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.

The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.

Appendix

fractal dimension

Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D _м ).

In general terms, the mass-radius relation can be rewritten as [2]:

where the scaling law correction A (r ) tends to a constant value if r →∞ .

If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l ₀ , composed of k elementary units at the first iteration, each of size β _s l ₀ , where β _s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:

one can write M (l ₀ )=kM (β _s l ₀ ). Используя уравнение. (29), one obtains a direct method to compute the fractal dimension, via:

fraunhofer diffraction and the array theorem

Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z направление. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:

In the previous formula, \(r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}\) is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .

Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:

This approximation leads to the Fresnel diffraction integral:

where the prefactor P (u,v ) is given by

и k =2π /λ . Considering, in addition, that the condition z ≫k Max(x ² +y ² )/2 is satisfied, one has \(\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1\). Rewriting Eq. (34), the Fraunhofer approximation becomes:

Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space: