Преобразование из десятичной нумерации

Поскольку восьмеричная и шестнадцатеричная системы счисления имеют основание, кратное двоичному (основание 2), преобразование между шестнадцатеричным, восьмеричным и двоичным числами очень просто.

Кроме того, поскольку мы хорошо знакомы с десятичной системой, преобразовать двоичную, восьмеричную или шестнадцатеричную в десятичную форму относительно легко (просто сложите произведения зашифрованных значений и весовых коэффициентов).

Однако преобразование десятичной дроби в любую из этих «странных» систем счисления - другое дело.

Метод проб и испытаний

Метод, который, вероятно, будет иметь наибольший смысл, - это метод «проб и подгонки», когда вы пытаетесь «подогнать» двоичное, восьмеричное или шестнадцатеричное представление к желаемому значению, представленному в десятичной форме.

Например, предположим, что я хотел представить десятичное значение 87 в двоичной форме. Начнем с рисования поля двоичного числа со значениями весовых коэффициентов:

Что ж, мы знаем, что у нас не будет бита «1» вместо 128, потому что это сразу даст нам значение больше 87.

Однако, поскольку следующий вес справа (64) меньше 87, мы знаем, что у нас там должна быть «1».

Если бы мы сделали следующее место справа также «1», наше общее значение было бы 64 ₁₀ + 32 ₁₀ , или 96 ₁₀ . Это больше 87 ₁₀ , поэтому мы знаем, что этот бит должен быть «0».

Если мы сделаем следующий (16-й) разрядный бит равным «1», это приведет к нашему общему значению 64 ₁₀ + 16 ₁₀ , или 80 ₁₀ , что ближе к нашему желаемому значению (87 ₁₀ ), не превышая его:

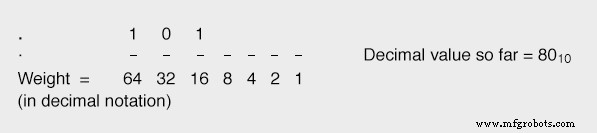
Продолжая эту последовательность действий, устанавливая каждый бит меньшего веса, поскольку нам нужно приблизиться к желаемому общему значению, не превышая его, мы в конечном итоге придем к правильному значению:

Метод проб и подгонки в восьмеричном и шестнадцатеричном формате

Эта пробная стратегия также будет работать с восьмеричными и шестнадцатеричными преобразованиями. Возьмем ту же десятичную цифру 87 ₁₀ , и преобразовать его в восьмеричную систему счисления:

Если мы поставим цифру «1» на место 64, у нас будет общее значение 64 ₁₀ . (менее 87 ₁₀ ). Если мы поставим цифру «2» на место 64, у нас будет общее значение 128 ₁₀ . (больше 87 ₁₀ ). Это говорит нам о том, что наша восьмеричная система счисления должна начинаться с «1» вместо 64:

Теперь нам нужно поэкспериментировать со значениями шифра в месте 8, чтобы попытаться получить общее (десятичное) значение как можно ближе к 87, не превышая его. Пробуя первые несколько вариантов шифрования, получаем:

Шифрование «3» на месте 8 приведет нас к желаемому результату в 87 ₁₀ . , так что цифра 2!

Конечно, если в последнем разделе вы обращали внимание на восьмеричные / двоичные преобразования, вы поймете, что мы можем взять двоичное представление (десятичное) 87 ₁₀ , который мы ранее определили как 1010111 ₂ , и легко преобразовать его в восьмеричное, чтобы проверить нашу работу:

Можем ли мы таким же образом выполнить преобразование десятичного числа в шестнадцатеричное? Конечно, но кому захочется? Этот метод прост для понимания, но трудоемок в исполнении.

Есть еще один способ сделать эти преобразования, который, по сути, тот же (математически), но его легче выполнить.

Техника повторного деления

В этом другом методе используются повторяющиеся циклы деления (с использованием десятичной записи), чтобы разбить десятичную систему счисления на кратные двоичные, восьмеричные или шестнадцатеричные значения разряда.

В первом цикле деления мы берем исходное десятичное число и делим его на основание системы счисления, в которую мы конвертируем (двоичная =2 восьмеричная =8, шестнадцатеричная =16).

Затем мы берем целочисленную часть результата деления (частное) и снова делим ее на базовое значение, и так далее, пока не получим частное меньше 1.

Двоичные, восьмеричные или шестнадцатеричные цифры определяются «остатками», оставшимися после каждого шага деления. Давайте посмотрим, как это работает для двоичного кода, на примере десятичного числа 87 ₁₀ :

Двоичные биты собираются из остатков последовательных шагов деления, начиная с LSB и переходя к MSB. В этом случае мы приходим к двоичной записи 1010111 ₂ .

Когда мы делим на 2, мы всегда будем получать частное, оканчивающееся на «.0» или «.5», то есть остаток от 0 или 1. Как было сказано ранее, этот метод повторного деления для преобразования будет работать для нумерации системы кроме двоичных.

Если бы мы выполняли последовательные деления с использованием другого числа, например 8 для преобразования в восьмеричное, мы обязательно получим остатки от 0 до 7. Давайте попробуем это с тем же десятичным числом, 87 ₁₀ :

Мы можем использовать аналогичный метод для преобразования систем счисления, работающих с величинами меньше 1.

Для преобразования десятичного числа меньше 1 в двоичное, восьмеричное или шестнадцатеричное мы используем многократное умножение, принимая целую часть произведения на каждом шаге в качестве следующей цифры преобразованного числа.

Давайте использовать десятичное число 0,8125 ₁₀ в качестве примера преобразование в двоичный:

Как и в случае с повторным делением для целых чисел, каждый шаг дает нам следующую цифру (или бит) дальше от «точки».

При целочисленном (делении) мы работали от младшего разряда к старшему (справа налево), но при повторном умножении мы работали слева направо.

Чтобы преобразовать десятичное число больше 1 с компонентом <1, мы должны использовать оба техники, по одному. Возьмем десятичный пример 54,40625 ₁₀ , преобразование в двоичный:

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист систем счисления