Сравнение десятичного и двоичного чисел

Давайте посчитаем от нуля до двадцати с использованием четырех различных систем счисления:хеш-меток, римских цифр, десятичных и двоичных чисел:

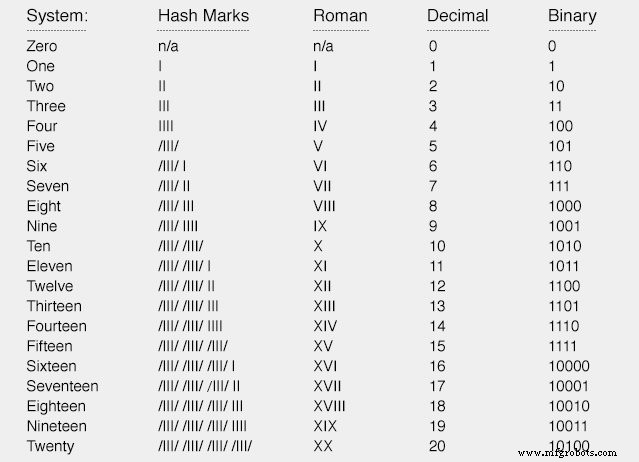
Ни решетки, ни римская система не подходят для обозначения больших чисел. Очевидно, что для этой задачи более эффективны системы с взвешиванием по месту, такие как десятичная и двоичная.

Однако обратите внимание, насколько более короткая десятичная запись превосходит двоичную при том же количестве величин. То, что занимает пять битов в двоичной системе счисления, занимает всего две цифры в десятичной системе счисления.

Это поднимает интересный вопрос относительно различных систем счисления:насколько большое число может быть представлено ограниченным числом позиций или мест шифра? При использовании грубой системы хеш-меток количество разрядов ЯВЛЯЕТСЯ наибольшим числом, которое может быть представлено, поскольку для каждого целочисленного шага требуется одна хеш-метка «место».

Однако для систем счисления со взвешенными позициями ответ можно найти, взяв основу системы счисления (10 для десятичной, 2 для двоичной) и возведя ее в степень числа знаков.

Например, 5 цифр в десятичной системе счисления могут представлять 100 000 различных целочисленных значений от 0 до 99 999 (10 в 5-й степени =100 000). 8 битов в двоичной системе счисления могут представлять 256 различных целочисленных значений от 0 до 11111111 (двоичное) или от 0 до 255 (десятичное), поскольку 2 в восьмой степени равны 256.

С каждой дополнительной позицией в числовом поле возможность представления чисел увеличивается в разы по основанию (10 для десятичного числа, 2 для двоичного).

Интересная сноска по этой теме - один из первых электронных цифровых компьютеров Eniac.

Разработчики Eniac решили представлять числа в десятичной форме, в цифровом виде, используя серию схем, называемых «кольцевыми счетчиками», вместо того, чтобы просто использовать двоичную систему счисления, чтобы минимизировать количество схем, необходимых для представления и вычислений. большие числа.

Такой подход оказался контрпродуктивным, и с тех пор практически все цифровые компьютеры были исключительно двоичными по конструкции.

Преобразование двоичного числа в десятичное

Чтобы преобразовать число в двоичной системе счисления в его эквивалент в десятичной форме, все, что вам нужно сделать, это вычислить сумму всех произведений битов с соответствующими константами весовых коэффициентов. Для иллюстрации:

Крайний правый бит называется младшим значащим битом (LSB), потому что он занимает место с наименьшим весом (место единицы).

Бит в дальнем левом углу называется наиболее значимым битом (MSB), потому что он занимает место наивысшего веса (место сто двадцать восемь).

Помните, что битовое значение «1» означает, что соответствующий вес разряда добавляется к общему значению, а битовое значение «0» означает, что соответствующий вес разряда не добавляются к общей стоимости. В приведенном выше примере мы имеем:

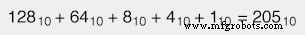
Если мы встречаем двоичное число с точкой (.), Называемое «двоичной точкой», а не десятичной точкой, мы следуем той же процедуре, понимая, что вес каждого места справа от точки составляет половину значения один слева от него (так же, как каждое место имеет вес справа от десятичной дроби точка составляет одну десятую веса того, что находится слева от нее). Например:

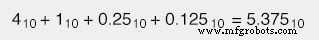
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист двоичной математики