19 Модуль 2:Программируемые оси станков с ЧПУ и системы измерения положения
ЦЕЛЬ
После завершения этого раздела вы сможете:
- Знакомство с декартовой системой координат.
- Понимать декартовы координаты плоскости.
- Знакомство с декартовыми координатами трехмерного пространства.
- Понимание четырех квадрантов.
- Объясните разницу между полярной и прямоугольной координатами.
- Определите программируемые оси на станке с ЧПУ.
ДЕРКОВА СИСТЕМА КООРДИНАТ
Декартовы координаты позволяют задать положение точки на плоскости или в трехмерном пространстве. Декартовы координаты или прямоугольная система координат точки представляют собой пару чисел (в двух измерениях) или тройку чисел (в трех измерениях), которые задают расстояния со знаком от оси координат. Сначала мы должны понять систему координат, чтобы определить наши направления и относительное положение. Система, используемая для определения точек в пространстве путем установления направления (оси) и опорного положения (начала). Система координат может быть прямоугольной или полярной.
Точно так же, как точки на прямой могут быть поставлены в однозначное соответствие с линией действительных чисел, так и точки на плоскости могут быть помещены в соответствие один к одному с парами строк действительных чисел с помощью двух координатных линий. Для этого построим две перпендикулярные координатные линии, пересекающиеся в своих началах; для удобства. Назначьте набор равновеликих делений для осей x и y, начиная с начала координат и идущих в обоих направлениях, влево и вправо (ось x) и вверх и вниз (ось y) точки вдоль каждой оси. Мы делаем одну из числовых линий вертикальной с положительным направлением вверх и отрицательным направлением вниз. Другие числовые линии горизонтальны с положительным направлением вправо и отрицательным направлением влево. Две числовые линии называются осями координат; горизонтальная линия — это ось x, вертикальная линия — это ось y, а оси координат вместе образуют декартову систему координат или прямоугольную систему координат. Точка пересечения осей координат обозначается буквой О и является началом системы координат. См. рис. 1.
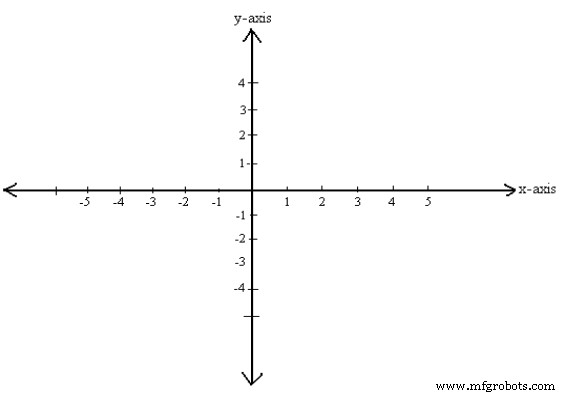
Рис. 1
По сути, это две линии с действительными числами, соединенные вместе:одна идет влево-вправо, а другая вверх-вниз. Горизонтальная линия называется осью X, а вертикальная линия называется осью Y.
Происхождение
Точке (0,0) дается специальное имя «Начало», а иногда и буква «О».
Строка действительных чисел
Основой этой системы является числовая линия, размеченная через равные промежутки. Ось помечена (X, Y или Z). Одна точка на линии обозначается как начало координат. Числа на одной стороне линии отмечены как положительные, а числа на другой стороне отмечены как отрицательные. См. рис. 2.
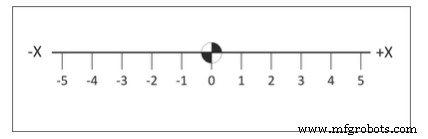
Рисунок 2. Числовая линия по оси X
Декартовы координаты плоскости
Плоскость, в которой введена прямоугольная система координат, является плоскостью координат или плоскостью x-y. Теперь мы покажем, как установить однозначное соответствие между точками на координатной плоскости и парами действительных чисел. Если А — точка на координатной плоскости, то через А мы проводим две прямые, одну перпендикулярную оси х, а другую — перпендикулярную оси у. Если первая линия пересекает ось x в точке с координатой x, а вторая линия пересекает ось y в точке с координатой y, то мы связываем пару (x, y) с A (см. рисунок 2). Число a является координатой x или абсциссой P, а число b является координатой y или ординатой p; мы говорим, что A является точкой с координатой (x, y) и обозначаем точку через A (x, y). Точке (0,0) дается специальное имя «Начало», а иногда и буква «О».
Абсцисса и ордината:
Слова «Абсцисса» и «Ордината»… это просто xandyvalues:
- Абсцисса:горизонтальное значение ("x") в паре координат:насколько далеко расположена точка.
- Ордината:значение по вертикали ("y") в паре координат:насколько далеко вверх или вниз находится точка.
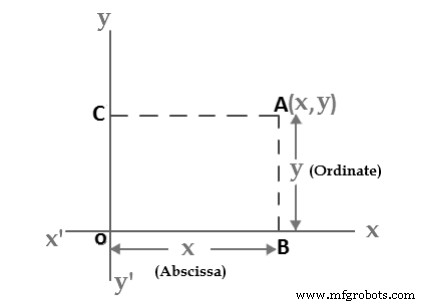
Рис. 3
Отрицательные значения X и Y:
Строка действительных чисел также может иметь отрицательные значения.
Отрицательный:начать с нуля и двигаться в противоположном направлении; См. рис. 4
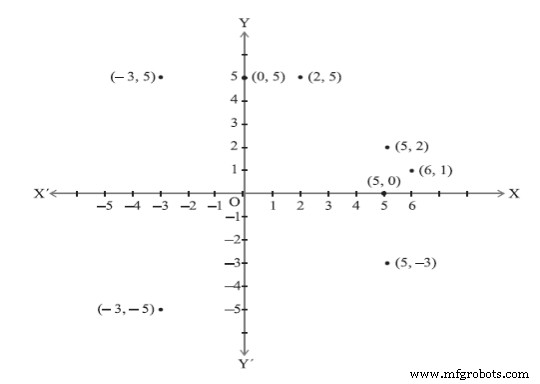
Рис. 4
Итак, для отрицательного числа:
- goleftfor x
- спуститься
влево по оси x 3, затем вверх на 5 по оси y. (Квадрант II x отрицательный, y положительный) И (-3,-5) означает:
влево по оси x 3, затем вниз 5 по оси y. (Квадрант III x отрицательный, y отрицательный) Используя декартовы координаты, отметьте точку на графике, как далеко вдоль и как высоко она находится; См. рисунок 5. Точка (12,5) находится на расстоянии 12 единиц по оси x и на 5 единиц вверх по оси y.
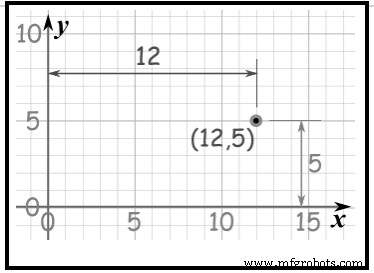 Рис. 5Оси X и Y:
Рис. 5Оси X и Y:  Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе строки проходят через ноль(Origin, (0,0)).
Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе строки проходят через ноль(Origin, (0,0)).  Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе линии проходят через ноль(Origin, (0,0)). Соедините их на графике… См. рис. 6
Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе линии проходят через ноль(Origin, (0,0)). Соедините их на графике… См. рис. 6 
Рис. 6
По сути, это набор из двух строк с действительными числами.
Ось:опорная линия, от которой измеряются расстояния.
Пример:
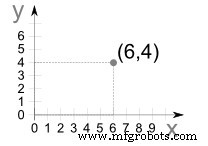 Точка(6,4) равна
Точка(6,4) равна Пройдите по оси X 6 единиц, затем поднимитесь на 4 единицы вверх в их направлении, затем «поставьте точку».
И вы можете запомнить, какая ось какая:
Координаты всегда записываются в определенном порядке:
- сначала расстояние по горизонтали,
- затем расстояние по вертикали.
Заказная пара:
Числа разделяются запятой, а все это заключено в круглые скобки следующим образом: (7,4)
Пример:(7,4) означает 7 единиц вправо (ось X) и 4 единицы вверх (ось Y)
Декартовы координаты трехмерного пространства
В трехмерном пространстве (пространстве xyz), ориентированном под прямым углом к плоскости xy. Ось z проходит через начало координат плоскости xy. Координаты определяются по направлениям восток-запад по оси x, север-юг по оси y и смещения вверх-вниз по оси z от начала координат. Декартова система координат основана на трех взаимно перпендикулярных координатных осях:ось х, ось они и ось z, см. рис. 6 ниже. Три оси пересекаются в точке, называемой началом координат. Вы можете представить себе начало координат в точке, где стены в углу комнаты встречаются с полом. Ось x — это горизонтальная линия, вдоль которой пересекаются стена слева от пола. Их-ось — это горизонтальная линия, по которой пересекаются стена справа от вас и пол. Ось z — это вертикальная линия, по которой пересекаются стены. Части линий, которые вы видите, стоя в комнате, являются положительной частью каждой из осей. Отрицательная часть этих осей будет продолжением линий за пределами комнаты.
Рис. 7. Трехмерная декартова система координат
Трехмерные декартовы оси координат. Представление трех осей трехмерной декартовой системы координат. Положительная ось x, положительная ось y и положительная ось z — это стороны, обозначенные x, y и z. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (сторона без метки) является отрицательной частью.
При работе с трехмерным движением необходимо настроить подходящую систему координат. Наиболее простой тип системы координат называется декартовой системой. Декартова система координат состоит из трех взаимно перпендикулярных осей, осей X, Y и Z. По соглашению ориентация этих осей такова, что, когда указательный, средний и большой пальцы правой руки расположены взаимно перпендикулярно, указательный, средний и большой пальцы могут быть взаимно перпендикулярны. выровнены по осям X, Y и Z соответственно. Такая система координат называется правой. См. рис. 7. Точка пересечения трех осей координат называется началом системы координат.
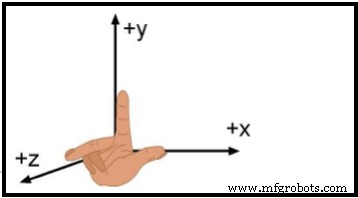
Рис. 8. Правосторонняя декартова система
Декартовы координаты точки в трех измерениях представляют собой тройку чисел (x, y, z). Три числа или координаты определяют расстояние со знаком от начала координат по осям x, y и z соответственно. Их можно визуализировать, сформировав прямоугольник с ребрами, параллельными оси координат и противоположными углами в начале координат и заданной точке.
Точки теперь могут быть определены в трехмерном объеме пространства. Это позволяет определять точки в трех измерениях от начала координат. Декартовы координаты (x, y, z) точки в трех измерениях определяют расстояние со знаком от начала координат по осям x, y и z соответственно. Точки оси Z становятся третьей записью при определении местоположений координат.
Учитывая приведенную выше аналогию с углом комнаты, мы могли бы сформировать декартовы координаты точки на макушке следующим образом. Представьте, что ваш рост составляет пять метров по оси Z, и вы проходите два метра от начала координат по оси X, затем поворачиваете налево и идете параллельно оси Z на четыре метра в комнату. Декартовы координаты точки на макушке будут (2,4,5).
Например, обозначение (2,4,5) соответствует значению X2, Y4 и Z5. См. рис. 8.
3 параметра
Декартовы координаты можно использовать для определения местоположения точек в трех измерениях, как в этом примере:

Рисунок 9. Точка (2, 4, 5 ) показан в трехмерных декартовых координатах.
Квадранты
Оси координат делят плоскость на четыре части, называемые квадрантами (см. рис. 9). Квадранты пронумерованы против часовой стрелки, начиная с верхнего правого угла, обозначены I, II, III и IV с обозначениями осей, как показано на рисунке ниже.
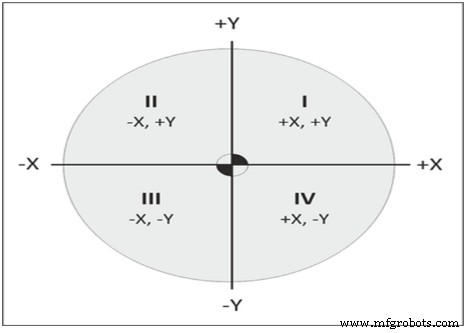
Рисунок 10
Четыре квадранта:
Когда мы включаем отрицательные значения, оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(Они нумеруются против часовой стрелки)

В квадранте I:и x, и y положительны
InQuadrant II:x неотрицательно (y все еще положительно)
InQuadrant III:и x, и y отрицательны
InQuadrant IV:x снова положительный, а y отрицательный
| Квадрант | X (по горизонтали) | Y (вертикально) | Пример |
| Я | Положительно | Положительно | (3,2) |
| II | Исключение | Положительно | (-5, 2) |
| III | Исключение | Отрицательный | (-2, -1) |
| IV | Положительно | Отрицательный | (2, -5) |
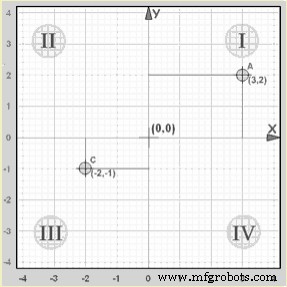
Пример:точка «А» (3,2) находится на 3 единицы по оси X и на 2 единицы вверх по оси Y.
И x, и y положительны, поэтому эта точка находится в «Квадранте I»
Пример. Точка "C" (-2,-1) находится на 2 единицы по оси X в отрицательном направлении и на 1 единицу вниз по оси Y в отрицательном направлении.
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Размеры:1, 2, 3 и более…
1. Строка с реальным числом может идти только:
- влево-вправо
- поэтому для любой позиции нужен только один номер
2. Декартовы координаты могут быть:
- влево-вправо и
- вверх-вниз
- поэтому для любой позиции нужно два числа
3. 3 параметра
- влево-вправо,
- вверх-вниз и
- вперед-назад
БЛОК-ТЕСТ
1. Что такое ЧПУ?
2. Опишите декартову систему координат.
3. Каково происхождение?
4. Горизонтальная линия как называется?
5. Вертикальная линия как называется?
6. Опишите числовую прямую.
7. Объясните абсциссу и ординату.
8. Каковы представления трех осей трехмерной декартовой системы координат.
9. Оси координат делят плоскость на четыре части, как называется?
10. В квадранте IV оси X и оси Y — это что?
Промышленные технологии
- Станок с ЧПУ
- Как использовать фрезерный станок с ЧПУ?
- Операции на токарных станках и режущие инструменты токарных станков
- Что такое строгальный станок? - определение, детали и типы
- Как искусственный интеллект и машинное обучение влияют на обработку с ЧПУ
- Противопожарная защита электроэрозионных станков и станков с ЧПУ:сравнение вариантов
- 22 Модуль 5:Работа с ЧПУ
- Повышение точности станка с ЧПУ и позиционирования
- Детали и элементы систем станков с ЧПУ
- G-коды и M-коды станков с ЧПУ – фрезерные и токарные станки с ЧПУ



