Закон тока и напряжения Кирхгофа (KCL и KVL) | Решенный пример

KCL и KVL — первый и второй законы Кирхгофа с решенным примером

Немецкий физик Роберт Кирхгоф в 1847 году ввел два важных электрических закона, с помощью которых мы можем легко найти эквивалентное сопротивление сложной сети и токов, протекающих в разных проводниках. Цепи переменного и постоянного тока можно решить и упростить, используя эти простые законы, известные как закон Кирхгофа для тока (KCL) и закон Кирхгофа для напряжения (KVL).

Также обратите внимание, что KCL выводится из уравнения непрерывности заряда в электромагнетизме, а KVL выводится из уравнения Максвелла – Фарадея для статического магнитного поля (производная B по времени равна 0 ).

Действующий закон Кирхгофа (KCL):

Согласно KCL:

В любой электрической сети алгебраическая сумма входящих токов в точку и исходящих токов из этой точки равна нулю. Или входящие токи в точку равны выходящим токам из этой точки.

Другими словами, сумма токов, текущих к точке, равна сумме токов, утекающих от нее. Или алгебраическая сумма токов, входящих в узел, равна алгебраической сумме токов, выходящих из него.

Объяснение KCL:

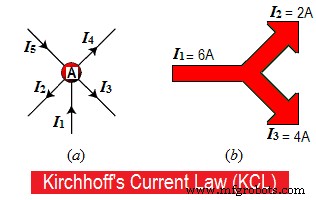
Предположим, что несколько проводников встречаются в точке «A», как показано на рис. 1.a. В одних проводниках токи входят в точку «А», а в других проводниках токи выходят или исходят из точки «А».

Рассматривайте входящие или входящие токи как «положительные (+) в направлении точки «А», а выходящие или исходящие токи из точки «А» — как «отрицательные (-)».<бр />тогда:

Я ₁ + (–Я ₂ ) + (–Я ₃ ) + (–Я ₄ ) + Я ₅ =0

ИЛИ

Я ₁ + Я ₅ – Я ₂ – Я ₃ – Я ₄ =0

ИЛИ

Я ₁ + Я ₅ =Я ₂ + Я ₃ + Я ₄ =0

т. е.

Входящие или входящие потоки =исходящие или исходящие потоки

Или

ΣЯ Ввод =ΣI Уход

Например, 8A приближается к точке, а 5A плюс 3A покидают эту точку на рис. 1.b, поэтому

8A =5A + 3A

8A =8A.

Закон Кирхгофа о напряжении (KVL):

Второй закон Кирхгофа или KVL утверждает, что;

Другими словами, в любом замкнутом контуре (известном также как Mesh) алгебраическая сумма приложенных ЭДС равна алгебраической сумме падений напряжения на элементах. . Второй закон Кирхгофа также известен как закон напряжения или закон сетки.

ΣIR=ΣE

Объяснение KVL:

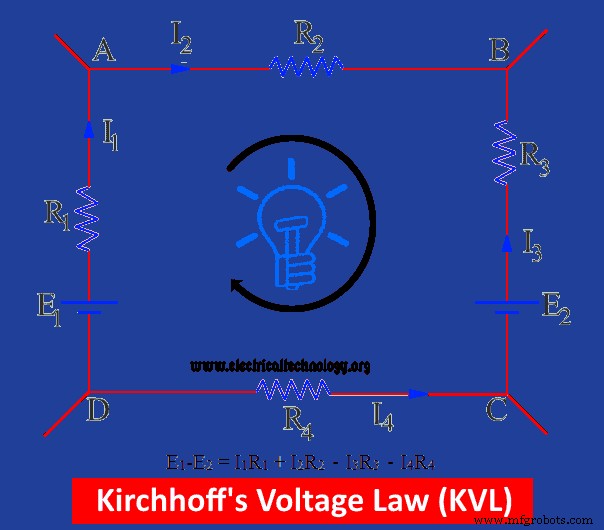
На рис. показана замкнутая цепь, содержащая два соединения батарей E₁ и Е₂ . Общая сумма ЭДС батарей обозначается как E₁ -Е₂ . Воображаемое направление тока также показано на рис.

E₁ управляет током в таком направлении, которое должно быть положительным, в то время как E₂ вмешивается в направлении тока (т. е. в направлении, противоположном предполагаемому направлению тока), следовательно, он считается отрицательным. Падение напряжения в этой замкнутой цепи зависит от произведения напряжения и тока.

Падение напряжения происходит в предполагаемом направлении тока и называется положительным падением напряжения, а другое — отрицательным падением напряжения.

На приведенном выше рисунке I₁ Р₁ и я₂ Р₂ положительные падения напряжения и I₃ Р₃ и я₄ Р₄ являются отрицательными V.D.

Если обойти замкнутую цепь (или каждую сетку) и умножить сопротивление проводника на протекающий в нем ток, то сумма IR будет равна сумма приложенных источников ЭДС, подключенных к цепи.

Общее уравнение для приведенной выше схемы:

E₁ – Е₂ =я ₁ Р₁ + я ₂ Р₂ – я ₃ Р₃ – я ₄ Р₄

Если мы движемся в предполагаемом направлении тока, как показано на рис., то произведение IR считается положительным, в противном случае - отрицательным.

Полезно знать:

Направление тока:

Очень важно определять направление тока при решении цепей по законам Кирхгофа. То же, что и в случае избирательного тока и обычного тока.

Направление тока можно принять по часовой стрелке или против часовой стрелки. После того, как вы выберете пользовательское направление тока, вам нужно будет применить и поддерживать то же направление для всей схемы до окончательного решения схемы.

Если мы получили положительное конечное значение, это означает, что предполагаемое направление тока было правильным. В случае отрицательных значений ток направления меняется на противоположный по сравнению с предполагаемым.

Анализ цепи по законам Кирхгофа

Пример решения KCL и KVL (законы Кирхгофа)

Пример:

Резисторы R₁ =10 Ом, R₂ =4 Ом и R₃ =8 Ом подключены к двум батареям (пренебрежимо малого сопротивления), как показано на рисунке. Найдите ток через каждый резистор.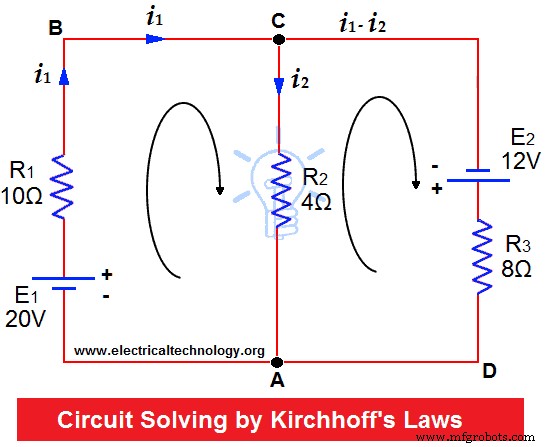

Решение:

Предположим, что течения текут в направлениях, указанных стрелками.

Примените KCL к перекресткам C и A.

Поэтому текущий в сетке ABC =i ₁

Current in Mesh CA =i ₂

Тогда current в Mesh CDA =i ₁ – я ₂

Теперь примените KVL к сетке ABC, 20 В действуют по часовой стрелке. Приравнивая сумму произведений IR, получаем;

10i ₁ + 4я ₂ =20   …   (1)

В сетке ACD 12 вольт действуют по часовой стрелке, тогда:

8(i ₁ – я ₂ ) – 4i ₂ =12

8i ₁ – 8я ₂ – 4я ₂ =12

8я ₁ – 12я ₂ =12   …   (2)

Умножение уравнения (1) на 3;

30i ₁ + 12я ₂ =60

Решение для i ₁

30i ₁ + 12я ₂ =60

8i ₁ – 12я ₂ =12

___________
38i ₁ =72

Приведенное выше уравнение также можно упростить с помощью исключения или правила Крамера.

i ₁ =72 ÷ 38 =1,895 Ампер =Ток в резисторе 10 Ом

Подставив это значение в (1), мы получим:

10 (1,895) + 4i ₂ =20

4i ₂ =20 – 18,95

i ₂ =0,263 Ампер =Ток в резисторах 4 Ом.

Теперь

i ₁ – я ₂ =1,895 – 0,263 =1,632 Ампер

Применение законов Кирхгофа

• Законы Кирхгофа можно использовать для определения значений неизвестных величин, таких как ток и напряжение, а также направления потоков значений этих квинтетов в цепи.
• Эти законы можно применить к любой схеме* (см. ограничения законов Кирхгофа в конце статьи), но они полезны для поиска неизвестных значений в сложных схемах и сетях.
• Также используется в узловом и сеточном анализе для определения значений тока и напряжения.
• Ток через каждый независимый контур передается путем применения KVL (каждого контура) и тока в любом элементе цепи путем подсчета всего тока (применимо в методе контурного тока).
• Ток через каждую ветвь передается путем применения KCL (каждого соединения) KVL в каждом контуре цепи (применяется в методе контурного тока).
• Законы Кирхгофа полезны для понимания передачи энергии по электрической цепи.

Полезно знать:

Эти практические правила необходимо учитывать при упрощении и анализе электрических цепей по законам Кирхгофа:

• Падение напряжения в контуре из-за прохождения тока по часовой стрелке считается положительным (+) падением напряжения.
• Падение напряжения в контуре из-за прохождения тока против часовой стрелки считается отрицательным (-) падением напряжения.
• Ток, получаемый от батареи по часовой стрелке, считается положительным (+).
• Ток, вырабатываемый батареей против часовой стрелки, считается положительным (-).

Ограничения законов Кирхгофа:

• KCL применим при условии, что ток течет только в проводниках и проводах. В то время как в высокочастотных цепях, где паразитную емкость больше нельзя игнорировать. В таких случаях ток может течь в разомкнутой цепи, потому что в этих случаях проводники или провода действуют как линии передачи.
• KVL применим при условии отсутствия флуктуирующего магнитного поля, связывающего замкнутый контур. В то время как при наличии изменяющегося магнитного поля в высокочастотных, но коротковолновых цепях переменного тока электрическое поле не является консервативным векторным полем. Итак, электрическое поле не может быть градиентом какого-либо потенциала и линейный интеграл электрического поля вокруг петли не равен нулю, что прямо противоречит КВЛ. Поэтому КВЛ в таких условиях неприменим.
• Во время передачи энергии от магнитного поля к электрическому, где выдумка должна быть введена в KVL, чтобы сделать P.d (разность потенциалов) по цепи равной 0.

Похожие статьи о теоремах анализа электрических цепей:

• Теорема Тевенина. Пошаговая процедура с решенным примером
• Теорема Нортона. Простая пошаговая процедура с примером (изображения)
• Анализ схемы SUPERNODE | Шаг за шагом с решенным примером
• Анализ цепей SUPERMESH | Шаг за шагом с решенным примером
• Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
• Теорема о компенсации — доказательство, объяснение и примеры решения
• Теорема о подстановке:пошаговое руководство с примером решения
• Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры
• Теорема о суперпозиции — анализ цепей с решенным примером
• Теорема Теллегена — Решенные примеры и моделирование в MATLAB
• Правило делителя напряжения (VDR) — примеры решений для цепей R, L и C
• Current Divider Rule (CDR) — решенные примеры для цепей переменного и постоянного тока
• Закон Ома:простое объяснение с утверждением и формулами
• Преобразование из звезды в дельту и из дельты в звезду. Преобразование Y-Δ