Последовательные схемы резистор-конденсатор

В последнем разделе мы узнали, что произойдет в простых цепях переменного тока, состоящих только из резисторов и только конденсаторов. Теперь мы последовательно объединим эти два компонента и исследуем эффекты.

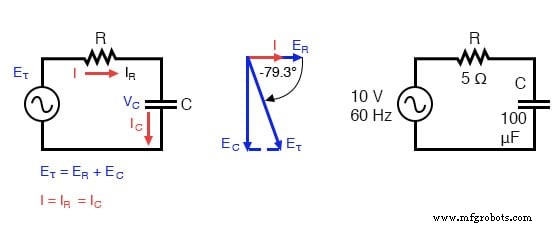
Цепь последовательного конденсатора:напряжение отстает от тока от 0 ° до 90 °.

Расчет импеданса

Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а конденсатор - 26,5258 Ом реактивного сопротивления переменному току при 60 Гц.

Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление конденсатора - мнимым числом (26,5258 Ом ∠ -90 ° или 0 - j26,5258 Ом), совокупный эффект двух компонентов будет противостоять току, равному комплексной сумме двух чисел.

Термин для этого сложного противодействия току - импеданс . , его символ - Z, и он также выражается в единицах Ом, как и сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:

Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:

Фактически, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E =IR), точно так же, как импеданс является гораздо более полным выражением сопротивления потоку электронов, чем простое сопротивление. Любое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно / параллельно), могут и должны быть представлены как единый импеданс.

Текущий расчет

Чтобы рассчитать ток в приведенной выше схеме, нам сначала нужно указать опорный фазовый угол для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивного и емкостного сопротивления всегда 0 ° и -90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока.)

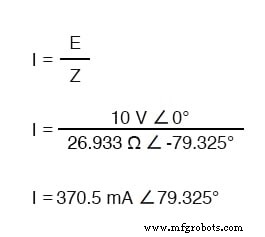
Как и в случае чисто емкостной схемы, волна тока опережает волну напряжения (источника), хотя на этот раз разница составляет 79,325 ° вместо полных 90 °.

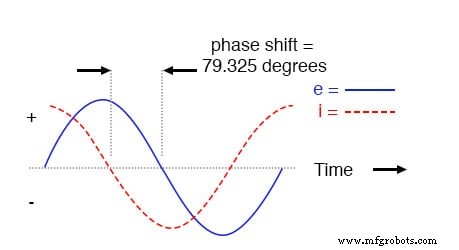
Напряжение отстает от тока (напряжение токопроводов) в последовательной цепи R-C.

Табличный метод

Как мы узнали из главы, посвященной индуктивности переменного тока, «табличный» метод организации параметров цепи является очень полезным инструментом для анализа переменного тока, так же как и для анализа постоянного тока. Поместим известные цифры для этой последовательной цепи в таблицу и продолжим анализ с помощью этого инструмента:

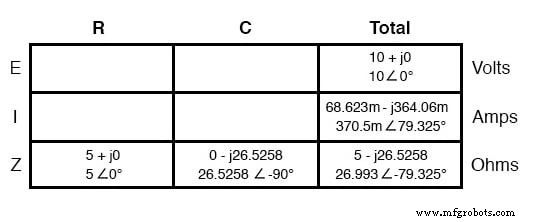
Ток в последовательной цепи равномерно распределяется между всеми компонентами, поэтому цифры, помещенные в столбец «Итого» для тока, могут быть распределены также и на все другие столбцы:

Продолжая наш анализ, мы можем применить закон Ома (E =IR) по вертикали, чтобы определить напряжение на резисторе и конденсаторе:

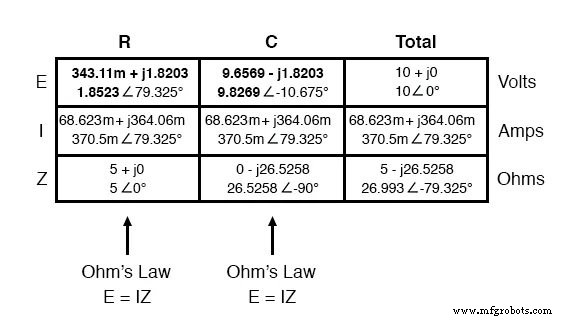
Обратите внимание на то, что напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора). Напряжение на конденсаторе имеет фазовый угол -10,675 °, что ровно на 90 ° меньше . чем фазовый угол тока в цепи. Это говорит нам о том, что напряжение и ток конденсатора все еще не совпадают по фазе на 90 ° друг с другом.

Расчеты с использованием SPICE

Давайте проверим наши расчеты с помощью SPICE:

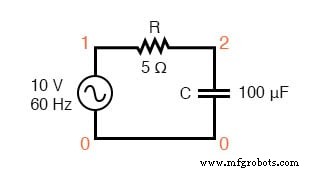
Схема для специй:R – C.

 ac r-c схема v1 1 0 ac 10 грех г1 1 2 5 c1 2 0 100u .ac lin 1 60 60 .print ac v (1,2) v (2,0) i (v1) .print ac vp (1,2) vp (2,0) ip (v1) .конец частота v (1,2) v (2) i (v1) 6.000E + 01 1.852E + 00 9.827E + 00 3.705E-01 частота вп (1,2) вп (2) ip (v1) 6.000E + 01 7.933E + 01 -1.067E + 01 -1.007E + 02 

И снова SPICE неправильно печатает текущий фазовый угол со значением, равным реальному фазовому углу плюс 180 ° (или минус 180 °).

Однако исправить эту цифру и проверить правильность нашей работы несложно. В этом случае значение -100,7 °, выдаваемое SPICE для текущего фазового угла, соответствует положительному значению 79,3 °, что соответствует ранее рассчитанному нами значению 79,325 °.

Опять же, необходимо подчеркнуть, что расчетные значения, соответствующие реальным измерениям напряжения и тока, приведены в полярных форма, а не прямоугольная форма!

Например, если бы мы действительно построили эту последовательную цепь резистор-конденсатор и измерили напряжение на резисторе, наш вольтметр показал бы 1.8523 вольт, а не 343,11 милливольта (действительный прямоугольник) или 1,8203 вольт (воображаемый прямоугольник).

Реальные приборы, подключенные к реальным цепям, дают показания, соответствующие длине вектора (величине) вычисленных значений. Хотя прямоугольная форма записи комплексных чисел полезна для выполнения сложения и вычитания, это более абстрактная форма записи, чем полярная, которая сама по себе имеет прямое соответствие с истинными измерениями.

Импеданс (Z) последовательной цепи R-C может быть вычислен с учетом сопротивления (R) и емкостного реактивного сопротивления (X _C ). Поскольку E =IR, E =IX _C , и E =IZ, сопротивление, реактивное сопротивление и импеданс пропорциональны напряжению соответственно. Таким образом, векторная диаграмма напряжения может быть заменена аналогичной диаграммой импеданса.

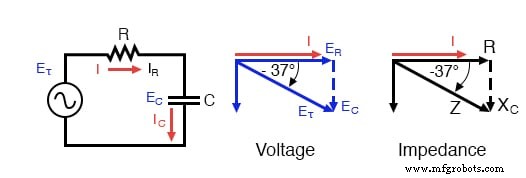
Серия:векторная диаграмма импеданса цепи R-C .

Пример: Дано:резистор 40 Ом последовательно с конденсатором на 88,42 мкФ. Найдите полное сопротивление 60 Гц.

 XC =1 / (2πfC) XC =1 / (2π · 60 · 88,42 × 10-6) XC =30 Ом Z =R - jXC Z =40 - j30 | Z | =sqrt (402 + (-30) 2) =50 Ом ∠Z =арктангенс (-30/40) =-36,87 ° Z =40 - j30 =50∠-36,87 ° 

ОБЗОР:

• Импеданс представляет собой общую меру сопротивления электрическому току и представляет собой комплексную (векторную) сумму («реального») сопротивления и («мнимого») реактивного сопротивления.
• Импедансом (Z) управляют так же, как и сопротивлением (R) при анализе последовательной цепи:последовательное сопротивление складывается для формирования общего импеданса. Только обязательно выполняйте все вычисления в сложной (не скалярной) форме! Z _Total1 + Z ₂ +. . . Z _n
• Обратите внимание, что импедансы всегда добавляются последовательно, независимо от того, какой тип компонентов составляет импеданс. То есть резистивный импеданс, индуктивный импеданс и емкостной импеданс следует рассматривать одинаково математически.
• У чисто резистивного импеданса всегда будет фазовый угол точно 0 ° (Z _R =R Ω ∠ 0 °).
• Чисто емкостное сопротивление всегда будет иметь фазовый угол точно -90 ° (Z _C =X _C Ω ∠ -90 °).
• Закон Ома для цепей переменного тока:E =IZ; I =E / Z; Z =E / I
• Когда резисторы и конденсаторы смешиваются в цепях, общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица последовательных и параллельных цепей переменного тока