Параллельные схемы резистор-конденсатор

Используя компоненты с одинаковыми значениями в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:

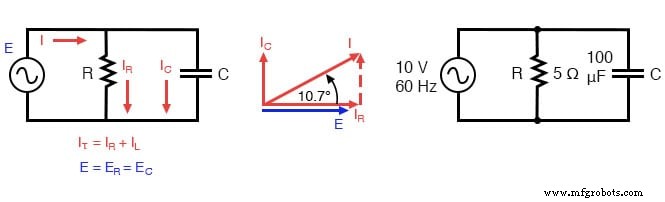
Параллельная R-C цепь.

Резистор и конденсатор параллельно

Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу аналитическую таблицу с теми же «заданными» значениями:

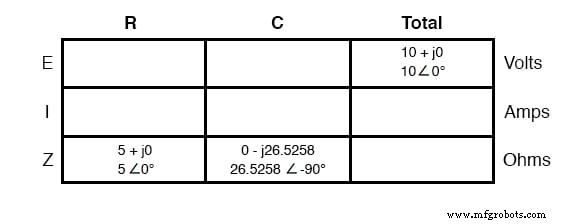
Поскольку теперь это параллельная схема, мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт 0 °) во все столбцы:

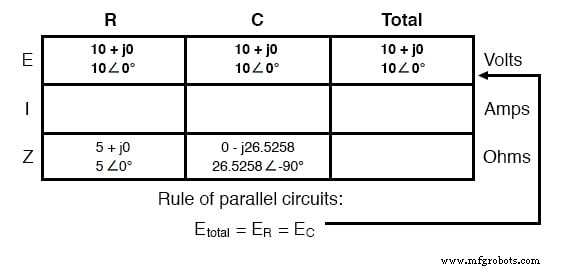
Расчет с использованием закона Ома

Теперь мы можем применить закон Ома (I =E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через конденсатор:

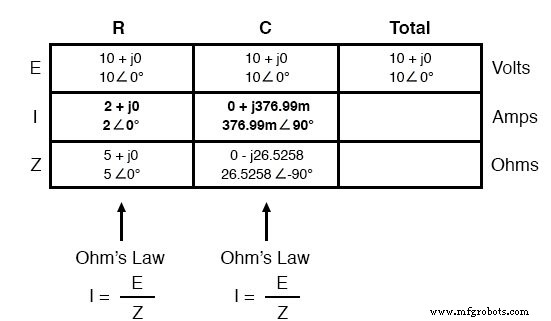
Как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):

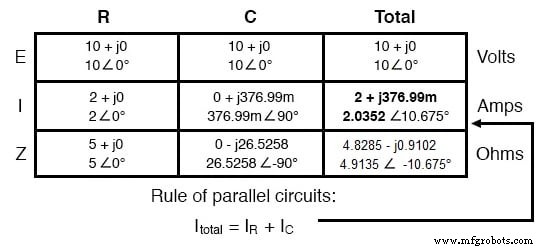
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z =E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, аналогичную той, которая используется при вычислении параллельных сопротивлений.

Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.

Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации:в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле.

И снова формула параллельного импеданса выглядит так:

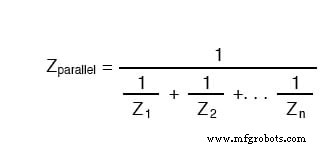
Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами. Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы придем к одному и тому же значению:

ОБЗОР:

• Импедансом (Z) управляют так же, как сопротивлением (R) при анализе параллельной цепи:параллельные импедансы уменьшаются, чтобы сформировать общий импеданс, используя обратную формулу. Только обязательно выполняйте все вычисления в сложной (не скалярной) форме! ZTotal =1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
• Закон Ома для цепей переменного тока:E =IZ; I =E / Z; Z =E / I
• Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °. Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
• Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока:напряжение равномерно по всей цепи, токи ответвления складываются, образуя общий ток, а импедансы уменьшаются (по обратной формуле), образуя общий импеданс.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица последовательных и параллельных цепей переменного тока