Резонанс в последовательно-параллельных цепях

В простых реактивных схемах с небольшим сопротивлением или без него эффекты радикально измененного импеданса будут проявляться на резонансной частоте, предсказанной уравнением, приведенным ранее. В параллельном (резервуарном) LC-контуре это означает бесконечное сопротивление при резонансе. В последовательном LC-контуре это означает нулевой импеданс при резонансе:

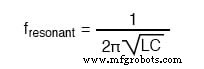
Однако, как только в большинство контуров LC вводятся значительные уровни сопротивления, этот простой расчет резонанса становится недействительным.

На этой странице мы рассмотрим несколько LC-цепей с добавленным сопротивлением, используя те же значения емкости и индуктивности, что и раньше:10 мкФ и 100 мГн соответственно.

Расчет резонансной частоты цепи с высоким сопротивлением

Согласно нашему простому уравнению, приведенному выше, резонансная частота должна быть 159,155 Гц. Однако посмотрите, где ток достигает максимума или минимума, в следующих анализах SPICE:

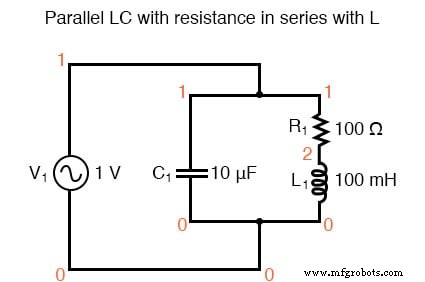
Параллельная LC-цепь с сопротивлением последовательно с L.

 резонансный контур v1 1 0 ac 1 грех c1 1 0 10u г1 1 2 100 l1 2 0 100м .ac lin 20 100 200 .plot ac i (v1) .конец 

Результаты:

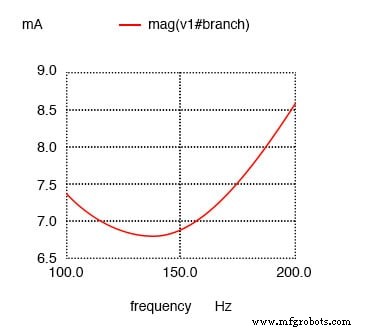
Сопротивление последовательно с L дает минимальный ток при 136,8 Гц вместо расчетных 159,2 Гц

 Минимальный ток при 136,8 Гц вместо 159,2 Гц! 

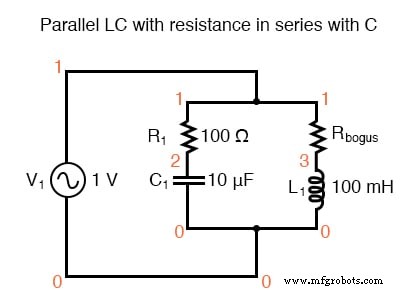
Параллельный LC с сопротивлением в серии с C.

Здесь требуется дополнительный резистор (Rbogus), чтобы SPICE не столкнулся с проблемами при анализе. SPICE не может работать с индуктором, подключенным напрямую параллельно любому источнику напряжения или любому другому индуктору, поэтому добавление последовательного резистора необходимо для «разрыва» цепи источника напряжения / индуктора, которая в противном случае образовалась бы.

Этот резистор выбран как очень низкое значение для минимального воздействия на поведение цепи.

 резонансный контур v1 1 0 ac 1 грех г1 1 2 100 c1 2 0 10u rbogus 1 3 1e-12 l1 3 0 100м .ac lin 20 100 400 .plot ac i (v1) .конец 

 Минимальный ток примерно при 180 Гц вместо 159,2 Гц! 

Результаты:

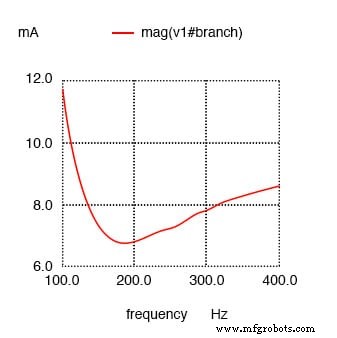
Сопротивление последовательно с C сдвигает минимальный ток с расчетных 159,2 Гц до примерно 180 Гц.

Цепи серии LC

Обращая внимание на последовательные LC-цепи, мы экспериментируем с размещением значительных сопротивлений параллельно L или C. В следующих примерах последовательной цепи резистор 1 Ом (R1) включен последовательно с катушкой индуктивности и конденсатором для ограничения общего тока на резонанс.

«Дополнительным» сопротивлением, добавленным для воздействия на эффекты резонансной частоты, является резистор R2 сопротивлением 100 Ом. Результаты показаны на рисунке ниже.

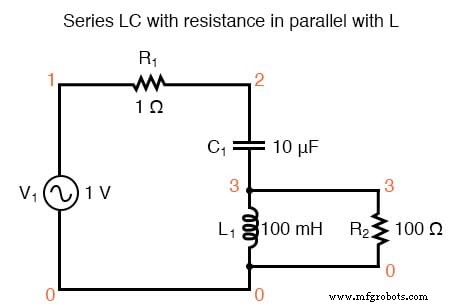
Резонансный контур последовательного LC с сопротивлением, параллельным L.

 резонансный контур v1 1 0 ac 1 грех г1 1 2 1 c1 2 3 10u l1 3 0 100м г2 3 0100 .ac lin 20 100 400 .plot ac i (v1) .конец 

 Максимальный ток примерно при 178,9 Гц вместо 159,2 Гц! 

Результаты:

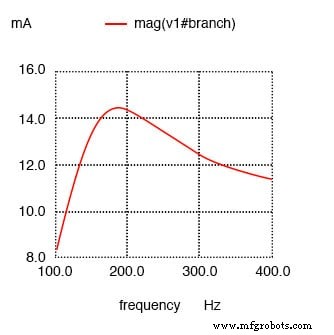
Последовательный резонансный контур с сопротивлением, параллельным L, сдвигает максимальный ток с 159,2 Гц до примерно 180 Гц.

И, наконец, последовательный LC-контур со значительным сопротивлением параллельно конденсатору. Сдвинутый резонанс показан ниже.

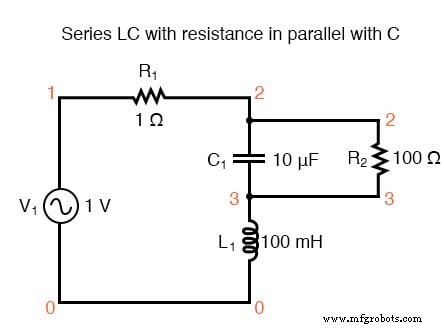
Резонансный контур последовательного LC с сопротивлением, параллельным C.

 резонансный контур v1 1 0 ac 1 грех г1 1 2 1 c1 2 3 10u г2 2 3 100 l1 3 0 100м .ac lin 20 100 200 .plot ac i (v1) .конец 

 Максимальный ток при 136,8 Гц вместо 159,2 Гц! 

Результаты:

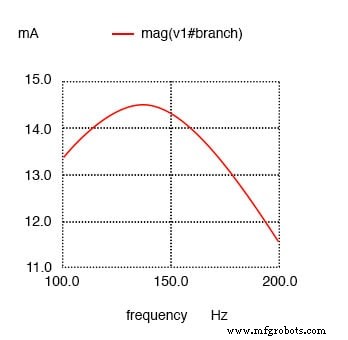
Сопротивление, параллельное C в последовательном резонансном контуре, смещает максимум тока с расчетных 159,2 Гц до примерно 136,8 Гц.

Антирезонанс в цепях LC

Тенденция дополнительного сопротивления к перекосу точки, в которой импеданс достигает максимума или минимума в цепи LC, называется антирезонансом . . Проницательный наблюдатель заметит закономерность между четырьмя приведенными выше примерами SPICE с точки зрения того, как сопротивление влияет на резонансный пик цепи:

Параллельный («резервуарный») LC-контур:

• R последовательно с L:резонансная частота смещена вниз
• R последовательно с C:резонансная частота сдвинута вверх

Последовательная LC-цепь:

• R параллельно L:резонансная частота сдвинута вверх
• R параллельно с C:резонансная частота сдвинута вниз

Опять же, это иллюстрирует взаимодополняющий характер конденсаторов и катушек индуктивности:как сопротивление, включенное последовательно с одним, создает антирезонансный эффект, эквивалентный сопротивлению, подключенному параллельно с другим. Если вы посмотрите еще ближе к четырем приведенным примерам SPICE, вы увидите, что частоты сдвинуты на одинаковую величину . , и что формы дополнительных графов являются зеркальным отображением друг друга!

Антирезонанс - это эффект, о котором должны знать разработчики резонансных цепей. Уравнения для определения «сдвига» антирезонанса сложны и не будут рассматриваться в этом кратком уроке. Начинающему студенту электроники должно быть достаточно понять, что эффект существует и каковы его общие тенденции.

Кожный эффект

Дополнительное сопротивление в цепи LC - не академический вопрос. Хотя можно производить конденсаторы с незначительным нежелательным сопротивлением, индукторы обычно имеют значительное сопротивление из-за большой длины проводов, используемых в их конструкции.

Более того, сопротивление провода имеет тенденцию увеличиваться с увеличением частоты из-за странного явления, известного как скин-эффект где переменный ток, как правило, не проходит через самый центр провода, тем самым уменьшая эффективную площадь поперечного сечения провода.

Таким образом, катушки индуктивности не только имеют сопротивление, но и изменяются, частотно-зависимые . сопротивление при этом.

Добавленное сопротивление в цепях

Как будто сопротивления провода катушки индуктивности недостаточно, чтобы вызвать проблемы, мы также должны бороться с «потерями в сердечнике» катушек индуктивности с железным сердечником, которые проявляются как дополнительное сопротивление в цепи.

Поскольку железо является проводником электричества, а также магнитного потока, изменение потока, создаваемого переменным током, протекающим через катушку, будет вызывать электрические токи в самом сердечнике ( вихревые токи ).

Этот эффект можно представить, как если бы железный сердечник трансформатора был своего рода вторичной обмоткой трансформатора, питающей резистивную нагрузку:неидеальная проводимость металлического железа. Этот эффект можно свести к минимуму с помощью ламинированных сердечников, высококачественных материалов с хорошей конструкцией сердечника, но полностью исключить их невозможно.

Цепи RLC

Одним заметным исключением из правила сопротивления цепи, вызывающего сдвиг резонансной частоты, является случай цепей последовательно резистор-индуктор-конденсатор («RLC»). Пока все компоненты соединены последовательно друг с другом, сопротивление не влияет на резонансную частоту контура. Полученный график показан ниже.

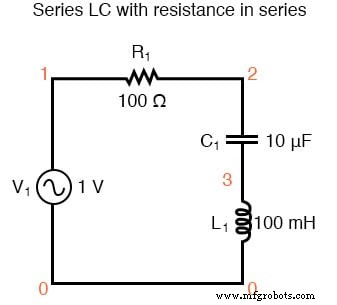
Последовательный ЖК с последовательным сопротивлением.

 последовательная цепь rlc v1 1 0 ac 1 грех г1 1 2 100 c1 2 3 10u l1 3 0 100м .ac lin 20 100 200 .plot ac i (v1) .конец 

 И снова максимальный ток при 159,2 Гц! 

Результаты:

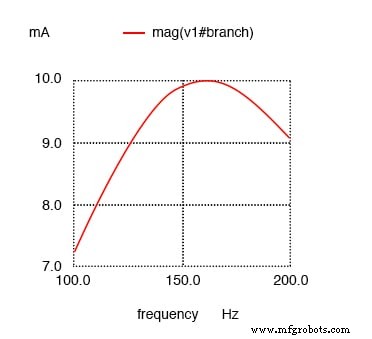
Сопротивление в последовательном резонансном контуре оставляет максимальный ток на расчетном уровне 159,2 Гц, расширяя кривую.

Обратите внимание, что пик на графике тока не изменился по сравнению с более ранней последовательной LC-схемой (той, в которой было сопротивление токена 1 Ом), хотя сопротивление теперь в 100 раз больше. Единственное, что изменилось, - это «резкость» кривой.

Очевидно, что эта цепь не так сильно резонирует, как схема с меньшим последовательным сопротивлением (она называется «менее избирательной»), но, по крайней мере, она имеет такую ​​же собственную частоту!

Демпфирующий эффект антирезонанса

Примечательно, что антирезонанс имеет эффект гашения колебаний автономных LC-контуров, таких как контуры резервуара. В начале этой главы мы увидели, как конденсатор и катушка индуктивности, соединенные напрямую вместе, будут действовать как маятник, обмениваясь пиками напряжения и тока, точно так же, как маятник обменивается кинетической и потенциальной энергией.

В идеальном контуре резервуара (без сопротивления) это колебание будет продолжаться вечно, точно так же, как маятник без трения продолжит вечно качаться на своей резонансной частоте. Но машины без трения трудно найти в реальном мире, как и схемы танков без потерь.

Энергия, теряемая через сопротивление (или потери в сердечнике индуктора, или излучаемые электромагнитные волны, или ...) в контуре резервуара, вызовет затухание колебаний по амплитуде до тех пор, пока они не исчезнут. Если в контуре резервуара присутствует достаточное количество потерь энергии, он вообще не сможет резонировать.

Демпфирующий эффект антирезонанса - это больше, чем просто любопытство:его можно довольно эффективно использовать для устранения нежелательных колебания в цепях, содержащих паразитные индуктивности и / или емкости, как это происходит почти во всех цепях. Обратите внимание на следующую схему задержки времени L / R:(рисунок ниже)

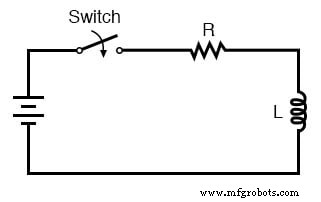
Схема задержки времени L / R

Идея этой схемы проста:«заряжать» катушку индуктивности при замкнутом переключателе. Скорость зарядки индуктора будет установлена ​​соотношением L / R, которое представляет собой постоянную времени цепи в секундах.

Однако, если вы построите такую ​​схему, вы можете обнаружить неожиданные колебания (переменного тока) напряжения на катушке индуктивности, когда переключатель замкнут. (Рисунок ниже) Почему это? В цепи нет конденсатора, так как же мы можем получить резонансные колебания, используя только катушку индуктивности, резистор и аккумулятор?

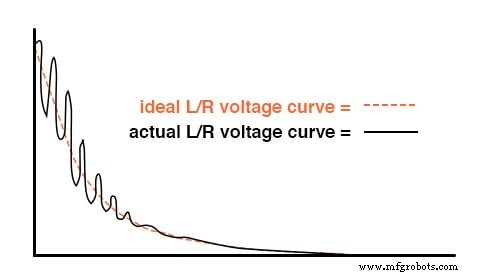
Звон индуктивности из-за резонанса с паразитной емкостью.

Все катушки индуктивности содержат определенную паразитную емкость из-за межвитковых и межвитковых изоляционных промежутков. Кроме того, размещение проводников схемы может создать паразитную емкость. Хотя чистая компоновка схемы важна для устранения большей части этой паразитной емкости, всегда будут такие, которые вы не сможете устранить.

Если это вызывает резонансные проблемы (нежелательные колебания переменного тока), дополнительное сопротивление может быть способом борьбы с ними. Если резистор R достаточно велик, это вызовет состояние антирезонанса, рассеивая достаточно энергии, чтобы индуктивность и паразитная емкость не могли поддерживать колебания в течение очень длительного времени.

Интересно, что принцип использования сопротивления для устранения нежелательного резонанса часто используется при проектировании механических систем, где любой движущийся объект с массой является потенциальным резонатором.

Очень распространенное применение этого - использование амортизаторов в автомобилях. Без амортизаторов автомобили будут сильно подпрыгивать на своей резонансной частоте после столкновения с любой неровностью на дороге. Работа амортизатора заключается в создании сильного антирезонансного эффекта за счет гидравлического рассеивания энергии (так же, как резистор рассеивает энергию электрически).

ОБЗОР:

• Дополнительное сопротивление LC-цепи может вызвать состояние, известное как антирезонанс . , где эффекты пикового импеданса возникают на частотах, отличных от той, которая дает равные емкостное и индуктивное сопротивление.
• Сопротивление, присущее реальным катушкам индуктивности, может в значительной степени способствовать возникновению антирезонанса. Одним из источников такого сопротивления является скин-эффект . , вызванные исключением переменного тока из центра проводников. Другой источник - потери в сердечнике . в индукторах с железным сердечником.
• В простой последовательной LC-цепи, содержащей сопротивление (RLC-цепь), сопротивление не производят антирезонанс. Резонанс все еще возникает, когда емкостное и индуктивное сопротивление равны.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист резонанса