Определение характеристик деформации скольжения и нанометрической обрабатываемости монокристалла 6H-SiC в атомном масштабе

Введение

Как полупроводниковый материал третьего поколения с широкой запрещенной зоной, SiC обладает характеристиками высокого поля пробоя, высокой радиационной стойкостью, высокой скоростью насыщения носителей, быстрой теплопроводностью, малой диэлектрической проницаемостью и устойчивыми химическими свойствами, поэтому он имеет широкое применение в различных областях. высокотемпературных, высокочастотных, мощных, антирадиационных и коротковолновых оптоэлектронных устройств и оптоэлектронной интеграции [1].

Наиболее распространенными кристаллами SiC являются 3C, 4H и 6H. Такие методы обработки, как шлифование / притирка / полировка, по-прежнему являются основными методами обработки монокристаллического SiC. Однако соотношение твердости алмаза и SiC близко к 2:1 (глубина обработки <50 нм)), что намного ниже рекомендуемого значения 5:1 для процесса обработки [2]. Сильный износ режущего инструмента и внутренние повреждения напрямую влияют на качество пластины. Чтобы решить эти проблемы, была проделана большая работа, чтобы понять поведение SiC при удалении на наноуровне. Механизм удаления 3C-SiC и влияние факторов обработки были тщательно изучены, такие как механизм пластической деформации в процессе резания [3,4,5,6,7], износ инструмента [8], поведение трения [9] ], анизотропия 3C-SiC [10] и влияние температур резания [11].

6H-SiC имеет более сложную стопочную структуру ABCACB. Хотя механизм удаления 6H-SiC при обработке SPDT (одноточечное алмазное точение) (например, влияние переднего угла инструмента на процесс снятия материала [12] и переход от хрупкого к пластичному состоянию [13]) изучается, исследования, очевидно, являются менее 3C-SiC. Ширина запрещенной зоны 6H-SiC (3 эВ) явно выше, чем у 3C-SiC (2.3 эВ). В настоящее время технологический уровень процесса выращивания стержней из 6H-SiC намного выше, чем у 3C-SiC. 6H-SiC гораздо чаще используется в промышленности, чем 3C-SiC. Соответствующие устройства применялись в высокочастотных, мощных и высокотемпературных полях, такие как выпрямитель Шоттки, тиратрон и силовой MOSFET (полевой транзистор металл-оксид-полупроводник). Для повышения качества обработанной поверхности / подповерхности 6H-SiC наиболее эффективным и действенным средством в настоящее время является поиск подходящей комбинации плоскости кристалла (обрабатываемой поверхности) / ориентации кристалла (направления обработки), которая больше подходит для процесса 6H. -SiC.

Скретч-эксперимент и моделирование - одни из наиболее распространенных и эффективных методов изучения поведения удаления [14, 15]. Исследование механизма удаления материала в процессе царапания имеет большое руководящее значение для самого процесса абразивной обработки. Метод молекулярной динамики может обеспечить процесс образования и удаления повреждений в наномасштабе. Поэтому моделирование царапания методом молекулярной динамики было использовано для анализа поведения удаления 6H-SiC под влиянием кристаллографической анизотропии.

Методология

Моделирование резки в этой статье было выполнено с использованием крупномасштабного атомно-молекулярного массово-параллельного симулятора (LAMMPS) [16]. OIVTO [17] и метод идентификации структуры алмаза [18] использовались для визуализации модели и идентификации дефектов в этом исследовании. Реализации моделирования деталей и инструментов зависели от LAMMPS без помощи другого программного обеспечения. Как показано на рис. 1a – c, и заготовка, и инструмент были установлены как деформируемые тела, и во время моделирования исследовалось поведение износа. Модель инструмента и детали были разделены на три части:пограничный атомный слой, термостатический атомный слой и зона ньютоновских атомов. Чтобы заготовка оставалась в исходном положении, атомы пограничного слоя в нижнем и правом конце заготовки были закреплены. Атомы в слое термостата и слое Ньютона подчиняются второму закону Ньютона. Была применена периодическая граница по y направление. Перед симуляцией царапания модели были расслаблены ансамблем NVE с методом термостата Берендсена. Перед моделированием царапания применялся период релаксации 50 пс для получения устойчивого энергетического состояния. Форма абразива представляет собой сферическую корону треугольной пирамиды с углом между кромками 90 °. Как показано на рис. 2, обычные кристаллические плоскости (a-плоскость (базисная плоскость), m-плоскость (призматическая плоскость) и c-плоскость) для 6H-SiC были выбраны в качестве обрабатываемых поверхностей. Учитывая симметрию конструкции, в качестве поверхности обработки / направления обработки были выбраны следующие комбинации плоскости / ориентации:\ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline { 1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \). Параметры обработки моделирования показаны в Таблице 1. Перед моделированием царапания абразивные материалы размещались на левой стороне заготовки, а абразивный наконечник находился на 50 Å ниже верхней поверхности заготовки. Ближайшее расстояние между абразивом и заготовкой составляет 30 Å, что далеко от диапазона отсечки потенциала взаимодействия. Абразив движется от свободного конца заготовки в положительном направлении на x ось и завершите процесс царапания.

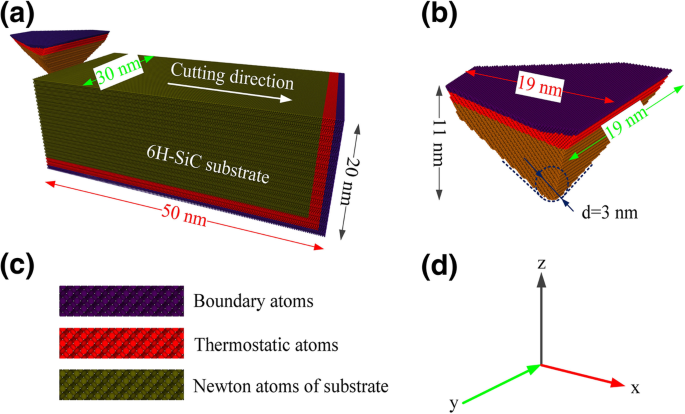
а МД-модель моделирования наноцарапания. б Морфология инструмента. c Состав модели. г Направление оси

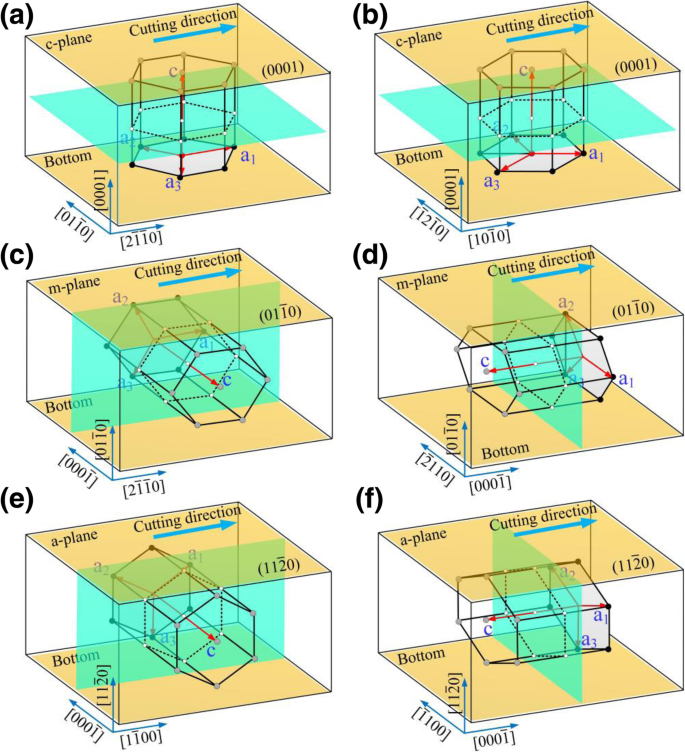
Принципиальная схема процесса царапания, где а - е - соответствующие режимы процесса \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) соответственно

Функция атомного потенциала играет решающую роль в точности и надежности моделирования молекулярной динамики. Согласно предыдущим испытаниям и моделированию механических свойств и механизмов удаления монокристаллического SiC, аналитическая функция потенциала порядка связи (ABOP), предложенная Эрхартом и Альбе [19], больше подходит для взаимодействий кремния и углерода. Параметры, используемые в потенциальной функции, показаны в таблице 2 [19]. Вместо функции потенциальной энергии Терсоффа [6], потенциальная функция ABOP используется для определения взаимодействий Si-Si, CC и Si-C внутри и между инструментом и заготовкой во время обработки [2, 7, 8, 10, 11].

Результаты и обсуждение

Нанометрический анализ обрабатываемости

Как показано на фиг. 3 и 4, анизотропия 6H-SiC оказала значительное влияние на нанометрическую обрабатываемость (глубину обработки, режим удаления, объем удаления, глубину подповерхностного повреждения (SSD) и т. Д.). В соответствии с соотношением между обрабатываемой поверхностью / направлением обработки и базовой плоскостью / c -оси (см. рис. 3), режимы обработки материала можно разделить на три категории:(i) базисная плоскость выбрана в качестве обрабатываемой поверхности, (ii) базальная плоскость перпендикулярна обрабатываемой поверхности и c -ось перпендикулярна направлению обработки, и (iii) c - ось параллельна направлению обработки.

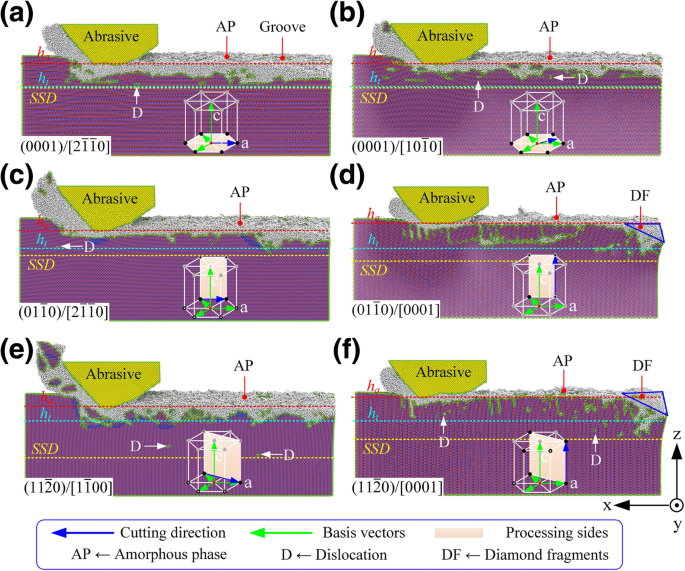
Топография обработанной поверхности при различных условиях кристаллической плоскости / ориентации, где a - е - соответствующие режимы процесса \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) соответственно

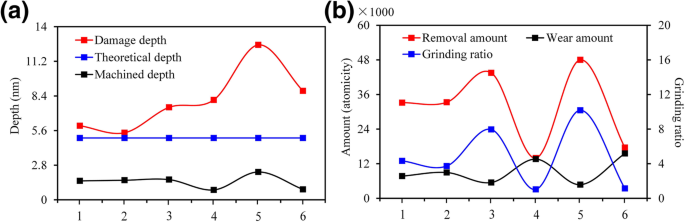
Нанометрическая обрабатываемость при различных условиях кристаллической плоскости / ориентации, a влияние анизотропии на глубину обработки и глубину повреждения, b влияние анизотропии на степень снятия, степень износа и коэффициент измельчения. 1, 2, 3, 4, 5 и 6 - соответствующие методы процесса \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) соответственно. Под глубиной поврежденного слоя понимается максимальная глубина внутренних дефектов кристалла, вызванных царапанием. Теоретическая глубина относится к заданной глубине перед обработкой. Под глубиной обработки понимается остаточная глубина после царапания. Величина удаления относится к количеству атомов, из которых удаляется материал детали. Степень износа означает разницу в количестве атомов абразивных зерен до и после царапания.

(i) Как показано на рис. 3a, b, нанометрическая обрабатываемость 6H-SiC была очень похожей, когда режим обработки был выбран как \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). Однако процесс удаления 6H-SiC был более склонен к хрупкому режиму, когда режим обработки был выбран как \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). (ii) Как показано на рис. 3c, e, когда режимы обработки были выбраны как \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), глубина обработки и объем снятия материала были значительно выше, чем в других методах обработки. Как показано на рис. 4, при той же теоретической глубине обработки ( h _т =5,0 нм) скорость съема материала в режиме обработки \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) была в 3,4 раза больше, чем что в режиме обработки \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \). Коэффициент обработки материала (количество снятого материала / износ инструмента) составлял 10,1, но SSD при этом параметре обработки также был намного выше, чем при других условиях обработки, достигая 2,3 раза от \ ((0001) / \ left [10 \ overline { 1} 0 \ справа] \). На обработанных поверхностях и сколах имеется большое количество нанокристаллитов. В этом состоянии произошло большое количество хрупких отказов. Режим обработки \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) подходит только для обработки наноканавок, которая требует высокой эффективности обработки, но нечувствительна к подземное повреждение. Скорость съема материала \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) была аналогична скорости съема \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), но SSD был только на 50% от последнего. Кроме того, толщина аморфного слоя на обработанной поверхности была намного меньше, чем у \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). Распределение подповерхностной фазы было равномерным, а механические свойства всей канавки были лучше, чем при других методах обработки. Таким образом, режим обработки \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) является лучшим выбором для обработки микронанавок на поверхности 6H-SiC с высокой эффективностью. , высокая точность и низкий SSD. (iii) Как показано на фиг. 3d, f, когда направление обработки было параллельно c -оси наконечник был сильно изношен на начальном этапе обработки. Хотя глубина обработки и скорость съема материала были намного ниже, чем при других методах обработки, а коэффициент обработки материала составлял всего около 1,0, SSD равнялся \ (\ left (01 \ overline {1} 0 \ right) / \ left [ 0001 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) режимы обработки были больше, чем режимы \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \). Следовательно, не рекомендуется использовать \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) при обработке микронанавок на поверхности 6H-SiC. Однако эти режимы демонстрируют отличную износостойкость; поэтому они подходят для передней поверхности режущего инструмента из монокристалла SiC, который имеет широкие перспективы в области сверхточной обработки черных металлов.

Анализ движения губ и распределения подповерхностных повреждений

Распределение факторов Шмида в процессе царапанья на основе вершины треугольной пирамиды

Общие системы скольжения гексагональной кристаллической системы (см. Рис. 4,) в первую очередь включают базальное скольжение, призматическое скольжение и пирамидальное скольжение. Сопротивление скольжению связано с обобщенной энергией дефекта упаковки (GSF) и d E _GSF / d x vs. ( x / b ) систем скольжения. Движение скольжения будет происходить по самой плотной плоскости и по кратчайшему направлению [10]. Предпочтительными системами скольжения в базальном скольжении являются базальное скольжение (перемешанные наборы) / <\ (1 \ overline {1} 00 \)> и базальное скольжение (перемешанные наборы) / <\ (11 \ overline {2} 0 \)> [20]. Поскольку в первом отсутствует промежуточный минимум энергии, последний имеет приоритет при моделировании и экспериментах [20]. Следовательно, движения скольжения, рассматриваемые в этой работе, следующие:базальное скольжение (перемешивание множеств) / <\ (11 \ overline {2} 0 \)> и призматическое скольжение и скольжение. Рис. 5.

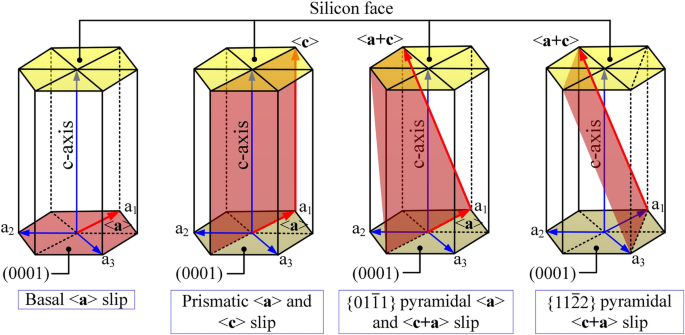
Системы скольжения гексагональной системы

Составляющая касательного напряжения на плоскости скольжения τ _сс можно рассчитать по соотношению:

$$ {\ tau} _ {\ mathrm {ss}} ={\ sigma} _ {\ mathrm {cont}} \ mathit {\ cos} <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {n_g}> \ cos <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {t_g}> ={\ sigma} _ {\ mathrm {cont}} \ bullet m $$ (1)

где σ _cont - контактное напряжение, \ (\ overset {\ rightharpoonup} {f} \) - направление нагрузки, \ (\ overset {\ rightharpoonup} {n_g} \) и \ (\ overset {\ rightharpoonup} {t_g} \) - нормаль к плоскости скольжения и направление скольжения в глобальной декартовой системе координат и m фактор Шмида. Глобальная система координат была фиксированной, а локальная система координат вращалась вместе с направлением кристалла. x -ось локальной системы координат была параллельна основному вектору \ (\ overset {\ rightharpoonup} {a_1} \), а z -ось параллельна основному вектору \ (\ overset {\ rightharpoonup} {c} \).

Во время процесса царапания первичной контактной поверхностью вершины треугольной пирамиды была передняя поверхность, но когда инструмент сильно изнашивался, основная контактная поверхность переходила на соединение передней поверхности и вершины вершины. Соответствующее направление нагрузки \ (\ overset {\ rightharpoonup} {f} \) представлено как

$$ \ left \ {\ begin {array} {c} \ overset {\ rightharpoonup} {f_1} =\ left ({f} _ {1x}, {f} _ {1y}, {f} _ {1z} \ right) \ kern8em \ mathrm {rake} \ \ mathrm {face} \ \\ {} \ overset {\ rightharpoonup} {f_2} =\ left ({f} _ {2x}, {f} _ {2y}, {f} _ {2z} \ right) \ kern9.75em \ mathrm {tip} \ \ mathrm {top} \ end {array} \ right. $$ (2)

где \ (\ overset {\ rightharpoonup} {f_1} =\ left (1,0, - \ sqrt {2} \ right) \), \ (\ overset {\ rightharpoonup} {f_2} =\ left (0,0 , -1 \ right) \) в глобальной системе координат.

Как гексагональная кристаллическая система, система скольжения 6H-SiC может быть выражена как { h k i l } / < у в т ш >. Нормаль плоскости скольжения \ (\ overset {\ rightharpoonup} {n_c} \) и направление скольжения \ (\ overset {\ rightharpoonup} {t_c} \) в локальной декартовой системе координат показаны как

$$ \ overset {\ rightharpoonup} {n_c} =\ left (\ frac {3} {2} h, \ frac {\ sqrt {3}} {2} \ left (h + 2k \ right), \ frac { 3 la} {2c} \ right) $$ (3) $$ \ overset {\ rightharpoonup} {t_c} =\ left (u- \ frac {1} {2} \ left (v + t \ right), \ frac {\ sqrt {3}} {2} \ left (vt \ right), \ frac {c} {a} w \ right) $$ (4)

Нормаль плоскости скольжения \ (\ overset {\ rightharpoonup} {n_g} \) и направление скольжения \ (\ overset {\ rightharpoonup} {t_g} \) в глобальной декартовой системе координат показаны как

$$ \ overset {\ rightharpoonup} {n_g} =T \ bullet \ overset {\ rightharpoonup} {n_c} $$ (4) $$ \ overset {\ rightharpoonup} {t_g} =T \ overset {\ rightharpoonup} {\ пуля {t} _c} $$ (5)

где форма матрицы вращения из глобальной системы координат в локальную систему координат и соответствующие углы поворота показаны в Таблице 3

Согласно формулам (1) - (5), факторы Шмида соответствующих систем скольжения при направлениях нагрузки были \ (\ overset {\ rightharpoonup} {f_1} \) и \ (\ overset {\ rightharpoonup} {f_2} \ ) показаны в Таблице 4. (i) Значение c / a для 6H-SiC достигло 4,901, что намного больше 1,633. Следовательно, критическое напряжение сдвига, необходимое для базового скольжения, было ниже, чем для призматической системы скольжения. Когда обработанная поверхность была базовой плоскостью, коэффициент базовой системы скольжения был выше, чем у других систем скольжения. Следовательно, когда режимы обработки были выбраны как \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ ((0001) / \ left [10 \ overline {1 } 0 \ right] \) сначала произошло базальное скольжение . (ii) Когда режимы обработки были выбраны как \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), только с учетом направлений загрузки \ (\ overset {\ rightharpoonup} {f_1} \) и \ ( \ overset {\ rightharpoonup} {f_2} \) теоретически было невозможно, чтобы произошло базальное скольжение, и движение призматического скольжения имело приоритет. (iii) Когда режимы обработки были выбраны как \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) ) / \ left [0001 \ right] \), как показано на рис. 4, наконечник был серьезно изношен на начальном этапе обработки, и \ (\ overset {\ rightharpoonup} {f_2} \) сыграл решающую роль в процесс царапания. Следовательно, движение скольжения будет происходить в призматической системе скольжения, симметрично распределенной с плоскостью YOZ в глобальных координатах.

Распределение поверхностных / подземных повреждений

Как показано на рис. 6a, b, когда \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и \ ((0001) / \ left [01 \ overline {1 } 0 \ right] \), движение скольжения в основном происходило в системе скольжения \ ((0001) / <1 \ overline {2} 10> \), что связано с продвижением инструмента вперед. Соответствующий режим скользящего движения согласуется с результатами расчета коэффициента Шмидта. В приповерхностной области наблюдались нанокристаллические зерна и отклонения решетки, и эти повреждения образовывали зоны неправильной деформации решетки. Аморфная фаза покрывала всю обработанную поверхность, а глубина дислокации была близка к глубине слоя искажения решетки.

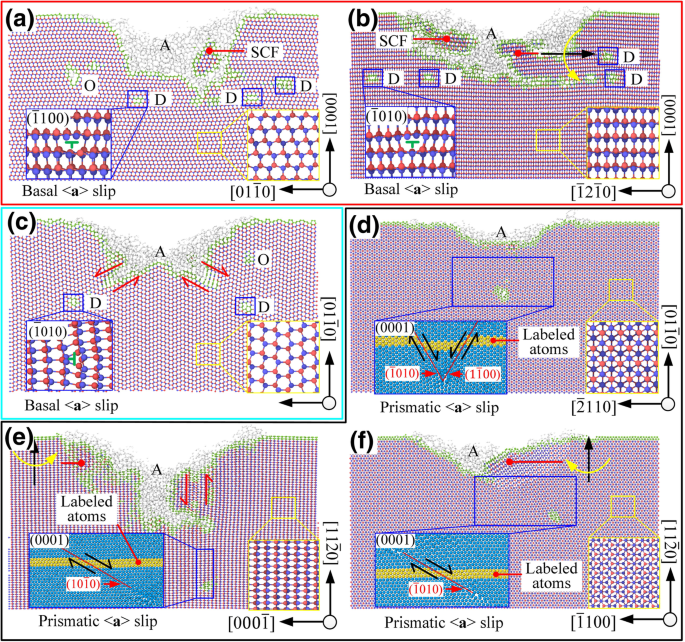
Поперечное сечение обрабатываемой поверхности, D вывих, A аморфная фаза, СКФ монокристаллическая форма, O - дефект другого типа, где a - е - соответствующие режимы процесса \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) и \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) соответственно.

Когда выбрано \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), в качестве коэффициента Шмидта базального < а > скольжение равно 0, базальный < a > Промежуток не должен происходить теоретически. Но угол между направлением нагрузки \ (\ overset {\ rightharpoonup} {f_1} \) и направлением скольжения \ (\ left [11 \ overline {2} 0 \ right] \) составлял всего 5,3 °. Под действием сдвига из-за относительного движения между контактной областью и бесконтактной областью (см. Рис. 6c) базальная < a > проскальзывание было инициировано перед призматическим скольжением в режиме обработки \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) и произошло по обе стороны от V-образной канавки. В режиме обработки \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) углы между направлением нагрузки \ (\ overset {\ rightharpoonup } {f_1} \) и направления скольжения \ (\ left [1 \ overline {2} 10 \ right] \) и \ (\ left [\ overline {1} \ overline {1} 20 \ right] \) были 24,7 ° и 35,3 ° соответственно. Сдвиговое действие не вызывало скользящего движения базовой плоскости. Соответствующий режим движения скольжения согласуется с результатами расчета коэффициента Шмидта. Как показано на рис. 6e, когда была выбрана \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), система скольжения \ (\ left [ 1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) имел высокий коэффициент Шмидта при совместном действии \ (\ overset {\ rightharpoonup} {f_1} \) и \ (\ overset {\ rightharpoonup} {f_2} \), что неизбежно приведет к большой глубине подповерхностного поврежденного слоя. Искажение решетки и аморфная фаза также существовали, но, в отличие от обработки на базисной плоскости, глубина дислокации была значительно больше, чем у искажения решетки. sp ³ → sp ² переходное поведение произошло в подповерхностной области.

Когда направление обработки было параллельно c По оси, из-за сильного износа наконечника, призматическое скольжение, вызванное экструзией вниз, было основным режимом движения скольжения в стабильной стадии царапания. Соответствующий режим движения скольжения соответствовал результатам расчета коэффициента Шмидта. Когда было выбрано \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) с направлением нагрузки \ (\ overset {\ rightharpoonup} {f_2} \), системы скольжения \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) и \ (\ left [\ overline {1} \ overline {1} 20 \ right] / \ left (1 \ overline {1} 00 \ right) \) имел тот же коэффициент Шмидта, поперечное скольжение произошло на двух поверхностях скольжения под углом 60 °, а затем возник эффект закрепления, который препятствовал скольжению. . Таким образом, максимальная глубина подземного повреждения SSD _макс будет меньше или равно h _т загар θ / 2 детская кроватка α / 2, где θ =101 ° - теоретический угол наноканавки, а α =60 ° - угол между плоскостью скольжения \ (\ left (\ overline {1} 010 \ right) \) и \ (\ left (1 \ overline {1}) 00 \ вправо) \). При выборе \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) системы скольжения \ (\ left [\ overline {2} 110 \ right] / \ left ( 0 \ overline {1} 10 \ right) \) и \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) также имели одинаковый коэффициент Шмидта, но на движение скольжения повлиял неравномерный износ наконечника, и возникла только система скольжения \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \).

Таким образом, как показано на рис. 7, повреждения в подповерхностных областях при различных условиях обработки были в основном дислокациями, искажением решетки (кручение / относительное скольжение) и аморфной фазой. Деформация 6H-SiC в основном вызывалась движением скольжения, некристаллизацией материалов и нерегулярным искажением решетки. Основными формами деформации скольжения были базисное скольжение и призматическое скольжение, которые тесно связаны с обрабатываемой поверхностью / направлением.

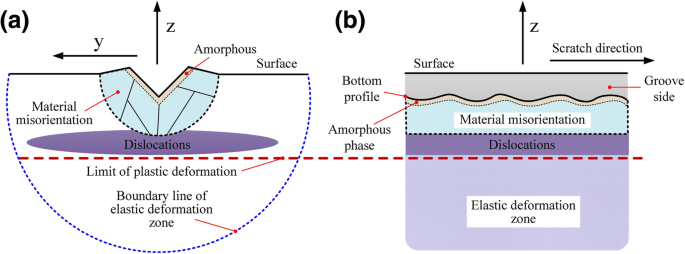
Распределение формы повреждений обработанной поверхности / подповерхности. а xy поперечное сечение. б xz поперечное сечение