Управляемая поляризация долины с использованием дефектов двойной линии силицена из-за спин-орбитальной связи Рашбы

Введение

Силицен, однослойно-сотовая решетка из атомов кремния с низким уровнем выпуклости, является потенциально привлекательной альтернативой графену для приложений долотроники. Низкая деформация структуры приводит к относительно большой спин-орбитальной связи (SOC) в силицене, а значительная энергетическая щель примерно 1,55 мэВ оценивается в точках Дирака K и K ^′ [1] В отличие от графена, соотношение низкоэнергетической дисперсии силицена имеет параболическую, а не линейную форму. Благодаря структуре выпучивания, зонной структурой силицена можно управлять путем приложения электрического поля, и даже может происходить топологический фазовый переход от квантового спинового холловского изолятора к квантовому холловскому диэлектрику долины [2, 3]. Силицен был успешно синтезирован на поверхности таких подложек, как Ag (111), Ir (111) и ZrB2 (0001) [4–6], а его автономная стабильная структура также была предсказана в нескольких теоретических исследованиях [7 ]. Что наиболее важно, силиценовый полевой транзистор (FET), работающий при комнатной температуре, был успешно обнаружен экспериментально [8]. Возможность настройки электрического поля и совместимость с существующими устройствами на основе кремния делают силицен потенциальным двумерным материалом для применения в доллотронике следующего поколения.

В двумерных (2D) материалах, таких как графен и дихалькогениды переходных металлов (MoS ₂ и т. д.), границы зерен между двумя доменами материала с различной кристаллографической ориентацией являются идеальным выбором для достижения поляризации долины и привлекают значительное внимание [9–14]. В последнее время дефекты вытянутой линии (ELD) в силицене были тщательно исследованы в соответствии с расчетами из первых принципов [15, 16], и было обнаружено, что дефект 5-5-8 (далее сокращенно «дефект линии») является определяющим. наиболее стабильная и наиболее легко формируемая структура. Спиновая и долинная поляризация дефекта линии силицена исследованы теоретически [17–19]. Формирование дефекта линии можно представить как сшивание зигзагообразных краев двух зерен Si с помощью адсорбированные атомы Si, где обе стороны дефекта линии демонстрируют поведение, подобное псевдокромке, а границы зигзагообразного края действуют как псевдокреб [16]. Очевидно, такая решетка имеет зеркальную симметрию относительно линии дефект и соответствующие векторы решетки в «левой» и «правой» областях, разделенных дефектом, противоречат друг другу [10, 11]. В таком линейном дефекте с границей области инверсии A / B подрешетки и индексы долин меняются местами при пересечении дефекта. Дефект линии полупрозрачен для квазичастиц в графене, и при большом угле падения возникает высокая поляризация долины. Поляризация долины q _y (групповая скорость электрона по y направление) в зависимости от дефекта линии. Для графена, который имеет линейную дисперсию и постоянную групповую скорость, поляризация долины может достигать около 100% при больших | q _y | (соответствует большому углу падения), а он уменьшается как | q _y | убывает и исчезает как | q _y | ∼0 [9, 14]. Напротив, силицен имеет две разные характеристики пропускания [17, 18]:во-первых, эти две впадины становятся неразличимыми, поскольку энергия Ферми близка к краю зоны из-за параболического дисперсионного соотношения, а во-вторых, пропускание ограничено из-за спирального краевое состояние, протекающее обратно пропорционально по обе стороны от линейного дефекта, как показано на рис. 1c. Естественно, система с SOC в конкретном RSOC является многообещающим кандидатом для эффективного спинового полевого транзистора. RSOC генерирует эффективное магнитное поле в плоскости и вызывает прецессию спина, которая вводится перпендикулярно плоскости удержания. Спиновая поляризация [20] и инверсия [21] были исследованы в закрытых силиценовых нанолентах. Теоретические расчеты показали, что энергетическая зона силицена может существенно модулироваться RSOC [22, 23]. Например, при относительно высоком RSOC полоса спада (вверх) на уровне K ( К ^′ ) долина сдвигается вверх, в то время как остальные спиновые зоны в зоне проводимости остаются неизменными. Принимая во внимание особенности передачи в дефекте линии силицена и влияние RSOC в силицене, практические полностью электрические схемы для генерации долинно-поляризованных носителей становятся возможными.

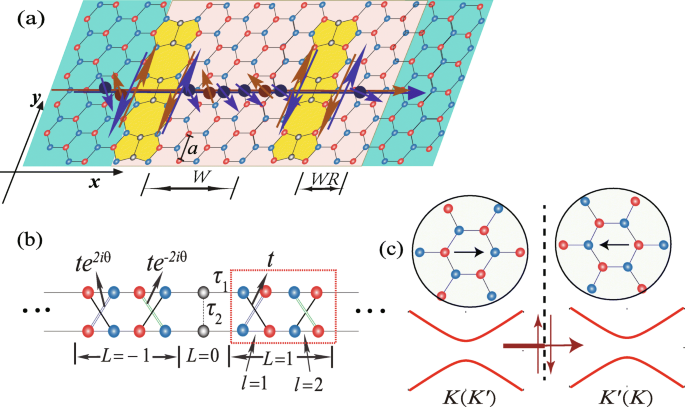
а Принципиальная схема процесса прецессии состояний ( K , ↑ ) (красная сфера) и ( K ^′ , ↓ ) (синяя сфера) через лист силицена с двумя параллельными линейными дефектами, где синий (красный) кружок обозначает A ( B ) подрешетка. Состояния ( K , ↑ ) и ( K ^′ , ↓ ) циркулируют вдоль псевдо-края, и предполагается, что RSOC, а также электрическое поле существуют во французской серой области. Вт ( W =2) и WR ( WR =1) представляют ширину области рассеяния в единицах \ (\ sqrt {3} a \). б Упрощенная модель решетки бесконечного силицена с линейным дефектом, где θ = k _y а а пунктирный прямоугольник соответствует суперячейке. В элементарной ячейке точки решетки задаются набором индексов ( L, l ). c Передача для одного спинового состояния в K ( К ^′ ) долина поперек линейного дефекта с инверсионными доменными границами. На вставках показана ориентация кристаллической решетки в двух доменах, разделенных дефектом линии (пунктирная линия). Толстые / тонкие линии указывают на то, что передача ограничена через дефект линии из-за спиральных краевых состояний, протекающих в обратном направлении вдоль псевдоребра

В этой статье мы предлагаем эффективный способ поляризации фермионов Дирака различных долин с использованием дефектов двойной линии силицена, создавая таким образом отчетливую поляризацию долин с помощью электрического поля в силицене. Наши результаты показывают, что, когда энергия Ферми находится вблизи дна зоны проводимости, колебательные изображения коэффициентов пропускания из двух долин, которые содержат широкие осциллирующие пики и надиры, совпадают до тех пор, пока RSOC превышает собственное SOC, в то время как присутствие только одиночный дефект линии не может разогнать долинно-зависимые электроны. Когда задействованы два параллельных линейных дефекта, колеблющиеся надиры превращаются в плато с нулевым пропусканием, и эффективная модуляция долинно-зависимого переноса может быть реализована путем изменения периодичности колебаний двух долин Дирака с помощью перпендикулярного электрического поля, где периодичность колебаний равна две впадины увеличиваются и уменьшаются, что приводит к идеальной поляризации долин в соответствующих областях с широким плато пик-ноль. В эксперименте можно обнаружить такой чистый ток долины, измерив изменение проводимости с электрическим полем. Это явление обеспечивает другой путь для эффективной модуляции поляризации впадины в силиценовых устройствах за счет использования RSOC и электрических полей.

Методы

Давайте начнем со схемы устройства с двухконтактным дефектом линии силицена, как показано на рис. 1а, на котором прецессия спина проиллюстрирована для генерации тока поляризованной долины из-за RSOC и электрического поля. Предполагается, что RSOC существует на одной стороне дефекта линии шириной W . и WR в единицах \ (\ sqrt {3} a \), где a =3,86 Å - постоянная решетки чистого силицена, как показано на рис. 1а. Когда энергия Ферми находится у дна зоны проводимости, состояния ( K , ↓ ) [( К , ↓ ) соответствует состоянию в долине K с ↓ (вниз) вращение] и ( K ^′ , ↑ ) находятся в промежутке из-за манипуляции энергетической полосой от RSOC. Два других состояния ( K , ↑ ) и ( K ^′ , ↓ ), циркулируют по псевдокромке из-за характеристики синхронизации спинового импульса от SOC [24], как показано на рис. 1a. Для определенного состояния спина он течет по псевдокромке с противоположными направлениями по обе стороны от линейного дефекта, который может действовать как фильтр и ограничивать передачу через линейный дефект, как показано на рис. 1c.

Модель решетки в представлении сильной привязки используется для описания системы линейных дефектов с RSOC как [17, 22]

где \ (c_ {i \ alpha} ^ {\ dag} \) и \ (c_ {i_ {y} \ alpha, \ gamma / \ delta} ^ {\ dag} \) представляют оператор рождения электрона со спином α на сайте силицена i и дефект линии, соответственно, и 〈〉 / 〈〈 〉〉 пробегает все узлы перескока между ближайшими / следующими ближайшими соседями. Первые три члена обозначают переключение между ближайшими соседями, а параметры t , τ ₁ , и τ ₂ обозначают различные энергии прыжка ближайших соседей в модели сильной связи, как показано на рис. 1b. Четвертый член - это эффективный SOC с параметром скачкообразного изменения t _так , и ν _ij =± 1 для перескока против часовой стрелки (по часовой стрелке) между следующими ближайшими-соседними узлами относительно положительного z -ось. Теоретическое исследование [16] показало, что два ближайших атома Si в дефектной области относительно идентичны атомам в исходной области и что все атомы Si остаются в sp ² - sp ³ гибридизированное состояние. Поэтому разумно установить τ ₂ = τ ₁ = t . В пятом члене Δ _z - потенциал подрешетки в шахматном порядке, возникающий из-за электрического поля, перпендикулярного листу силицена, и μ _я =± 1 для A ( B ) сайт. Последний член представляет собой внешний термин RSOC, где t _R - параметр перескока по спин-орбите Рашбы. г _ij это единичный вектор, указывающий с сайта j к я , и \ (\ vec {\ sigma} =(\ sigma ^ {x}, \ sigma ^ {y}, \ sigma ^ {z}) \) в уравнении. 1 - вектор вещественных спиновых матриц Паули. RSOC возникает из-за внешнего потенциала, приложенного либо электрическим затвором, либо адсорбцией атомов металла, либо подложками [20, 25], которые могут резко нарушить симметрию инверсии структуры силицена. Примечательно, что внешний RSOC, возникающий из-за электрического поля, игнорируется, потому что он очень слаб.

Значения ELD силицена показаны на рис. 1a, который сильно простирается вдоль y направление. Трансляционная симметрия структуры решетки вдоль y direction указывает, что k _y является сохраняющейся величиной и что операторы создания (уничтожения) могут быть переписаны следующим образом в соответствии с преобразованием Фурье (спин-индекс игнорируется) [17]:

Тогда матрица гамильтониана в уравнении. 1 разделяется на \ (H =\ sum _ {k_ {y}} H_ {k_ {y}} \), где \ (H_ {k_ {y}} \) можно описать в следующем виде:

где \ (\ varphi _ {i, l} ^ {\ dag} =\ left [c _ {{{k} _ {y}}, i, l, A \ uparrow} ^ {\ dag}, c _ {{{ k} _ {y}}, i, l, A \ downarrow} ^ {\ dag}, c _ {{k} _ {y}}, i, l, B \ uparrow} ^ {\ dag}, c_ { {{k} _ {y}}, i, l, B \ downarrow} ^ {\ dag} \ right] \), i в наборе index ( i, l ) представляет положение суперячейки \ ((\ bar {i} =- i) \), а l =1 или 2 обозначают различные зигзагообразные цепочки в суперячейке, как показано в пунктирном прямоугольнике на рис. 1b. \ (\ hat {T_ {ll '}} \) представляет гамильтонову матрицу каждой зигзагообразной цепочки ( l = l ^′ ) в суперячейке или взаимодействие между различными зигзагообразными цепочками ( l ≠ l ^′ ).

Отмечается, что две долины K и K ^′ теперь приводятся к [0, ± π / 3 а ] из-за вставки дефекта линии. Матрица передачи η ( η = К / К ^′ ) долина рассчитывается по обобщенной формуле Ландауэра [26, 27],

где

и

Здесь \ (- Im \ Sigma _ {L, R} =- \ left (\ Sigma _ {L, R} ^ {r} - \ Sigma _ {L, R} ^ {a} \ right) / 2i \ ) - положительные полуопределенные матрицы с четко определенным квадратным корнем из матрицы, где \ (\ Sigma _ {L, R} ^ {a} =\ left [\ Sigma _ {L, R} ^ {r} \ right] ^ { \ dag} \) - это замедленная / повышенная собственная энергия левого / правого отведения. Подматрица 16 × 16 G ^г - запаздывающая функция Грина, которая соединяет первую и последнюю суперячейки вдоль x направление и может быть вычислено с использованием метода рекурсивной функции Грина. Суммарные коэффициенты передачи η долина - это \ (T _ {\ eta} =T ^ {\ uparrow \ uparrow} _ {\ eta} + T ^ {\ uparrow \ downarrow} _ {\ eta} + T ^ {\ downarrow \ uparrow} _ {\ eta } + T ^ {\ downarrow \ downarrow} _ {\ eta} \), а спиновая поляризация P _s и поляризация долины P _η может быть выдан

Результаты и обсуждение

При расчетах коэффициентов передачи, зависящих от спина, мы полагаем τ ₂ = τ ₁ = t =1 в качестве единицы энергии, сила SOC t _так =0,005 t , а энергия Ферми E _f =1,001 t _так , который расположен в нижней части зоны проводимости. Ширина области рассеяния составляет W . =1000 для однолинейного дефекта и дополнительная ширина WR =1000 также учитывается для двух параллельных линейных дефектов, как показано на рис. 1а.

На рисунке 2 показаны коэффициенты передачи с сохранением спина / переворота спина долины \ (\ eta, T ^ {sc} _ {\ eta} / T ^ {sf} _ {\ eta} \) в зависимости от инцидента. углы α (a) и численности RSOC t _R (б – г). Рисунки 2a – c соответствуют случаю одиночного линейного дефекта, а (d) - случаю двух параллельных линейных дефектов. Показано, что при определенном t _R (например, t _R =5 t _так как на рис. 2a), зависящие от спина коэффициенты передачи \ (T ^ {sc} _ {K} / T ^ {sf} _ {K} \) постоянны и не зависят от углов падения из-за параболического дисперсионного соотношения , как показано на рис. 2а. Следовательно, в следующих расчетах мы можем использовать угол падения α =0 в качестве примера. Для слабого t _R осциллирующее явление, подобное тому, что происходит в двумерном электронном газе [26, 27], возникает из-за расщепления Рашбы, как показано на вставке к рис. 2б. Как t _R увеличивается ( t _R > т _так ), \ (T_ {K} ^ {\ uparrow \ uparrow} \) и \ (T_ {K} ^ {\ uparrow \ downarrow} \) имеют ту же периодичность колебаний и почти такие же величины, что и t _R который состоит из некоторых пиков и надиров колебаний, а \ (T_ {K} ^ {\ downarrow \ downarrow} / T_ {K} ^ {\ downarrow \ uparrow} \) стремится к нулю, поскольку энергия Ферми находится в его щели, так как показано на рис. 2б. Таким образом, общий коэффициент передачи K Долина в основном обусловлена ​​государством раскрутки. Фактически, колебательные изображения двух долин, K и K ^′ , совпадают, а коэффициенты передачи K ^′ долину в основном вносят электроны со спином вниз.

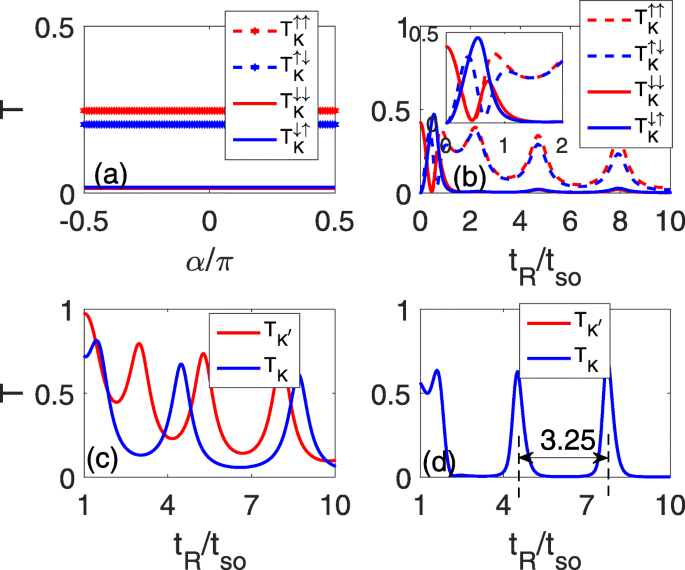
Коэффициенты передачи с сохранением спина и переворотом спина в зависимости от углов падения α в t _R =5 t _так через а и как функции силы RSOC t _R в б - г , где a - c предназначены для дефекта одной строки и d для двух параллельных линейных дефектов, с Δ _z =0,2 t _так в c

В присутствии перпендикулярного электрического поля вырождение долины снимается, и колебательное поведение двух долин различается:периодичность колебаний K долина увеличивается, а у K ^′ долина уменьшается, как показано на рис. 2в. Однако кажется невозможным отфильтровать одно состояние конической долины с помощью только одного дефекта линии, потому что колеблющиеся надиры имеют определенную величину. Естественно, можно рассмотреть явление колебания с двумя параллельными линейными дефектами, чтобы еще больше ограничить передачу, как показано на рис. 2d. Сравнение рис. 2b с d показывает, что пик колебаний становится узким и острым, в то время как надир колебаний расширяется и ослабевает, что формирует платформу с нулевым пропусканием. Расстояние между двумя соседними пиками колебаний зафиксировано на 3,25 t _так , как показано двумя пунктирными линиями на рис. 2d.

Чтобы добиться лучшего эффекта фильтра впадины, мы концентрируем наше внимание на эффекте перпендикулярного электрического поля. Результаты этого эффекта показаны на рис. 3. Как обсуждалось выше, периодичность колебаний двух долин изменяется противоположным образом, и исходные перекрывающиеся пики колебаний на рис. 2d уменьшаются. Между тем, плато с нулевым пропусканием расширяется и сужается для T _К и \ (T_ {K ^ {\ prime}} \) соответственно, как показано на рис. 3a и b. В Δ _z =0,15 t _так , пространство между двумя соседними пиками колебаний превращается в 3,6 t _так для T _К , при этом снижается до 3,1 t _так для \ (T_ {K ^ {\ prime}}} \), как показано двумя синими и красными пунктирными линиями, показанными на рис. 3a. По мере усиления электрического поля пространство между двумя соседними пиками колебаний продолжает увеличиваться / уменьшаться в течение T _К / \ (T_ {K ^ {\ prime}} \), что составляет 5,4 t _так /2.8t _так в Δ _z =0,3 t _так , как показано на рис. 3b. Изменение периодичности колебаний приведет к соответствующим областям широкого плато пик-ноль, где идеальная поляризация впадины с P _η =± 1 плато может быть реализовано, как показано на рис. 3c и d. Одновременно показано, что высокоспиновая поляризация P _s также возникает, когда P _η =± 1.

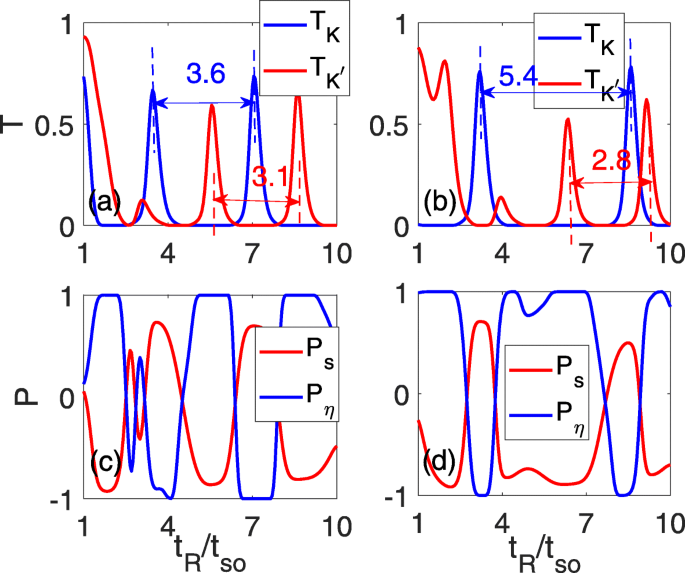
Суммарные коэффициенты передачи \ (T_ {K} / T_ {K ^ {\ prime}} \) ( a , b ) и поляризация спин / долина ( c , d ) как функция силы RSOC t _R для разных подрешеточных потенциалов. Δ _z =0,15 t _так через а и c и Δ _z =0,3 t _так в б и d ; остальные параметры идентичны показанным на рис. 2d

Однако из-за неконтролируемости RSOC все еще трудно экспериментально обнаружить такие чистые токи впадины, даже несмотря на то, что RSOC, индуцированный в дефекте линии, может быть больше, чем собственное SOC. Чтобы удобно исследовать чистый ток долины экспериментально, мы также исследуем коэффициенты пропускания и поляризацию долины как функцию электрического поля, которым можно непрерывно управлять во время эксперимента. Показано, что идеальная поляризация долины с P _η =± 1 может появиться в определенном диапазоне Δ _z и что он может измениться с P _η =От 1 до P _η =−1 при увеличении электрического поля, как показано на рис. 4a. Для определенного t _R (например, t _R =7,2 t _так , как показано пунктирной линией на рис. 4a), коэффициенты передачи \ (T_ {K} / T_ {K ^ {\ prime}} \) колеблются с Δ _z , где широкие пики пропускания K ( К ^′ ) долины соответствуют плато нулевого пропускания K ^′ ( К ) Долина. Общие коэффициенты передачи в основном вносятся одной долиной при изменении электрического поля, и идеальная поляризация впадины всегда может иметь место около максимального значения \ (T_ {K} / T_ {K ^ {\ prime}} \), как показано на Рис. 4б. Поскольку энергия Ферми уходит от края зоны, идеальная поляризация долины может выжить даже при E _f =1,5 t _так , где соотношение плато может сохраняться, как показано на рис. 4c. Во время эксперимента можно анализировать электрические токи с долинной поляризацией от левого провода к правому с помощью экспериментально измеряемой величины, такой как проводимость, которая пропорциональна общему коэффициенту передачи. Максимальная проводимость между двумя минимальными значениями (иногда они равны нулю) должна быть из одной впадины. Мы можем оценить величину проводимости по формуле \ (G =\ frac {e ^ {2}} {h} \ int _ {- k_ {F}} ^ {k_ {F}} T \ frac {dk_ {y}} {2 \ pi / L_ {y}} =\ frac {e ^ {2}} {h} \ frac {Ly \ sqrt {E ^ {2} -t ^ {2} _ {so}} } {2 \ pi \ hbar v_ {F}} 2T \) [28], где L _y =2 а ≈7,72Å - ширина дефекта линии силицена, v _F =5,5 × 10 ⁵ м / s - скорость Ферми, \ (\ hbar =h / 2 \ pi \) - приведенная постоянная Планка с \ (\ phantom {\ dot {i} \!} h =4.13566743 \ times 10 ^ {- 15} эВ \ cdot s, T =T_ {K} + T_ {K '} \) - общий коэффициент передачи, а E - локальная энергия падающих электронов. Тогда проводимость будет примерно \ (G \ приблизительно \ left [0,7T \ sqrt {E ^ {2} -t ^ {2} _ {so}} / эВ \ right] \ frac {e ^ {2}} { час}\). Также обнаружено, что по мере того, как локальная энергия на стороне падения повышается до E =0,15 t ( т =1,6 эВ ), коэффициенты пропускания двух впадин изменяются лишь незначительно по сравнению с рис. 4c из-за сохранения спина и импульса, а соотношение пик пропускания и нулевого плато сохраняется, как показано на рис. 4d. В этом случае проводимость составляет примерно \ (G \ приблизительно 0,17 Тл \ frac {e ^ {2}} {h} \), что является значительным и может быть обнаружено экспериментально. Энергетическое окно для наблюдения этого явления составляет около 0,5 t _так ( т _так < E <1,5 т _так ), который пропорционален t _так . В эксперименте нетрудно контролировать энергию Ферми вблизи края зоны, и щель SOC может быть даже радикально увеличена до 44 мэВ за счет близости к бислою Bi (111) [29], что может значительно улучшить область энергий для обнаружения чистого долинное течение. Более того, вычислительная модель также может быть применима к другим аналогам графена, германена [30], станена и MoS ₂ с низкой изгибом. [31–36], которые имеют еще большую ширину запрещенной зоны [37, 38], а также сильные SOC (сила SOC может достигать 0,1 эВ для станена [38, 39]). В реальном эксперименте легко реализовать сильное RSOC, которое может превышать собственное SOC, нарушая симметрию зеркала в плоскости со специальной подложкой [40]. Следовательно, эта схема может быть полностью осуществима в эксперименте.

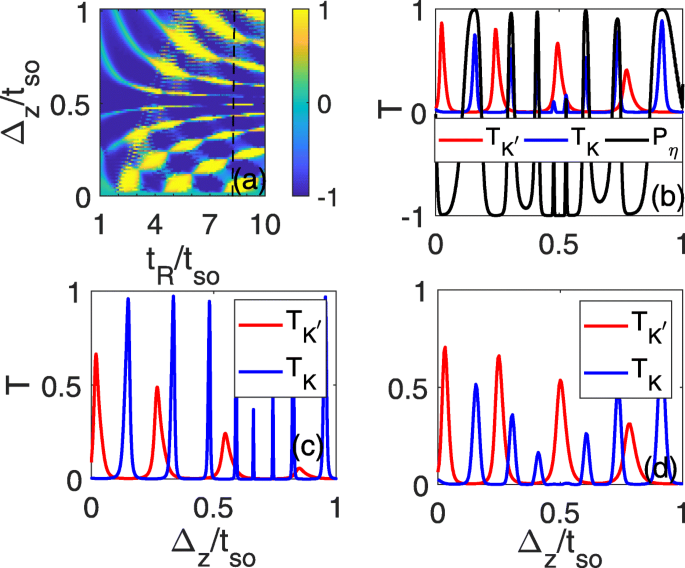
Поляризация долины a и \ (T_ {K} / T_ {K ^ {\ prime}} \) ( b - г ) как функции от Δ _z и t _R . т _R =7,2 t _так в ( b - г ), E _f =1,5 t _так в c и d , а энергия на месте составляет E =0,15 t в левом электроде в d ; все остальные параметры идентичны показанным на рис. 2d