Теоретическая система трибоэлектрических наногенераторов контактного режима для повышения эффективности преобразования энергии

Фон

Искусственный интеллект и облачная сеть постепенно улучшают качество нашей современной жизни с быстрым развитием электроники следующего поколения для умного дома, мониторинга здоровья, развлечений и мониторинга окружающей среды [1,2,3]. Питание такого большого количества электроники стало невыполнимой задачей с использованием существующих технологий аккумуляторов, учитывая их большой размер, короткий срок службы и особенно проблемы с быстрой зарядкой. Это стало одним из важнейших препятствий для разработки экологически безопасных источников питания, подходящих для носимой электроники [4,5,6].

В настоящее время трибоэлектрические наногенераторы (ТЭНГ) на основе трибоэлектрификации продемонстрировали привлекательную технологию сбора механической энергии. Это многообещающий кандидат для носимой электроники благодаря своим многочисленным преимуществам, включая гибкость [7], экономичность [8], простой процесс изготовления [9], защиту окружающей среды [10] и универсальность [11]. Он широко используется для получения энергии из окружающей механической энергии. Кроме того, его можно использовать для интеграции с носимым устройством для приложений с автономным питанием [12,13,14]. На данный момент используется множество методов для увеличения мощности, включая морфологию поверхности [15, 16], оптимизацию материала [17, 18], инжекцию заряда [19, 20], оптимизацию структуры [21, 22] и мульти-наногенераторы. [23, 24]. Несмотря на быстрое улучшение выходной производительности, окончательная модель для анализа эффективности преобразования энергии отсутствует. Был опубликован ряд теоретических объяснений для различных режимов TENG [25,26,27]. Однако в большинстве анализов не обсуждается весь процесс преобразования энергии, а уделяется внимание только выходной мощности. Что еще более важно, более высокая выходная мощность не означает более высокую эффективность преобразования энергии и может даже оказаться контрпродуктивной. Это несколько затруднило разработку более эффективных TENG из-за отсутствия прямых исследований эффективности преобразования энергии.

В данной работе мы систематически и непосредственно анализировали мощность и эффективность преобразования контактных ТЭНов с учетом всего процесса. Во-первых, выходя за рамки обычного анализа, была введена сжимающая сила для получения более универсального профиля движения, что обеспечило лучшее понимание принципа работы процесса разъединения контактов. Затем, согласно уравнениям движения, были представлены явные уравнения для важных характеристик устройства во всем процессе контакта и разъединения. Наконец, систематически исследовалось влияние свойств материала, структурных параметров и экспериментального фактора на максимальную мощность и особенно эффективность преобразования энергии. Мы можем получить максимальный КПД и мощность, рационально рассчитав параметры, особенно сжимающую силу. Это реалистично и полезно для более эффективных ТЭНов. Важно отметить, что у него есть хорошие шансы установить стандарты для количественной оценки эффективности TENG, которые закладывают основу для дальнейшей индустриализации и многофункциональности TENG.

Методы

Основной принцип работы ТЭНов основан на трибоэлектрификации и электростатической индукции. По фрикционным материалам его можно приблизительно разделить на два типа. Из-за работы выхода и трения диэлектрический материал и материал проводника выбраны в качестве трибоэлектрических пар. Как показано на рис. 1, верхний слой состоит из верхнего электрода (TE), а диэлектрический слой может перемещаться вверх и вниз, тогда как нижний электрод (BE) закреплен на подложке. Два слоя соединены нагрузочным резистором R . . Отрыв и контактный процесс показаны на рис. 1а, б соответственно. В процессе разделения электроны текут в BE из TE и возвращаются в TE в процессе контакта.

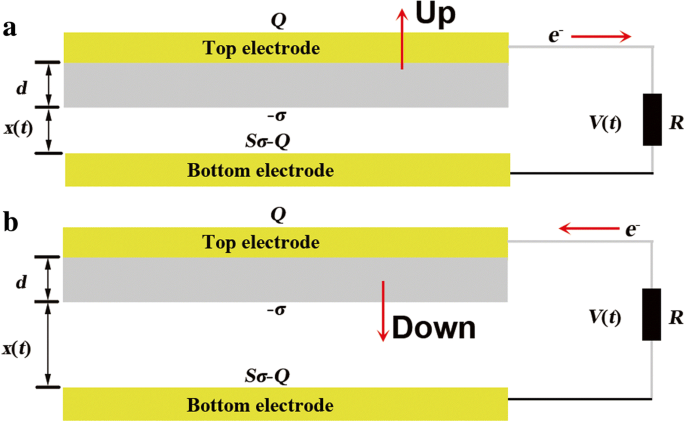
Теоретическая модель контактного режима TENGA. а Процесс разделения и б контактный процесс

Под действием приложенной силы F , верхний слой будет полностью соприкасаться с нижним слоем. БЭ будет иметь положительный трибоэлектрический заряд с поверхностной плотностью заряда σ а диэлектрический слой имеет такие же заряды с противоположным знаком. В процессе разделения верхний слой отделяется от нижнего на расстояние x ( т ). Это приведет к разности потенциалов V ( т ) между TE и BE из-за электрического поля. Для смещения V ( т ), электроны будут течь между двумя электродами через R . Таким образом, стоимость TE составляет Q . в то время как BE остается с Sσ - В . Напряженность электрического поля в двух областях определяется следующим образом согласно теореме Гаусса.

Внутри диэлектрического слоя:

Внутри воздушного зазора:

где ε ₀ и ε _r - диэлектрическая проницаемость вакуума и относительная диэлектрическая проницаемость соответственно.

V ( т ) должен удовлетворять следующему уравнению:

Согласно закону Ома V ( т ) задается как

Объединяя уравнения, мы можем получить

Уравнение. (5) является основным уравнением TENG. Его можно применить ко всему процессу разделения и контакта. Очевидно, что x ( т ) является одним из важнейших факторов TENG. В отличие от предыдущей работы, мы строим практическое уравнение движения, а не предполагаем его напрямую. В этой статье уравнение движения для всего процесса построено на основе сжимающей силы и экспериментальных условий.

Результаты и обсуждение

Система без пружин

Во-первых, мы рассматриваем только постоянную сжимающую силу F и плотность верхнего слоя. Уравнение движения может быть получено следующим образом (см. Дополнительный файл 1:Примечание 1 и рисунок S1 в ESM). На самом деле x ( т ) всегда имеет максимальное значение x _макс и минимальный ноль. Таким образом, уравнения движения задаются

Уравнения. (6.1) и (6.2) представляют собой процесс разделения и контактный процесс соответственно.

Тогда мы сможем получить переведенную плату. (Подробный вывод находится в Дополнительном файле 1:Примечание 2 в ESM).

В процессе разделения:

где \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F- mg \ right)} \) и Q ₀ = Q ( т ₀ ) в уравнении. (7.1).

В процессе связи:

где \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F + mg \ right)} \), Q ₀ можно рассчитать, присвоив t = t ₀ в уравнение. (8.1).

Следовательно, выходной ток можно получить как I ( т ) = dQ / dt и V ( т ) = RI ( т ).

В зависимости от конкретных параметров, представленных в таблице 1, мы можем получить результаты численных расчетов.

Отношения характеристики-время при разных R весь процесс показан на рис. 2. Зависимости перенесенных зарядов, выходного тока и выходного напряжения при различных нагрузках в процессе контакта показаны на рис. 2a, c, e. Поведение аналогично предыдущим исследованиям [25]. Но процесс разделения изучается редко. Предположим, что поверхностные заряды полностью передаются ТЭ в процессе разделения через долгое время. Как показано на рис. 2b, в состоянии короткого замыкания (SC) заряды в TE могут полностью течь обратно в BE, когда верхний слой прекращает движение ( t =2 мс). Плата не может снизиться до нуля в t =2 мс при R больше 1 МОм. Принимая во внимание, что почти все расходы переводятся на BE, когда R меньше 10 МОм в процессе разделения. Передаваемые заряды в процессе контакта намного меньше, чем в процессе разделения. Этому способствует относительно небольшая движущая сила в процессе раннего контакта. Зависимость выходной ток от времени показана на рис. 2d. В состоянии SC пиковый ток почти такой же, как и в процессе разделения. Когда R больше, кривая текущего времени имеет два локальных максимальных значения, которые находятся в начале и в конце движения. А абсолютный максимальный ток резко падает с увеличением сопротивления. Два локальных максимума в начале и в конце движения обусловлены адекватными электронами и высокоскоростным движением соответственно. Выходное напряжение имеет тот же профиль, что и ток, но другую тенденцию по величине, как показано на рис. 2f (подробное соотношение в ESM см. В дополнительном файле 1:рис. S2). Следует отметить, что абсолютное максимальное значение напряжения намного меньше, чем в процессе разделения. Очевидно, что напряжение и ток не являются симметричными в процессе разделения и контакта. При объединении процесса разделения и контакта выходное напряжение и ток являются переменными.

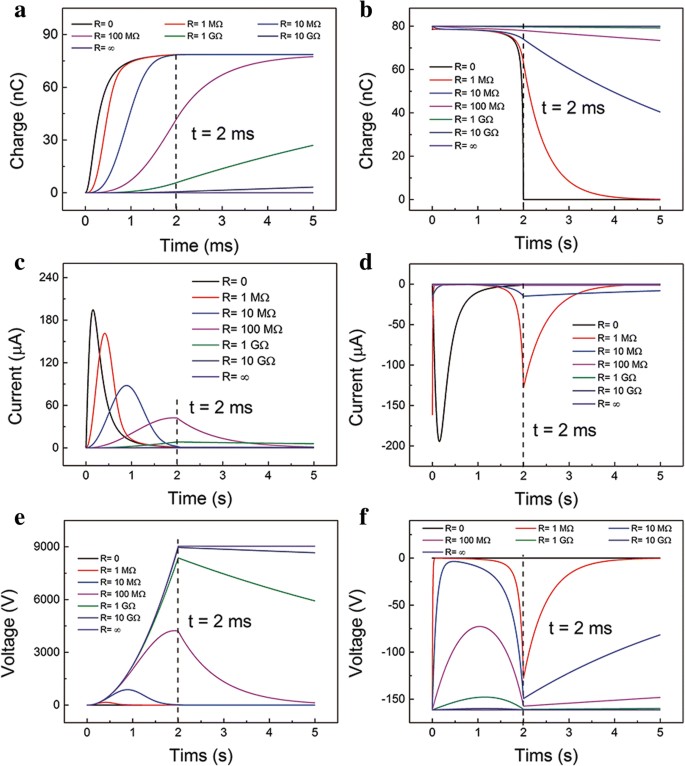
Расчетные выходные характеристики, когда на устройство действует постоянная сжимающая сила F. Отношение перенесенных сборов к времени при разных R в a контактный процесс и б процесс разделения. Текущие отношения при разных R в c контактный процесс и d процесс разделения. Отношение напряжение-время при разных R в е контактный процесс и е процесс разделения

Кроме того, влияние различных параметров на соотношение максимальной мощности P _макс и соответствующее сопротивление показаны на рис. 3. Эти различные параметры можно разделить на материал, структуру и условия эксперимента. Например, параметры материала включают σ и ε _r . Структурными параметрами в основном являются размер области S, x _макс и г. Сжимающая сила F параметр эксперимента. Видно, что σ, S , F , и x _макс сильно влияют на P _макс , как показано на рис. 3a – d. P _макс резко возрастает как σ, S , F , и x _макс увеличивать. Параметр σ и S в основном решают сумму сборов, которые могут быть переведены. Параметры F и x _макс в основном влияют на уравнения движения. Соответствующее оптимальное сопротивление уменьшается с x _макс уменьшается, хотя на него редко влияет σ, S , и F. Кроме того, параметры d и ε _r редко влияют на P _макс и соответствующее сопротивление, как показано на рис. 3e, f. Это эффективная толщина диэлектрического слоя d ₀ = d / ε _r что мало влияет на работу TENG. Мы можем настроить эти параметры, чтобы контролировать максимальную мощность. Стоит отметить, что соответствующее сопротивление обычно является сопротивлением нагрузки электроники.

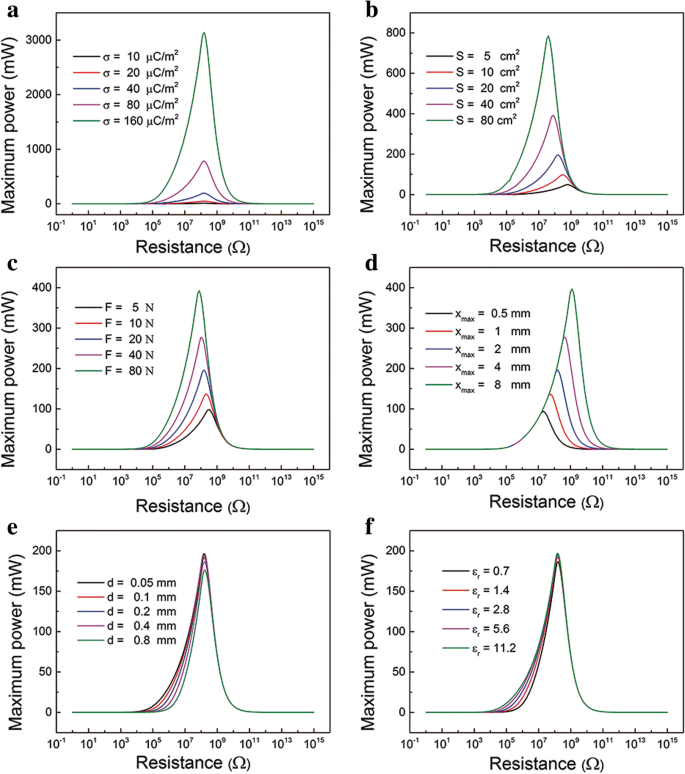
Влияние параметров на P _макс и соответствующее сопротивление. Профиль мгновенной мощности с R в разные а плотность поверхностного заряда σ, b размер области S , c сжимающая сила F , d максимальное разделительное расстояние x _макс , e толщина диэлектрического слоя d , и f ε _r

Система Spring

Для более популярных условий эксперимента в комплект входит пружинная система. Сжимающая сила F применяется периодически, как показано на рис. 4а. В процессе разделения ( T = t ₁ ), есть только восстанавливающая сила пружины и силы тяжести, поэтому F =0. В процессе связи ( T = t ₂ + t ₃ ) сжимающая сила F добавлен. И это будет продолжаться еще долго после того, как два слоя полностью соприкоснутся. Кривые движения показаны на рис. 4б. Расчетные уравнения движения и выходные характеристики выводятся следующим образом. (Дополнительный файл 1:Примечание 3 в ESM)

где \ ({\ omega} _0 ^ 2 =k / m \). И уравнения. (9.1) и (9.2) представляют собой процесс разделения и контактный процесс соответственно.

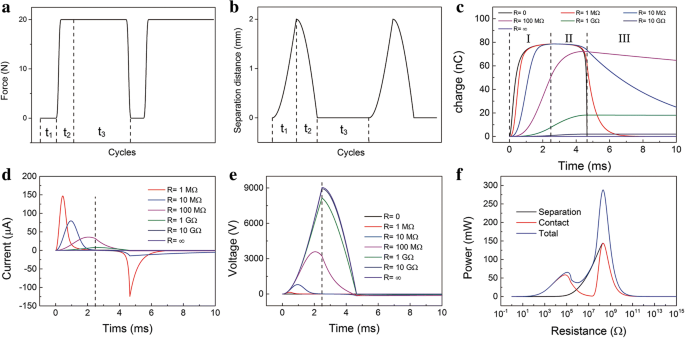
Расчетные характеристики контактно-разделительного режима ТЭНов . а Периодическая сила F . б Периодическое движение верхнего слоя. c Отношение перенесенных сборов к времени при разных R в процессе контакта и разъединения. г Текущие отношения при разных R в процессе контакта и разъединения. е Отношение напряжение-время при разных R в процессе контакта и разъединения. е Связь мгновенной максимальной мощности с сопротивлениями в контакте, разделении и во всем процессе

В процессе разделения:

В процессе связи:

где q ₀ - это сборы, которые передаются от BE к TE в процессе разделения.

Выходной ток и напряжение можно рассчитать как I ( т ) = dQ / dt и V ( т ) = RI ( т ).

Отношение перенесенных сборов к времени при разных R в полном объеме показан на рис. 4в. Процесс передачи заряда разделен на три области, что соответствует периодической силе. Область I представляет собой процесс разделения, а контактный процесс включает области II и III. В регионе I сборы передаются в TE из BE. Сборы в ТЕ продолжают расти. В области II направление потока заряда связано с сопротивлением. Заряды в TE продолжают увеличиваться, когда сопротивление велико ( R ≥ 1 ГОм). Он увеличивается до максимума, затем уменьшается при низком сопротивлении ( R ≤ 100 МОм). Особенно, когда R =0, заряды продолжат убывать в области II. В области III заряды в ТЕ продолжают уменьшаться. Соответствующий выходной ток во всем процессе показан на рис. 4d. Ток в процессе разъединения и контакта имеет обратный знак. Обычно максимальное значение тока в процессе разделения немного больше, чем в процессе контакта. Интересно, что в процессе контакта абсолютное максимальное значение тока появляется в начале процесса контакта или в момент, когда они только что контактируют. Когда сопротивление велико, оно появляется в начале процесса контакта, наоборот. Выходное напряжение увеличивается со временем, а затем уменьшается, как показано на рис. 4e. Выходное напряжение будет отображаться как отрицательное значение в процессе контакта. И абсолютная величина намного меньше, чем в процессе разделения. Эти цифры согласуются с измеренными экспериментальными графиками в литературе. Очевидно, что измеренный выходной ток является переменным, а измеренное выходное напряжение обычно имеет резкий пик. Зависимости мгновенной максимальной мощности от сопротивлений в контакте, разделении и во всем процессе показаны на рис. 4f. ТЭНы достигают своей абсолютной максимальной мгновенной мощности около 200 МОм в процессе разделения и контакта. В процессе контакта он имеет дополнительное локальное максимальное значение около 0,1 МОм. Таким образом, в течение всего процесса мгновенная мощность достигает максимального значения около 200 МОм. Можно видеть, что кривая мощности процесса контакта перекрывается с кривой процесса разделения, когда сопротивление велико. Поскольку максимальное значение тока появляется на пересечении двух процессов, когда R ≥ 200 МОм.

Более того, рассчитанные результаты P _макс и соответствующее оптимальное сопротивление показаны на рис. 5. Как показано на рис. 5a – c, максимальная мгновенная мощность увеличивается с увеличением параметров x _макс , S , и k увеличивать. Это может быть связано с более высокой скоростью передачи электронов. При этом изменяется и соответствующее оптимальное сопротивление. Оптимальное сопротивление уменьшается с S и k возрастает, но имеет обратную тенденцию с x _макс . Влияние параметров σ на P _макс оптимальное сопротивление показано на рис. 5d. P _макс быстро увеличивается с увеличением σ, в то время как оптимальное сопротивление остается постоянным. На оптимальное сопротивление также не влияет ε . _r . Но поскольку ε _r увеличивается, максимальная мгновенная мощность увеличивается, а затем становится насыщенной. F практически не влияет на максимальную мгновенную мощность и оптимальное сопротивление. Во всем процессе контакта и разделения F влияет только на процесс контакта. Таким образом, максимальный ток в процессе разделения остается неизменным. Как показано на рис. 5f, максимальная мгновенная мощность не изменяется. Это отличается от беспружинной системы. В системе без пружины F напрямую влияет на процесс разделения, тем самым влияет на максимальную мощность.

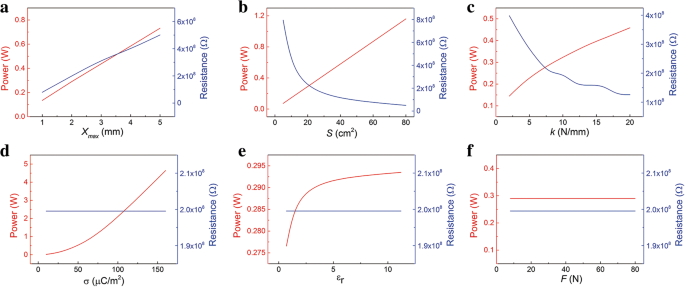
Влияние параметров на P _макс и соответствующее сопротивление в одном цикле. Отношения P _макс и соответствующее сопротивление с параметрами a x _макс , b S , c к , d σ, e ε _r , и f F

Одним словом, P _макс можно увеличить, увеличив максимальное разделительное расстояние x _макс , площадь S , коэффициент пружины k , относительная диэлектрическая проницаемость диэлектрического слоя ε _r , и особенно плотность поверхностного заряда σ. Например, параметры материала, такие как ε _r и σ обычно оптимизируются для получения большей мощности [28, 29]. При этом оптимальное сопротивление можно отрегулировать с помощью параметров x _макс , S , и k . P _макс и оптимальное сопротивление в основном зависит от материала и параметров конструкции.

Эффективность конверсии η ТЭНов

Иногда нас больше беспокоит P _макс что мы игнорируем η . КПД - важный параметр для оценки источника питания. η определяется как соотношение между выходной электрической энергией и входящей механической энергией. Здесь мы систематически и напрямую исследовали влияние этих параметров на эффективность.

Электрическая энергия и механическая энергия получаются в соответствии с импульсом тока при оптимальном R . Выходная электрическая энергия определяется как

где промежуток времени между t _начало и t _конец выражает целостный процесс контакта и разлуки.

Расчетная механическая энергия

Таким образом, η рассчитывается следующим образом

Связь η с x _макс показан на рис. 6а. Как x _макс увеличивается, КПД η увеличивается, а затем постепенно насыщается. Мы знаем, что механическая энергия и максимальная мощность пропорциональны x _макс . Однако увеличение x _макс изменит резкость кривой текущего времени. Это означает, что скорость роста замедлится, когда x _макс больше. Влияние параметров S , k , а σ на η показаны на рис. 6б – г. Тенденция к увеличению КПД η с этими параметрами аналогичен максимальной мощности. КПД η постепенно увеличивается с S и k увеличивается. Примечательно, что σ может сильно влиять на эффективность η . Параметр ε _r трудно изменить, и, к счастью, это почти не влияет на η как показано на рис. 6e. Как показано на рис. 6f, КПД η быстро уменьшается как F увеличивается. В основном это способствует увеличению механической энергии. Очевидно, КПД сравнительно невысокий. К счастью, мы можем значительно повысить эффективность, улучшив σ.

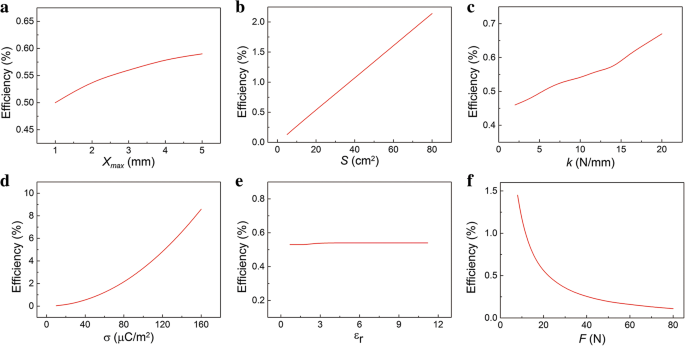
Эффективность преобразования η ТЭН. Связь рассчитанной эффективности преобразования с параметрами a x _макс , b S , c к , d σ, e ε _r , и f F

Однако на практике F может повлиять на параметр σ [30]. Под маленьким F , два слоя частично контактируют. Два слоя могут лучше контактировать, если F увеличивается. Тогда параметр F может практически повлиять на плотность поверхностного заряда σ. То есть σ увеличивается с F затем насыщается, как показано на рис. 7а. Поэтому мы пересчитали соотношение между выходной мощностью и сжимающей силой F . . Влияние F по максимальному току, напряжению и мгновенной мощности показаны на рис. 7b – d соответственно. У них похожие отношения с F . Например, выходное напряжение увеличивается на F увеличиваются, а затем остаются постоянными, что согласуется с данными экспериментов в литературе [31, 32]. Влияние F по электрической энергии показано на рис. 7д. Следует отметить, что на кривой есть точка поворота. Выходная электрическая энергия увеличивается на F увеличивается, а затем немного уменьшается. Небольшое падение выходной электрической энергии связано с более коротким процессом контакта при больших F . При небольшой сжимающей силе F пропорциональна σ, что приводит к большей выходной электрической энергии. Однако под действием большой сжимающей силы σ насыщается. Перенесенные заряды в процессе разделения остаются постоянными, в то время как в процессе контакта они уменьшаются при большей сжимающей силе. Таким образом, выходная электрическая энергия во всем процессе разделения и контакта немного падает. Связь η и F представлен на рис. 7е. Интересно, что η - F кривая имеет острый пик, максимальное значение появляется на F ≈ 50 Н. Вход E _{механический} пропорционально F , а E _{механический} намного больше, чем вывод E _{электрический} . Под маленьким F , скорость роста E _{электрический} быстрее, чем E _{механический} из-за быстрого роста σ. Однако при большом F , уменьшение E _{электрический} и увеличение E _{механический} приводят к снижению эффективности. Поворотный момент во взаимосвязи между эффективностью преобразования энергии и сжимающей силой важен при проектировании эффективного источника энергии.

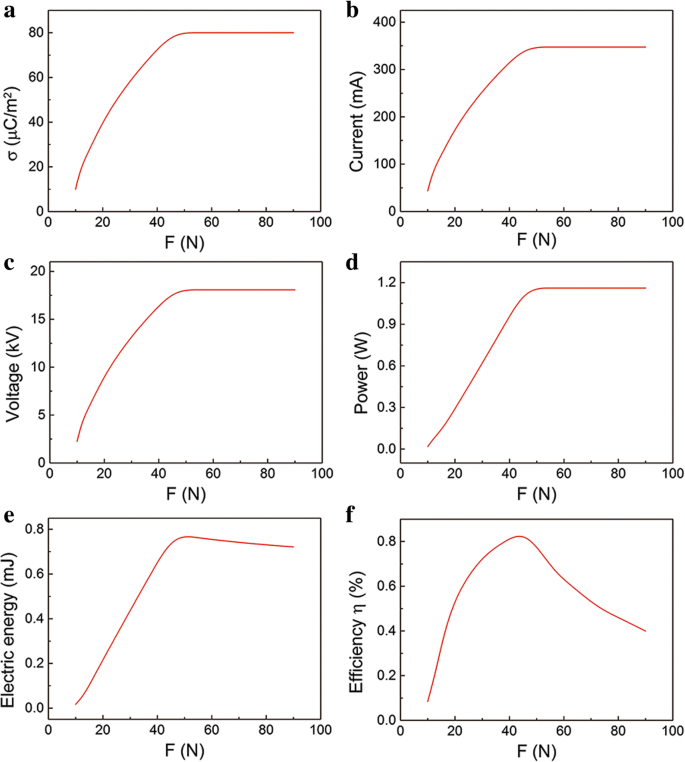
Зависимость выходной мощности от сжимающей силы F в практической ситуации. а Влияние сжимающей силы F на а плотность поверхностного заряда σ, b максимальный ток, c максимальное напряжение, d максимальная мгновенная мощность, e электрическая энергия и е эффективность

Для получения более высоких выходных характеристик, таких как ток и мгновенная мощность, большая сжимающая сила F обычно применяется. Но это может привести к низкой эффективности преобразования. Согласно приведенному выше анализу, мы можем выбрать рациональную F чтобы получить высокую мощность, а также эффективность преобразования.

Заключение

В заключение мы представили практический подход к системному и непосредственному анализу эффективности преобразования контактных ТЭНов. Выходя за рамки обычного анализа, сжимающая сила была введена для получения более универсального профиля движения, что обеспечило лучшее понимание принципа работы процесса разъединения контактов. Были представлены явные уравнения для важных характеристик устройства во всем процессе разделения и контакта, в отличие от обычного анализа, который фокусируется только на процессе разделения. Во-первых, мы проанализировали взаимосвязь выходной мощности с материалом, структурой и экспериментальными параметрами, которая в основном касалась более высокой выходной мощности. Затем, что важно, мы систематически и глубоко изучили влияние этих параметров на эффективность преобразования энергии во всем процессе. Важно отметить, что поворотный момент был обнаружен во взаимосвязи между эффективностью преобразования и силой сжатия. ТЭНы с высокой выходной мощностью и высокой эффективностью преобразования могут быть получены одновременно при оптимальном усилии. Это реалистично и полезно для более эффективных ТЭНов. Важно отметить, что у него есть хорошие шансы установить стандарты для количественной оценки эффективности TENG, которые закладывают основу для дальнейшей индустриализации и многофункциональности TENG.

Сокращения

BE:

Нижний электрод

TE:

Верхний электрод

TENGs:

Трибоэлектрические наногенераторы