Полностью диэлектрическая фазово-градиентная метаповерхность, обеспечивающая высокоэффективную аномальную передачу в ближней инфракрасной области

Введение

В последние годы метаповерхности с фазовым градиентом привлекают все большее внимание, потому что они открыли новый путь для передовой инженерии волнового фронта [1,2,3,4,5,6,7]. По сравнению с обычными устройствами управления волновым фронтом, метаповерхности с фазовым градиентом намного более гибкие, что позволяет модулировать амплитуду и фазу света [8,9,10,11]. Кроме того, как своего рода двумерный метаматериал их легче применять в области систем фотонной интеграции. Поскольку Yu et al. предложил V-образную антенную решетку в качестве фазово-градиентной метаповерхности и подробно объяснил концепцию обобщенного закона преломления [12], были предложены и исследованы различные фазово-градиентные метаповерхности, основанные на дискретных решетках наноантенн [2,3,4, 5,6,7,8,9,10,11,12,13]. Например, Liu et al. ввел золотую решетку в V-образную золотую антенную решетку, увеличив аномальную эффективность передачи в 15 раз по сравнению с без золотой решетки [14]. Фазово-градиентные метаповерхности использовались во многих областях, и их приложения включают в себя дефлекторы [8, 15, 16, 17], направленные ответвители поверхностных волн [18, 19], голографические устройства [20, 21, 22] и генераторы вихревых пучков. [23,24,25]. Хотя перспективы применения метаповерхностей на основе металлов подтверждены во многих областях, характеристики метаповерхностей обычно ограничиваются очень высокими собственными омическими потерями металлических материалов [26, 27]. Поскольку диэлектрические материалы не имеют собственных омических потерь, люди пытались заменить металлические материалы диэлектрическими материалами при разработке полностью диэлектрических метаповерхностей с высокими характеристиками [28, 29].

В последнее время общей проблемой при использовании метаповерхностей с полностью диэлектрическим фазовым градиентом была трудность в достижении высокой аномальной эффективности передачи с большим аномальным углом преломления. Чтобы решить эту проблему, Zhou et al. разработали метаповерхность, состоящую из градиентной матрицы круглых кремниевых наностержней, расположенных на кварцевой подложке, с достижением аномальной эффективности передачи 71% с аномальным углом преломления 19,27 [6]. Ян и др. разработали полностью диэлектрическую метаповерхность на основе кремниевых наноантенн для высокоэффективной аномальной передачи, аномальная эффективность передачи которой достигла 80,5% с аномальным углом преломления 29,62 [30]. В 2019 г. благодаря крестообразной структуре аномальная эффективность передачи полностью диэлектрической метаповерхности достигла 83,5% при аномальном угле преломления 30 [31]. В частности, Дэвид Селл и др. предложил и экспериментально исследовал периодическую диэлектрическую метаповерхность. В этой работе авторам удалось численно и экспериментально наблюдать аномальную рефракцию с высокой эффективностью (> 90%) для углов выхода до 50 [32]. Кроме того, некоторые исследователи использовали преимущества гиперболических метаматериалов с широкополосным диапазоном и высоким двулучепреломлением для достижения высокой эффективности передачи [33, 34].

В этой работе наша цель - разработать полностью диэлектрическую метаповерхность, чтобы одновременно получить высокую эффективность аномальной передачи и увеличить угол аномального преломления. Предлагаемая метаповерхность состоит из прерывистых правильных гексагональных кремниевых наностержней, поддерживаемых кремнеземной подложкой. Мы систематически анализируем аномальную эффективность передачи и аномальный угол преломления предлагаемой структуры с помощью метода конечных разностей во временной области (FDTD). Результаты показывают, что на центральной длине волны 1529 нм общая эффективность передачи диэлектрической метаповерхности может достигать 96,5%; кроме того, секция желаемой аномальной эффективности передачи может достигать 96,2% с аномальным углом преломления 30,64. Угол аномального преломления можно увеличить, регулируя количество элементов на периодический интервал и период. Мы численно демонстрируем аномальный угол преломления, который достигает 68,58 с аномальной эффективностью передачи до 69,7% для центральной длины волны 1536 нм. Считается, что предложенная полностью диэлектрическая метаповерхность будет играть жизненно важную роль в современной инженерии волнового фронта.

Дизайн и методы

Для метаповерхности с фазовым градиентом геометрическая морфология и параметры сильно влияют на производительность устройства. Как показано на рис. 1, мы сначала исследуем простую матричную структуру, состоящую из правильных гексагональных наностержней на основе кремнеземной подложки. Эффективность передачи и фазовые распределения простой структуры массива анализируются с использованием метода FDTD. В моделировании x - и y -направления задаются как периодические граничные условия, а z -направление задано как идеально согласованные слои. Мы устанавливаем нормальную поперечную электрическую волну падающей на дно. Направление электрического поля падающего света вдоль y -направление, диапазон длин волн 1400–1600 нм. При численном анализе показатели преломления кремния и кремнезема взяты из данных, предложенных Паликом [35]. Экспериментально, чтобы изготовить подложку из диоксида кремния полуограниченного размера, необходимо выполнить процесс травления. Нам также необходимо нанести кремниевую пленку толщиной 1200 нм поверх кремнеземной подложки с помощью метода химического осаждения из паровой фазы при низком давлении (LPCVD). Силиконовая пленка покрывается центрифугированием фоторезистом ZEP520A, а затем наносится тонкий слой Cr в качестве резиста. Гексагональные диэлектрические наностержни могут быть получены с помощью электронно-лучевой литографии (ЭЛС). Наконец, удалитель 1165 и плазма \ (O_2 \) используются для удаления фоторезиста, в результате чего получается спроектированная полностью диэлектрическая метаповерхность с фазовым градиентом [4, 6]. Однако поперечное сечение регулярных гексагональных наностержней может напоминать круг из-за эффектов близости при практическом экспериментальном изготовлении. Чтобы решить эту проблему, мы можем настроить коррекцию эффекта близости (PEC) и дозу EBL в соответствии с морфологией образца. Мы считаем, что, корректируя схему, мы в конечном итоге сможем получить точно изготовленные правильные шестиугольные метаповерхности.

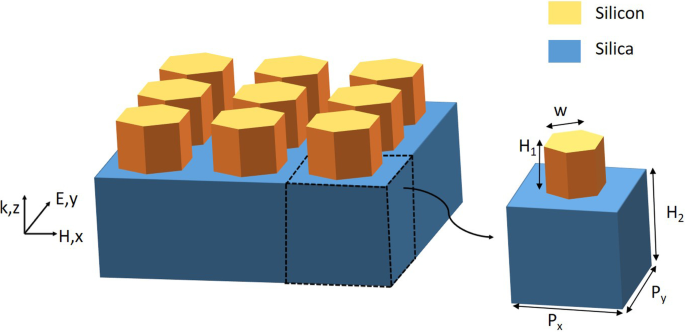
Схема простой матричной структуры, состоящей из правильных гексагональных кремниевых наностержней на кремнеземной подложке

В отличие от идеальной границы, когда свет распространяется через метаповерхность, оптические свойства, такие как состояние поляризации, фаза и волновой фронт, существенно меняются. Мы не можем объяснить эти явления с помощью классического закона Снеллиуса в геометрической оптике, когда электромагнитные волны распространяются через эти границы раздела, что приводит к универсальному обобщенному закону Снеллиуса [8,9,10,11,12]. Согласно обобщенному закону Снеллиуса, аномальное отражение или преломление на границе раздела двух сред происходит из-за горизонтального распределения фазы. Мы можем выразить два типа рефракции как

где \ (\ theta _r \) представляет угол преломления или угол аномального преломления, а \ (\ theta _i \) представляет угол падения. Показатель преломления \ (n_r \) обычно относится к показателю преломления воздуха, который имеет величину 1. Напротив, \ (n_i \) относится к показателю преломления материала метаповерхности, \ (\ lambda _0 \) равен рабочая длина волны в свободном пространстве, а d \ (\ phi \) / \ ({\ text {d}} x \) - фазовый градиент. Фазово-градиентной метаповерхности необходимо достичь полного почти линейного сдвига фазы \ (2 \ pi \) за большой период, чтобы управлять аномальной передачей; таким образом, фазовый градиент

где \ (P_x \) - период предлагаемой метаповерхности вдоль x -ось. В этой работе мы рассматриваем только нормальный свет, падающий на границу раздела; таким образом, \ (\ theta _i \) равно 0, и уравнение можно упростить как

Фазово-градиентные метаповерхности демонстрируют аномальное пропускание не только низкого порядка, но и аномальное пропускание высокого порядка. Чтобы определить угол аномального преломления высокого порядка, мы вводим уравнение решетки для модификации обобщенного закона Снеллиуса [36,37,38]. Модифицированный обобщенный закон Снеллиуса

где м представляет собой традиционный порядок дифракции. Сдвиги электромагнитной волны из положения исходного нулевого порядка в положение первого порядка можно использовать для определения угла аномального преломления. Кроме того, период и рабочая длина волны определяют общее количество порядков дифракции. Отношение \ (\ lambda _0 \) к \ (P_x \) влияет на желаемое значение m. Когда \ (\ lambda _0 \) / \ (P_x \) больше 0,5, m может принимать только значение 0, и в этом случае можно получить только три порядка дифракции:0, −1 и 1. Однако, когда \ (\ lambda _0 \) / \ (P_x \) меньше 0,5, м может принимать значение 0 или 1, и в этом случае можно получить пять порядков дифракции:\ (- 2, -1, 0, 1 \) и 2. В следующем обсуждении эта теория подтверждается нашими расчетными результатами. .

Чтобы объяснить характеристики предлагаемой структуры, мы в основном рассчитываем эффективность и угол преломления для аномального пропускания. Общая эффективность передачи и аномальная эффективность передачи определяются как

где \ (I _ {\ mathrm {in}} \) - входная интенсивность, \ (I _ {\ mathrm {out}} \) - полная интенсивность передачи, а \ (I_r \) - передаваемая интенсивность вдоль аномальной рефракции. угол.

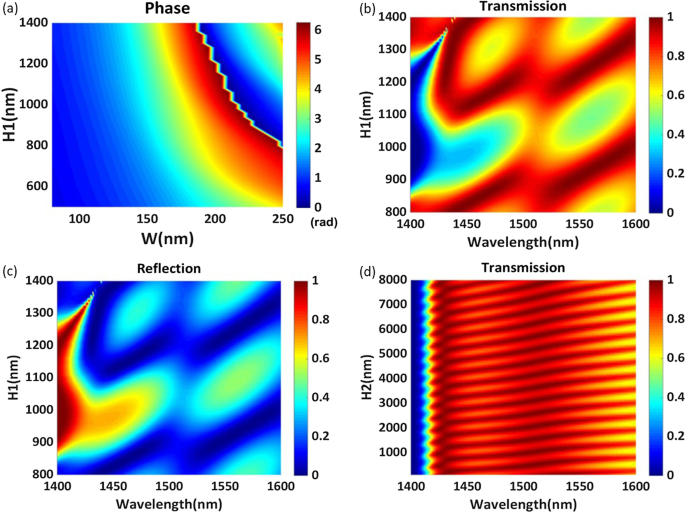
а Фаза периодических регулярных гексагональных наностержней для различных структурных параметров \ (H_1 \) и w на длине волны 1529 нм. б Эффективность передачи и c эффективность отражения периодической структуры для различной толщины \ (H_1 \) в диапазоне длин волн 1400–1600 нм. г Эффективность пропускания периодической структуры для различной толщины \ (H_2 \) в диапазоне длин волн 1400–1600 нм

Для предлагаемой конструкции мы надеемся достичь полного сдвига фазы на 2 \ (\ pi \), регулируя высоту \ (H_1 \) и длину стороны правильного шестиугольника w . Устанавливаем период P до 500 нм и установите толщину подложки \ (H_2 \) на 7050 нм. Поскольку толщина подложки \ (H_2 \) больше, чем \ (4 \ lambda \), мы можем рассматривать подложку как полубесконечную подложку. Вариации фазы с изменением \ (H_1 \) и w на длине волны 1529 нм показаны на рис. 2а. Понятно, что фаза проходящего света зависит от длины стороны правильного шестиугольника w , но только когда высота \ (H_1 \) больше 800 нм, эта структура может реализовать полный фазовый сдвиг на 2 \ (\ pi \). Высокая эффективность передачи - еще один фактор, который необходимо учитывать при проектировании метаповерхностей с фазовым градиентом. На рис. 2b, c показаны изменения эффективности передачи и эффективности отражения в зависимости от длины волны для разной высоты \ (H_1 \) периодических наностержней, показанных на рис. 1. Структурный параметр w установлен на 160 нм. Как показано на рис. 2b, длина волны пика эффективности передачи смещается в красную сторону с увеличением высоты наностержня. Очевидно, что высота наностержней оказывает заметное влияние на эффективность передачи и эффективность отражения. Здесь для получения высокой эффективности передачи высота \ (H_1 \) установлена ​​на 1200 нм. При этом значении максимальная эффективность передачи простой однородной метаповерхности достигает 98,70% на длине волны 1540 нм. На рис. 2г показано изменение эффективности передачи в зависимости от длины волны для разных высот \ (H_2 \). Эффективность передачи периодически меняется с увеличением толщины подложки \ (H_2 \).

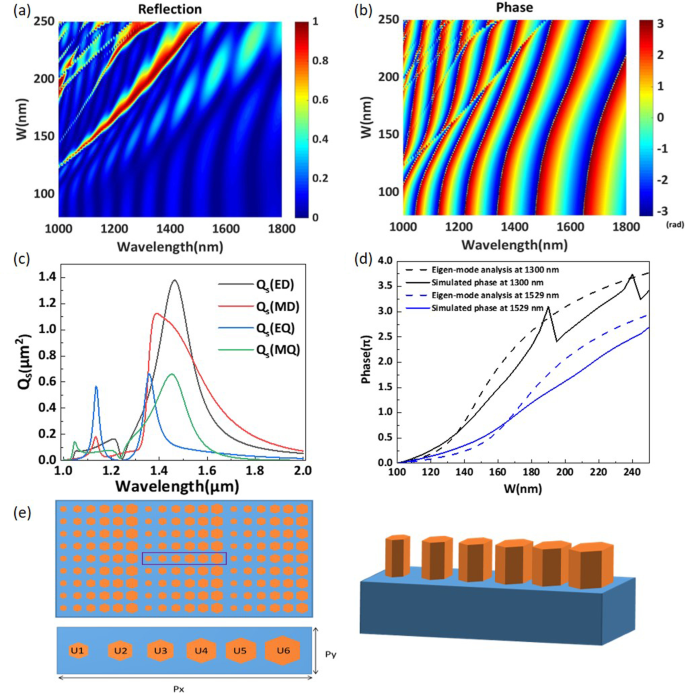
а Эффективность отражения и b фаза периодических регулярных гексагональных наностержней для разных значений w в диапазоне длин волн 1000–1800 нм. c Сечение рассеяния \ (Q_s \) в зависимости от длины волны изолированного регулярного гексагонального кремниевого наностержня. Показан вклад каждого члена в разложение Ми. г Фазовые профили, полученные с помощью анализа собственных мод и численного моделирования для переменной длины стороны w . е Схема разработанной фазово-градиентной метаповерхности

На рис. 3a, b показано изменение эффективности отражения и фазы простой решетчатой ​​структуры путем изменения длины стороны правильных шестиугольников для диапазона длин волн 1000–1600 нм. Как показано на рис. 3a, b, в спектре отражения имеется много различимых резонансных пиков. Благодаря простой структуре решетки можно реализовать фазовый сдвиг, близкий к \ (\ pi \), для каждой резонансной длины волны. Понятно, что полный сдвиг фазы \ (2 \ pi \) может быть достигнут, если длина стороны правильного шестиугольника w изменяется от 100 до 220 нм на длине волны 1529 нм. Чтобы дополнительно прояснить механизм фазового сдвига \ (2 \ pi \), мы используем метод электромагнитного мультипольного разложения (EME) для расчета сечений рассеяния (SCS) изолированного регулярного гексагонального кремниевого наностержня [31, 41]. На рис. 3c показаны рассчитанные SCS рассеяния электрического диполя (ED), магнитного диполя (MD), электрического квадрупольного (EQ) и магнитного квадрупольного (MQ) компонентов для w =160 нм. Очевидно, что на рабочей длине волны возбуждаются различные резонансы Ми, особенно дипольные. Однако есть некоторые отклонения между возбуждением резонансов Ми в изолированной частице и в периодических частицах. На длине волны 1529 нм нет резкого изменения фазы, что доказывает, что фазовый сдвиг \ (2 \ pi \) формируется только одной модой. Поэтому механизм контроля фазы \ (2 \ pi \) на длине волны 1529 нм анализируется с помощью анализа собственных мод [42]. Эти наностержни можно рассматривать как низкокачественные резонаторы Фабри – Перо, а фаза может модулироваться эффективным показателем преломления основной моды. Таким образом, фаза может быть продемонстрирована

где \ (H_1 \) - высота этих наностержней, \ (n _ {\ mathrm {eff}} \) - эффективный показатель преломления основной моды, полученный анализом собственных мод, а \ (\ lambda \) - рабочая длина волны . На рис. 3d мы построили фазовые профили, полученные с помощью анализа собственных мод (пунктирная линия) и численного моделирования (сплошная линия) на длинах волн 1300 нм и 1529 нм, соответственно. Как показано на рис. 3d, в моделируемой фазе на длине волны 1300 нм происходит два резких уменьшения фазы, соответствующих двум видам резонансов Ми. Когда w изменяется от 100 до 250 нм, тенденции изменения фазы, полученные двумя методами, в основном одинаковы на длине волны 1529 нм. Согласно красному смещению пиков отражения на рис. 3а, когда w больше 250 нм, резонанс Ми возбуждается на длине волны 1529 нм. Для метаповерхности, которую мы предлагаем в этой работе, поскольку структурные параметры каждого элемента находятся в диапазоне от 100 до 220 нм, как показано в таблице 1, в этом диапазоне не возбуждаются резонансы Ми. Поэтому можно предположить, что фазовый сдвиг в основном основан на резонансе Фабри – Перо [6, 39, 40, 42]. Согласно обобщенному закону Снеллиуса, аномальная передача может быть достигнута, если метаповерхность имеет способность сдвига фазы \ (2 \ pi \). Регулируя размер наностержней так, чтобы фазовый сдвиг был равномерно распределен и охватывал полный диапазон \ (2 \ pi \), мы можем отклонить луч, смещая его волновой фронт. Рисунок 3e иллюстрирует схематическую диаграмму метаповерхности фазового градиента. Шесть кремниевых наностержней разного размера с фазовыми интервалами \ (2 \ pi / 5 \) расположены на кремнеземной подложке, чтобы сформировать полный фазовый градиент от 0 до \ (2 \ pi \). Фиолетовая рамка представляет собой полный период, а \ (P_x \) и \ (P_y \) установлены на 3000 нм и 500 нм соответственно.

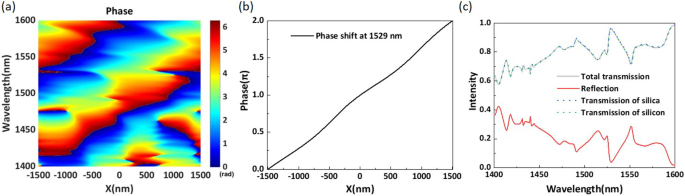
а Смоделированный фазовый сдвиг метаповерхности по x -направление в полном периоде для диапазона длин волн 1400–1600 нм. б Смоделированное распределение фазы по x -направление на длине волны 1529 нм. c Смоделированные интенсивности проходящего и отраженного света

Результаты и обсуждение

В таблице 1 приведены структурные параметры каждого элемента предлагаемой конструкции. Мы исследуем фазовое распределение и интенсивность проходящего света. Для облегчения анализа мы устанавливаем начало координат как центр суперячейки. Мы моделируем фазовое распределение проходящего света в диапазоне длин волн 1400–1600 нм. Как показано на рис. 4а, предложенная структура может реализовать полный фазовый сдвиг \ (2 \ pi \) в диапазоне 1400–1600 нм. Чтобы прояснить это, на рис. 4b показана кривая фазового сдвига на центральной длине волны 1529 нм. Как показано на рис. 4b, фазовый сдвиг показывает линейную тенденцию и очень плавный. Согласно обобщенному закону Снеллиуса, чем лучше линейность фазового сдвига, тем более плоская фазовая плоскость проходящего света. Мы моделируем коэффициент пропускания и отражения предлагаемой метаповерхности для диапазона 1400–1600 нм, результаты которого показаны на рис. 4c. Наблюдая за кривой, мы видим, что общее пропускание остается очень эффективным, превышая 60% во всем рабочем диапазоне длин волн. На длине волны 1529 нм общая эффективность передачи достигает 96,5% с эффективностью отражения 3,4%. Сумма отражательной способности структуры и пропускания кремнеземной подложки составляет 1 во всем диапазоне длин волн. Следовательно, мы можем определить, что отражение в основном происходит на первой границе раздела между воздухом и подложкой. Как показано на рис. 4c, различия между тремя кривыми пропускания едва заметны и вызваны поглощением структуры. Скорость поглощения намного меньше 0,1%, потому что мнимая часть показателя преломления кремния в ближнем инфракрасном диапазоне длин волн очень мала. Таким образом, скорость поглощения незначительна. Эффективность передачи и эффективность отражения имеют противоположные тенденции по сравнению с длиной волны, и потери структуры в основном происходят из-за отражения. Ясно, что предложенная метаповерхность с фазовым градиентом может реализовать полный почти линейный \ (2 \ pi \) фазовый сдвиг и одновременно поддерживать более высокую эффективность передачи в диапазоне 1400–1600 нм.

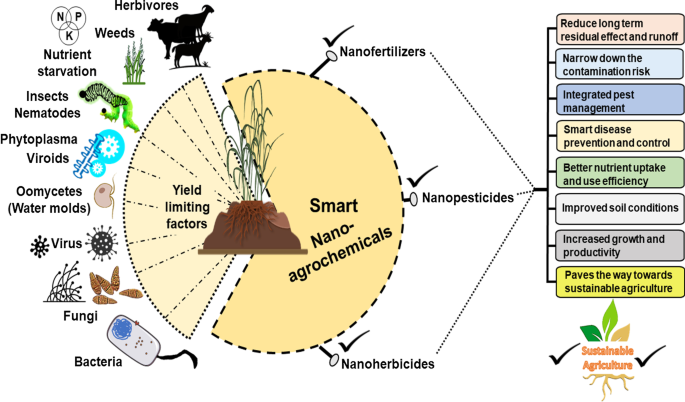
а Смоделированная интенсивность аномальной эффективности передачи. б Эффективность передачи в дальней зоне для различных углов аномального преломления на длине волны 1529 нм. c Фазовое распределение конфигурации метаповерхности на длине волны 1529 нм. Угол на рисунке показывает угол преломления аномально прошедшего света

Как показано на рис. 5а, мы также вычисляем желаемую эффективность аномальной передачи метаповерхности с фазовым градиентом во всем рабочем диапазоне длин волн и нормируем ее на энергию падающего света. Сравнивая рис. 4c с рис. 5a, мы видим, что тенденции общей эффективности передачи и аномальной эффективности передачи в зависимости от длины волны совпадают. Результаты показывают, что желаемая эффективность аномального пропускания превышает 80% в диапазонах длин волн 1527–1545 и 1591–1600 нм. Примечательно, что аномальная эффективность передачи достигает 96,2% на длине волны 1529 нм. На рисунке 5b показана зависимость между эффективностью передачи в дальней зоне и аномальным углом преломления на длине волны 1529 нм. Ясно, что энергия дальнего поля проходящего света в основном сосредоточена под углом 30,64, и только слабая энергия распределяется под двумя другими углами. Для удобства наблюдения на рис. 5c показано фазовое распределение конфигурации метаповерхности на центральной длине волны. Из рис. 5в видно, что проходящий свет явно преломляется и фронт волны относительно плоский. Подставив рабочую длину волны и период структуры в уравнение. (3), мы получаем аномальный угол передачи \ (\ theta _r \) 30,642, что очень близко к результатам нашего моделирования. Чтобы проверить связь между числом порядков дифракции и отношением длины волны к периоду, мы устанавливаем \ (\ lambda _0 \) / \ (P_x \) на критическое значение 0,5 и выбираем пять различных длин волн для выполнения теоретических расчетов. и моделирование FDTD. Результаты показаны в Таблице 2. Очевидно, что результаты моделирования очень согласуются с расчетными результатами.

Согласно расчетным и смоделированным углам для предложенной структуры, показанной в таблице 2, когда \ (\ lambda _0 \) / \ (P_x \) больше 0,5, присутствуют только дифракционный порядок 0 и дифракционный порядок 1, и нет порядок дифракции 2. Когда \ (\ lambda _0 \) / \ (P_x \) меньше 0,5, при моделировании получаются порядки дифракции 0, 1 и 2. Этот результат полностью согласуется с теоретическим анализом, описанным выше, и, таким образом, полностью подтверждает надежность обобщенного закона Снеллиуса в сочетании с теорией решеток.

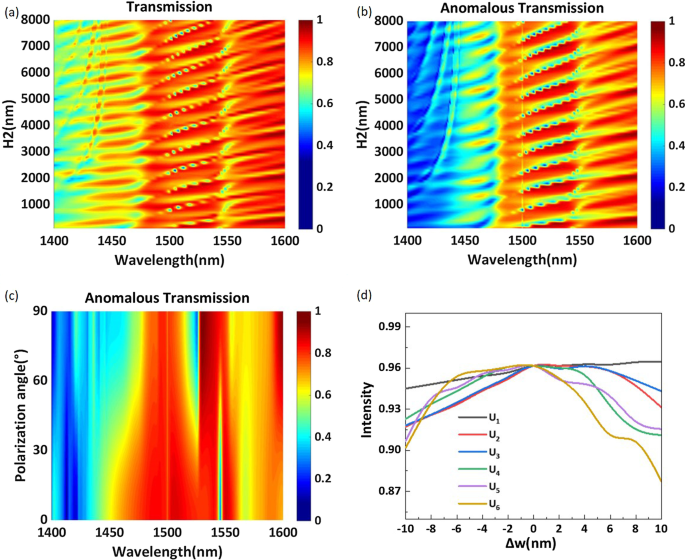
а Общая эффективность передачи и b аномальная эффективность пропускания как функция толщины подложки для диапазона длин волн 1400–1600 нм. c Аномальная эффективность пропускания предложенной структуры для разных углов поляризации в диапазоне длин волн 1400–1600 нм. г Расчетная аномальная эффективность передачи при различных значениях длины стороны w

На рис. 6а, б диапазон длин волн составляет 1400–1600 нм, а полная эффективность передачи и аномальная эффективность передачи показаны как функция толщины подложки \ (H_2 \). На эффективность передачи влияет толщина подложки, а длина волны пика смещается в красную сторону с увеличением толщины. Очевидно, что как общая эффективность передачи, так и аномальная эффективность передачи периодически изменяются с увеличением толщины подложки. Чтобы уменьшить потребление памяти при компьютерном моделировании, оптимизированная толщина подложки установлена ​​равной 7050 нм, а желаемая эффективность аномальной передачи достигает 96,2% на длине волны 1529 нм. Мы полагаем, что высокая эффективность аномального пропускания может быть получена даже при толстой подложке. Мы также вычисляем изменение аномальной эффективности передачи в зависимости от угла поляризации падающего света, как показано на рис. 6c. На длине волны 1529 нм аномальная эффективность передачи увеличивается с увеличением угла поляризации и достигает максимума, когда угол поляризации равен 90 ( y -поляризация). Учитывая, что длина стороны w структуры требует точных числовых значений и может быть трудно точно изготовить, мы рассчитываем аномальную эффективность передачи при различных значениях w проверить переносимость конструкции. Как показано на рис. 6d, допуск конструкции достигается изменением длины стороны w на основе структурных параметров, перечисленных в таблице 1. Эти кривые, \ (U_1 \) - \ (U_6 \), представляют изменение аномальной эффективности передачи с длинами сторон шести наностержней на периодический интервал. Горизонтальная ось \ (\ Delta w \) представляет разницу между смоделированной длиной стороны и длиной стороны, указанной в таблице 1. Мы видим, что кривая \ (U_1 \) очень плоская и что аномальная эффективность передачи изменяется только на 2 % с длиной стороны в пределах ширины полосы 20 нм. Тенденции кривых \ (U_2 \), \ (U_3 \), \ (U_4 \) и \ (U_5 \) в основном одинаковы, и может быть получена аномальная эффективность передачи более 90%, когда длина стороны находится в пределах полоса пропускания 20 нм. Очевидно, что изменение длины стороны \ (U_6 \) оказывает наиболее заметное влияние на производительность; тем не менее, \ (U_6 \) по-прежнему демонстрирует высокую аномальную эффективность передачи. Когда длина стороны уменьшается на 10 нм, аномальная эффективность передачи остается выше 90%. Когда длина стороны увеличивается на 10 нм, аномальная эффективность передачи заметно снижается, но она по-прежнему превышает 87%. Эти результаты доказывают, что небольшая ошибка во время производства существенно не влияет на характеристики метаповерхности.

Это видно из уравнения. (3) на угол дифракции света с аномальным пропусканием влияет \ (\ lambda _0 \) / \ (P_x \); таким образом, мы пытаемся изменить величину \ (P_x \), чтобы получить разные углы аномального преломления. Эффективным методом реализации различных углов аномального преломления является изменение количества элементов в периодическом интервале. Поэтому мы продолжаем проектировать метаповерхности фазового градиента с несколькими наборами. Элементов метаповерхности за периодический интервал изменяется от трех до девяти. Мы выбираем рабочую длину волны с наивысшей аномальной эффективностью передачи для каждой группы метаповерхностей и наблюдаем фазовое распределение проходящего света. Результаты моделирования представлены на рис. 7a – f. По мере того, как количество элементов уменьшается с девяти до трех, отношение \ (\ lambda _0 \) / \ (P_x \) постепенно увеличивается, а угол аномального пропускания увеличивается с 19,35 до 68,58. На рис. 7a – f показано, что метаповерхности с фазовым градиентом с различными элементами могут реализовывать почти линейное фазовое распределение и что волновой фронт проходящего света относительно гладкий. Мы проводим анализ вышеупомянутых конфигураций в дальней зоне и строим график распределения энергии прошедшего света вдоль каждого угла дифракции, как показано на рис. 8a – f. Мы можем получить более 80% аномальной эффективности передачи от 19,35 до 46,68. Структурные параметры каждого элемента и подробные численные результаты перечислены в таблице 3. В нашем процессе оптимизации длина стороны правильного шестиугольника w и период P являются основными параметрами оптимизации.

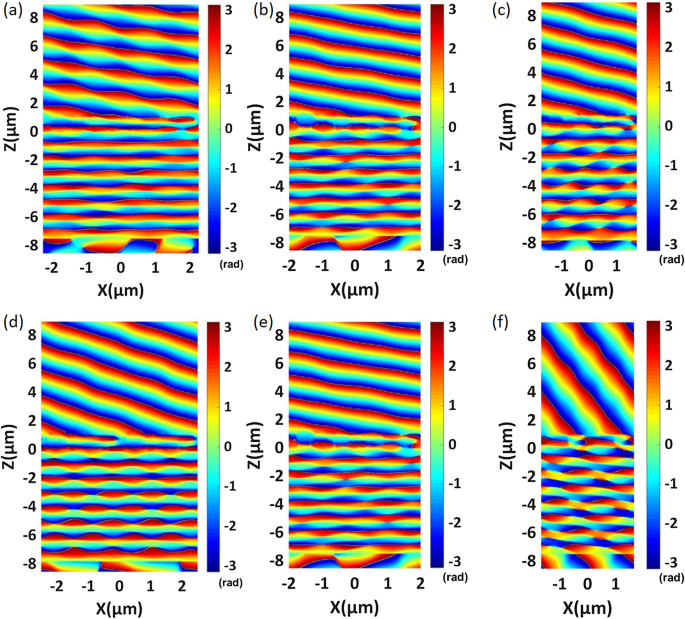
Фазовое распределение фазово-градиентной метаповерхности, состоящей из разных номеров элементов. а Девятиэлементная метаповерхность. б Восьмиэлементная метаповерхность. c Семиэлементная метаповерхность. г Пятиэлементная метаповерхность. е Четырехэлементная метаповерхность. е Трехэлементная метаповерхность. г - е изобразите два периода, чтобы лучше показать эффект аномальной передачи. Подробные параметры показаны в Таблице 3

Интенсивности пропускания в дальнем поле под разными углами фазово-градиентных метаповерхностей, состоящих из разных номеров элементов. а - е представляют девять, восемь, семь, пять, четыре и три элемента соответственно

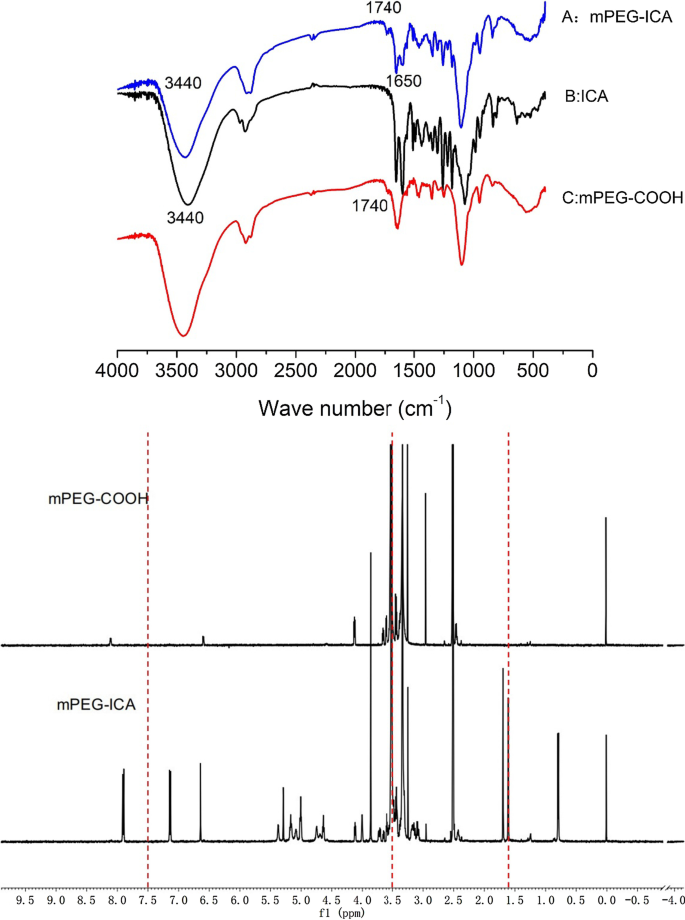
а Смоделированное изменение фазы большой угловой метаповерхности вдоль x -направление в полном периоде для длин волн 1400–1600 нм. б Полный \ (2 \ pi \) сдвиг фазы по x -направление фазово-градиентной метаповерхности на 1450, 1500, 1536 и 1550 нм. c Интенсивность полной передачи и аномальной передачи

According to the generalized Snell’s Law, to design a larger anomalous refraction angle \(\theta _r\), we should increase the ratio of the working wavelength \(\lambda\) to the structural period \(P_x\). As shown in Fig. 9a, we plot the phase variation of the transmitted light along the x -direction for wavelengths of 1400–1600 nm. For clarity, we select four wavelength points, i.e., 1450 nm, 1500 nm, the central working wavelength 1536 nm, and 1550 nm, to plot the phase shift curves shown in Fig. 9b. It is clear that the all-dielectric metasurface can realize a full \(2\pi\) phase shift for the wavelength points. From Fig. 9b, we can see that the phase variation shows a linear trend along the x -direction. We calculate the total transmission efficiency and the desired anomalous transmission efficiency of the structure in the working band, the results of which are shown in Fig. 9c. It can be observed that the total transmission efficiency is lower than before. However, at the operating wavelength of 1536 nm, the anomalous transmission efficiency can reach 69.6% with an anomalous refraction angle of 68.58. The phase distribution of transmitted light and the energy distributions at different anomalous refraction angles are shown in Figs. 7f and 8f, respectively. From the electric field distribution, we can clearly see that the equilateral phase plane of the transmitted light is very flat. The transmitted light emits very little energy at 0 and \(-68.58\), and the majority of transmitted light is concentrated at 68.58. The anomalous transmission performance of the all-dielectric phase-gradient metasurface designed by us is better than that of most of the metasurface structures proposed before, and the anomalous transmission efficiency can reach more than 60% within the range of anomalous refraction angles from 0 to 70. Based on the above analysis, an anomalous refraction angle of approximately 30 is the most reasonable. At this anomalous refraction angle, the highest anomalous transmission efficiency can be achieved, and the anomalous refraction angle can be guaranteed to be large enough.

Conclusions

In summary, we designed and numerically investigated an all-dielectric phase-gradient metasurface to achieve high-efficiency anomalous transmission in the near-infrared region. The metasurface consists of regular hexagonal silicon nanorods arranged on a silica substrate. The FDTD method was used to calculate the transmission efficiency and anomalous refraction angle of the transmitted light. The results show that the metasurface can realize a complete \(2\pi\) phase shift in the wavelength range of 1400–1600 nm. At a center wavelength of 1529 nm, the desired anomalous transmission efficiency reached 96.2% with an anomalous refraction angle of 30.64. Furthermore, the anomalous transmission efficiency exceeded 80% in the range of 1527–1545 nm, which means that our design is more flexible. We also designed multiple sets of phase-gradient metasurfaces by changing the number of elements per periodic interval and adjusting the period of the metasurface. The optimized results show that we can modulate the anomalous refraction angle in the range of 19.35-68.58. When the anomalous refraction angle is less than 46.68, more than 80% of the anomalous transmission efficiency can be obtained. Such an all-dielectric metasurface will be easy to apply to integrated optical devices.

Доступность данных и материалов

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

Сокращения

FDTD:

Finite difference time domain

TE:

Transverse electric

LPCVD:

Low-pressure chemical vapor deposition

EBL:

Электронно-лучевая литография

PEC:

Proximity effect correction

EME:

Electromagnetic multipole expansion

SCSs:

Scattering cross sections

ED:

Electric dipole

MD:

Magnetic dipole

EQ:

Electric quadrupole

MQ:

Magnetic quadrupole