Понимание локальных минимумов в обучении нейронной сети

В этой статье обсуждается осложнение, которое может помешать вашему персептрону достичь адекватной точности классификации.

В серии статей о нейронных сетях AAC мы рассмотрели широкий круг вопросов, связанных с пониманием и разработкой многослойных нейронных сетей Perceptron. Прежде чем читать эту статью о локальных минимумах, ознакомьтесь с остальной частью серии ниже:

1. Как выполнить классификацию с помощью нейронной сети:что такое перцептрон?
2. Как использовать простой пример нейронной сети персептрона для классификации данных
3. Как обучить базовую нейронную сеть персептрона
4. Общие сведения об обучении простой нейронной сети
5. Введение в теорию обучения нейронных сетей.
6. Скорость обучения в нейронных сетях
7. Расширенное машинное обучение с многоуровневым персептроном
8. Функция активации сигмовидной кишки:активация в многослойных перцептронных нейронных сетях.
9. Как обучить многослойную нейронную сеть персептрона
10. Понимание формул обучения и обратного распространения ошибки для многослойных персептронов
11. Архитектура нейронной сети для реализации Python
12. Как создать многослойную нейронную сеть персептрона на Python.
13. Обработка сигналов с использованием нейронных сетей:проверка при проектировании нейронных сетей
14. Обучающие наборы данных для нейронных сетей:как обучить и проверить нейронную сеть Python
15. Сколько скрытых слоев и скрытых узлов нужно нейронной сети?
16. Как повысить точность нейронной сети скрытого уровня
17. Включение узлов смещения в вашу нейронную сеть
18. Понимание локальных минимумов в обучении нейронной сети

Обучение нейронной сети - сложный процесс. К счастью, нам не нужно полностью понимать это, чтобы извлечь из этого пользу:сетевая архитектура и процедуры обучения, которые мы используем, действительно приводят к созданию функциональных систем, которые достигают очень высокой точности классификации. Однако есть один теоретический аспект обучения, который, несмотря на то, что он несколько сложен, заслуживает нашего внимания.

Назовем это «проблемой локальных минимумов».

Почему местные минимумы заслуживают нашего внимания?

Ну ... я не уверен. Когда я впервые узнал о нейронных сетях, у меня сложилось впечатление, что локальные минимумы действительно являются серьезным препятствием для успешного обучения, по крайней мере, когда мы имеем дело со сложными отношениями ввода-вывода. Однако я считаю, что недавние исследования преуменьшают важность локальных минимумов. Возможно, новые сетевые структуры и методы обработки снизили серьезность проблемы, или, возможно, мы просто лучше понимаем, как нейронные сети на самом деле перемещаются к желаемому решению.

Мы вернемся к текущему состоянию локальных минимумов в конце этой статьи. А пока я отвечу на свой вопрос следующим образом:локальные минимумы заслуживают нашего внимания, потому что, во-первых, они помогают нам более глубоко задуматься о том, что на самом деле происходит, когда мы обучаем сеть с помощью градиентного спуска, а во-вторых, потому что локальные минимумы - или по крайней мере были —Считал серьезным препятствием на пути успешного внедрения нейронных сетей в реальные системы.

Что такое местный минимум?

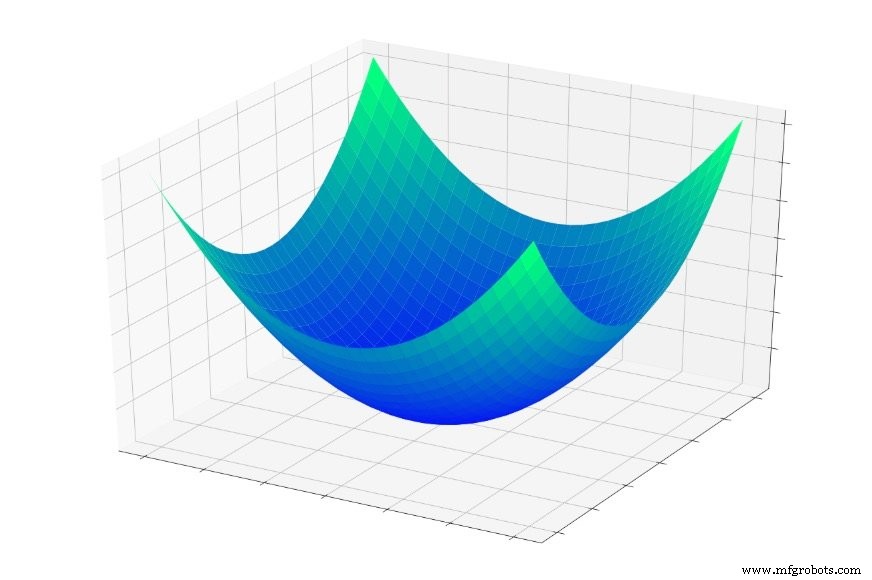
В Части 5 мы рассматривали «чашу ошибок», показанную ниже, и я описал тренировку как поиск самой нижней точки в этой чаше.

( Примечание :На протяжении всей статьи мои изображения и пояснения будут основываться на нашем интуитивном понимании трехмерных структур, но имейте в виду, что общие концепции не ограничиваются трехмерными отношениями. Действительно, мы часто используем нейронные сети, размерность которых намного превышает две входные переменные и одну выходную переменную.)

Если бы вы прыгнули в эту чашу, вы бы каждый раз соскользнули на дно. С чего бы вы ни начали , вы попадете в самую низкую точку всей функции ошибок. Эта самая низкая точка - глобальный минимум . . Когда сеть достигла глобального минимума, она оптимизировала свою способность классифицировать обучающие данные и теоретически , это основная цель обучения:продолжать изменять веса до тех пор, пока не будет достигнут глобальный минимум.

Однако мы знаем, что нейронные сети способны аппроксимировать чрезвычайно сложные отношения ввода-вывода. Вышеупомянутая чаша ошибок не совсем подходит к категории «чрезвычайно сложных». Это просто график функции \ (f (x, y) =x ^ 2 + y ^ 2 \).

Но теперь представьте, что функция ошибки выглядит примерно так:

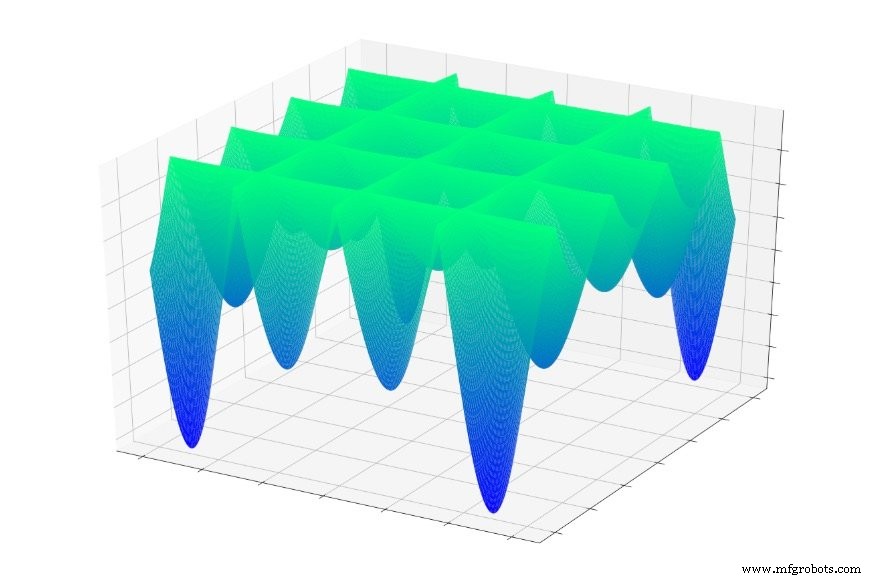
Или это:

Или это:

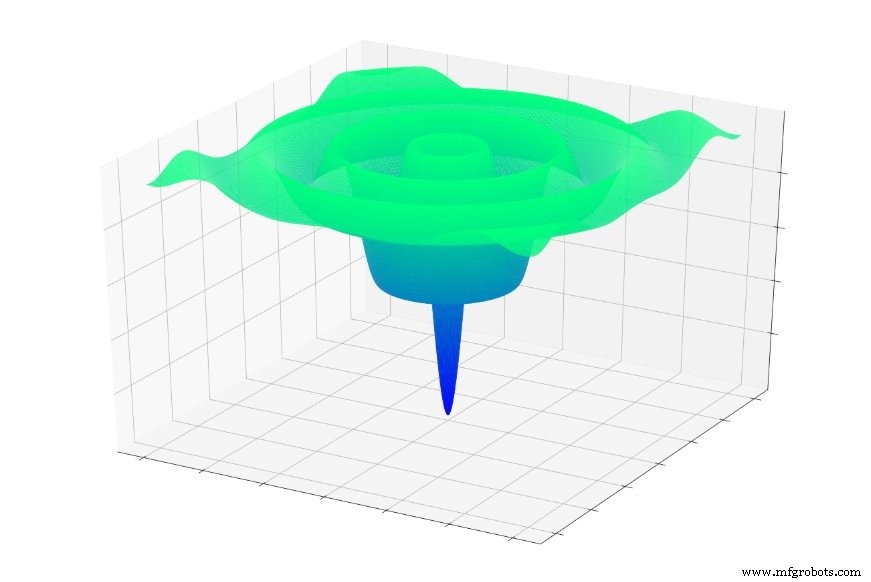
Если вы случайно перейдете к одной из этих функций, вы часто скатитесь до локального минимума. Вы будете в самой нижней точке локализованной части графика, но вы можете быть далеко от глобального минимум.

То же самое может случиться с нейронной сетью. Градиентный спуск основан на локальном информация, которая, как мы надеемся, приведет сеть к глобальному минимум. Сеть не имеет предварительных сведений о характеристиках общей поверхности ошибки и, следовательно, о том, когда она достигает точки, которая кажется нижней частью поверхности ошибки на основе локальной информации , он не может вытащить топографическую карту и решить, что ему нужно вернуться в гору чтобы найти точку, которая на самом деле ниже, чем все остальные.

Когда мы реализуем базовый градиентный спуск, мы говорим сети:«Найдите дно поверхности ошибки и оставайтесь там». Мы не говорим:«Найдите дно поверхности с ошибкой, запишите свои координаты, а затем продолжайте идти вверх и вниз, пока не найдете следующую». Дай мне знать, когда закончишь ».

Действительно ли мы хотим найти глобальный минимум?

Разумно предположить, что глобальный минимум представляет собой оптимальное решение, и заключить, что локальные минимумы проблематичны, потому что обучение может «застопориться» на локальном минимуме, а не продолжать движение к глобальному минимуму.

Я думаю, что это предположение справедливо во многих случаях, но недавнее исследование поверхностей потерь нейронных сетей предполагает, что сети высокой сложности могут действительно выиграть от локальных минимумов, потому что сеть, которая находит глобальный минимум, будет перетренирована и, следовательно, будет меньше эффективен при обработке новых входных выборок.

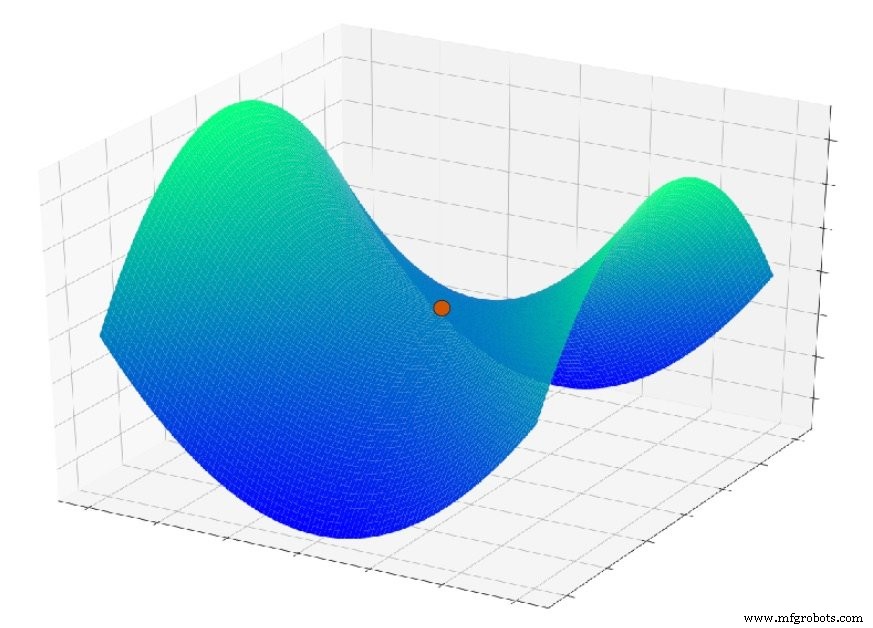
Еще одна проблема, которая здесь возникает, - это поверхностный элемент, называемый седловой точкой; вы можете увидеть пример на графике ниже. Возможно, что в контексте реальных нейросетевых приложений седловые точки на поверхности ошибки на самом деле представляют собой более серьезную проблему, чем локальные минимумы.

Заключение

Надеюсь, вам понравилось обсуждение локальных минимумов. В следующей статье мы обсудим некоторые методы, которые помогают нейронной сети достичь глобального минимума (если мы действительно этого хотим).