Double-Gated Nanohelix как новая настраиваемая двоичная сверхрешетка
Аннотация
Мы теоретически исследуем проблему электрона, заключенного в наноспираль между двумя параллельными затворами, смоделированными как заряженные провода. Система наноспиралей с двойным затвором представляет собой бинарную сверхрешетку со свойствами, очень чувствительными к напряжениям затвора. В частности, зонная структура демонстрирует пересечения энергетических зон для определенных комбинаций напряжений затвора, что может привести к квазирелятивистским явлениям, подобным дираковским. Наш анализ оптических переходов, индуцированных линейно и циркулярно поляризованным светом, показывает, что наноспираль с двойным закрытием может использоваться для различных оптоэлектронных приложений.
Введение
От окаменелых спиралевидных брюхоногих моллюсков, которых первый автор с энтузиазмом собирал в детстве, до переплетенной структуры ДНК, которая, несомненно, когда-то определяла этих доисторических существ, геометрия спирали преобладает во всей природе [1]. Вдохновленные сложными функциональными возможностями, приписываемыми формам встречающихся в природе биомолекул [2–6], ожидается, что другие системы, обладающие спиральной геометрией, подходящей для нанотехнологий, дадут богатую физику и внесут свой вклад в новые приложения. За последние три десятилетия значительный прогресс в технологиях нанопроизводства привел к реализации наноспиралей в большом количестве различных систем, включая InGaAs / GaAs [7], Si / SiGe [8], ZnO [9–11], CdS [ 12], SiO 2 / SiC [13,14] и чистый углерод [15–20], а также полупроводники II – VI и III – V [21] (современное состояние дел см. В [21–26]). Следовательно, в таких структурах ожидается множество явлений, начиная от экзотических транспортных свойств, таких как топологическая квантованная накачка заряда [27, 28], сверхпроводимость [29] и спиновая фильтрация [30–32], до молекулярной и наномеханической растягиваемой электроники [33, 34] из-за пьезоэлектрических эффектов [35], сенсорных приложений [36, 37], энергии [38] и накопления водорода [39], а также полевых транзисторов [40, 41].
Очарование устройств на основе наноспиралей в конечном итоге связано с присущей им периодичностью, закодированной в топологии спиральной структуры. В частности, воздействие на наноспираль поперечным электрическим полем (перпендикулярным оси спирали) вызывает поведение сверхрешетки, такое как брэгговское рассеяние электронов на суперпериодическом потенциале, приводящее к расщеплению энергии на краю зоны Бриллюэна сверхрешетки между низшие состояния, линейно перестраиваемые электрическим полем [42, 43]. Такое поведение может приводить к блоховским осцилляциям и отрицательной дифференциальной проводимости [44, 45] и может подчеркивать спин-поляризованный перенос через спирали [31, 46], а также приводить к усилению кругового дихроизма, полезному в нанофотонных хироптических приложениях [47]. Эта система представляет собой унарную сверхрешетку и, кроме того, открывает возможность использования наноспиралей в качестве туннельных диодов или диодов Ганна для умножения частоты, усиления и генерации или поглощения излучения в превознесенном терагерцовом диапазоне [48–51]. В то время как прототипная сверхрешетка обычно реализуется в гетероструктурах из чередующихся полупроводниковых слоев с различной собственной шириной запрещенной зоны, параметры сверхрешетки наноспирали полностью контролируются внешним полем. Напротив, формы бывших обычных сверхрешеточных потенциалов специфичны для гетероструктуры и, будучи устойчивыми, предлагают ограниченные возможности для манипулирования в ходе ее эксплуатации без использования больших внешних полей. Следовательно, привлекательность использования наноспиралей в качестве сверхрешеток вместо этого заключается в их большей настраиваемости.
С другой стороны, с гетероструктурными полупроводниковыми сверхрешетками (или действительно фотонными сверхрешеточными структурами [52–55] и холодными атомами в оптических решетках [56, 57]) можно создавать более сложные элементарные ячейки сверхрешетки за пределами простой квантовой ямы, которая индуцируется электрическое поле вдоль спирали. Даже расширение до бинарной сверхрешетки [58–60] (при этом элементарная ячейка отличается двумя разными квантовыми ямами и / или барьерами) обещает богатый набор физики, такой как осцилляции Блоха-Зинера [61], которые, в свою очередь, могут способствовать для перестраиваемых светоделителей и интерферометров [62]. Таким образом, было бы весьма желательно объединить настраиваемость внешнего поля сверхрешетки на основе наноспиралей с превосходной функциональностью бинарной сверхрешетки.
Ниже мы описываем именно такую систему с наноспиралью, расположенной между двумя параллельно закрытыми заряженными проволоками, выровненными по оси спирали. Мы предполагаем применение дополнительного поперечного электрического поля и теоретически показываем, что потенциал, управляемый затвором и полем, образует двойную сверхрешетку вдоль одномерной спирали.
Методы
Теоретическая модель
Начнем с изучения случая одноэлектронной полупроводниковой круговой наноспирали с N витки радиусом R , шаг p , и общая длина L = Np . Наноструктура расположена между двумя параллельными воротами, смоделированными как заряженные проволоки с осью спирали, выровненной вдоль z -оси с осью и затворами, находящимися в одной плоскости, как показано на рис. 1. Кроме того, мы рассматриваем внешнее поперечное электрическое поле, нормальное к плоскости оси затвора \ (\ mathbf {E} =E _ {\ bot} \ hat {\ mathbf {y}} \), который можно использовать для нарушения симметрии отражения потенциала над плоскостью по отношению к потенциалу под плоскостью. Мы работаем в винтовых координатах, параметрически описываемых с помощью r . =( x, y , z ) =( R cos ( s φ ), R грех ( s φ ), ρ φ ), где динамическая угловая координата φ = z / ρ зависит только от расстояния по оси спирали с ρ = p / 2 π , и s =± 1 указывает на левую или правую спираль соответственно. В данной работе мы рассматриваем левостороннюю спираль s =1. В рамках модели эффективной массы энергетический спектр ε ν из ν Собственное состояние электрона в спирали под действием таких внешних потенциалов находится из уравнения Шредингера:
$$ - \ thinspace \ frac {\ hbar ^ {2}} {2M ^ {*} \ rho ^ {2}} \ frac {d ^ {2}} {d \ varphi ^ {2}} \ psi _ {\ nu} + \ left [V_ {g} (\ varphi) + V _ {\ bot} (\ varphi) \ right] \ psi _ {\ nu} =\ varepsilon _ {\ nu} \ psi _ {\ nu} $$ (1 )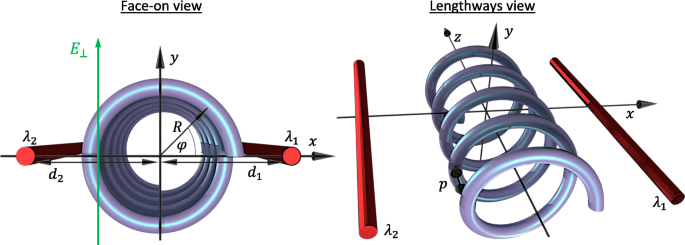
Диаграмма геометрии и параметров системы с фронтальной и продольной точек зрения. R - радиус спирали, а d 1 и d 2 - расстояния заряженных проводов от оси спирали с плотностями заряда λ 1 и λ 2 , соответственно. Пространственная координата φ описывает угловое положение на спирали спереди и относится к z -координат через φ =2 π г / p с p шаг спирали. Поперечное электрическое поле E ⊥ применяется параллельно y -ось
где мы геометрически перенормировали эффективную массу электрона M e до M ∗ = M e (1+ R 2 / ρ 2 ), чтобы выразить все через координату вдоль оси спирали (напомним, что φ = z / ρ ), что более удобно для внешних потенциалов. Здесь V ⊥ ( φ ) =- eE ⊥ R грех ( φ ) - вклад поперечного электрического поля, направленного вдоль y -ось такая, что V ⊥ ( π / 2) <0. Потенциал от ворот V г ( φ ) =- e [ Φ 1 ( φ ) + Φ 2 ( φ )] с электростатическим потенциалом, ощущаемым электроном вдоль спирали из-за отдельного заряженного провода, определяемого как Φ я ( φ ) =- λ я к ln ( r я / d я ). Здесь я =1,2 обозначает провода, λ я - линейная плотность заряда на проводе, а \ (k =1/2 \ pi \ tilde {\ epsilon} \) с \ (\ tilde {\ epsilon} \) - абсолютная диэлектрическая проницаемость. Перпендикулярное расстояние между испытательным зарядом и конкретным проводом равно \ (r_ {i} =[d ^ {2} _ {i} + R ^ {2} + 2 (-1) ^ {i} d_ {i } R \ cos (\ varphi)] ^ {1/2} \), с d я обозначающее соответствующее расстояние проволоки до оси спирали. Мы определили, что нулевой потенциал, индуцированный затвором, находится вдоль оси спирали. Полный одномерный потенциал V Т ( φ ) = V г ( φ ) + V ⊥ ( φ ) явно периодический V Т ( φ ) = V Т ( φ +2 π нет ) с периодом 2 π в целом (что соответствует периоду p по координате z ). Этот период значительно превышает межатомное расстояние и приводит к типичным сверхрешеточным эффектам. Эта буква отличается от наноспирали поперечным электрическим полем (которое можно воспроизвести с помощью V Т ( φ ) = V ⊥ ( φ ) здесь) главным образом путем манипулирования повторяющейся элементарной ячейкой сверхрешетки через потенциал двойного затвора V г ( φ ). Принимая предел p → 0, мы возвращаемся к частице на картинке кольца с двумя электростатическими затворами [63, 64]. Делаем приближение R / d я ≪1, мы можем расширить V г ( φ ) до второго порядка по cos ( φ ), и при преобразовании уравнения. 1 в безразмерном виде мы приходим к
$$ {\ begin {align} \ frac {d ^ {2} \ psi _ {\ nu}} {d \ varphi ^ {2}} + \ left [\ epsilon _ {\ nu} + 2A_ {g} \ cos ( \ varphi) + 2B_ {g} \ cos (2 \ varphi) + 2C _ {\ bot} \ sin (\ varphi) \ right] \ psi _ {\ nu} =0, \ end {align}} $$ (2)с величинами в единицах шкалы энергии \ (\ varepsilon _ {0} (\ rho) =\ hbar ^ {2} / 2 M ^ {*} \ rho ^ {2} \), определяемыми как
$$ \ begin {array} {@ {} rcl @ {}} A_ {g} &=&\ beta \ frac {\ left (d_ {1} ^ {2} + R ^ {2} \ right)} { d_ {1} R} (1- \ gamma), \ qquad B_ {g} =\ frac {\ beta} {2} \ left (1+ \ frac {\ lambda_ {1}} {\ lambda_ {2}} \ gamma ^ {2} \ right), \\ C _ {\ bot} &=&e E _ {\ bot} R / 2 \ varepsilon_ {0} (\ rho), \ qquad \ qquad \ qquad \; \ epsilon _ {\ nu} =\ frac {\ varepsilon _ {\ nu}} {\ varepsilon_ {0} (\ rho)}. \ конец {массив} $$ (3)Здесь \ (\ beta =ek d_ {1} ^ {2} R ^ {2} \ lambda _ {1} / 2 \ left (d_ {1} ^ {2} + R ^ {2} \ right) ^ {2} \ varepsilon _ {0} (\ rho) \) характеризует вклад гейта 1, в то время как параметр асимметрии \ (\ gamma =\ lambda _ {2} d_ {2} \ left (d_ {1} ^ {2 } + R ^ {2} \ right) / \ lambda _ {1} d_ {1} \ left (d_ {2} ^ {2} + R ^ {2} \ right) \) характеризует относительный вклад гейта 2 , с γ =1, что соответствует равным вкладам затвора в потенциал (в результате получается A г =0). Следует отметить, что неизбежная асимметрия, вызванная сложностью поддержания d 1 = d 2 можно компенсировать, манипулируя λ 1 и λ 2 . В этом письме мы ограничимся рассмотрением γ ≤1 (что равно | Φ 1 |> | Φ 2 |), поскольку параметр асимметрии, превышающий единицу, может быть отображен в эквивалентную систему ниже единицы посредством простого обмена индексами, обозначающими ворота, и соответствующего сдвига в перспективе φ → φ ± π . Мы также будем рассматривать только C ⊥ ≥0 из-за симметрии отрицательного C ⊥ относительно такого переноса координат в φ , и A г ≥0, B г > 0 (т.е. только положительные плотности заряда на проводах β > 0), поскольку любой потенциальный ландшафт с отрицательно заряженными воротами может быть воспроизведен с правильной комбинацией параметров положительно заряженных ворот. На рис. 2 нанесен безразмерный потенциал V . Т ( φ ) / ε 0 ( ρ ), с силой π -периодическая составляющая потенциала, фиксированная на B г =0,2, для нескольких комбинаций параметров возмущения с удвоенным периодом A г и C ⊥ . Мы видим, что полный внешний потенциал индуцирует двойную сверхрешетку вдоль φ , с двойной квантовой ямой (ДКЯ) в качестве элементарной ячейки, выделенной синим цветом. Это может принимать качественно разные формы, манипулируя относительными вкладами ворот γ и поперечное электрическое поле E ⊥ . Элементарная ячейка по существу представляет собой одиночную яму при эквивалентных затворах ( γ =1) и отсутствие поперечного электрического поля E ⊥ =0 (как на рис. 2а для A г = C ⊥ =0). Исправление E ⊥ =0, с более сильным вкладом гейта 1 ( γ <1), элементарная ячейка становится ДКЯ с разными минимумами ямы и вырожденными максимумами барьеров (рис. 2b, где A г =0,1 и C ⊥ =0). Напротив, поддержание вырожденных минимумов DQW и манипулирование двумя потенциальными барьерами по отношению друг к другу требует симметричных вкладов затвора ( γ =1) в ненулевом электрическом поле E ⊥ ≠ 0 (рис. 2c с A г =0 и C ⊥ =0,1). Объединение вкладов асимметричных вентилей ( γ <1) с E ⊥ 0 дает DQW с разными минимумами потенциальной ямы и разными барьерами (как видно на рис. 2d, где оба A г = C ⊥ =0,1). Это приводит к качественно иному и разнообразному поведению, как мы увидим в следующих разделах.
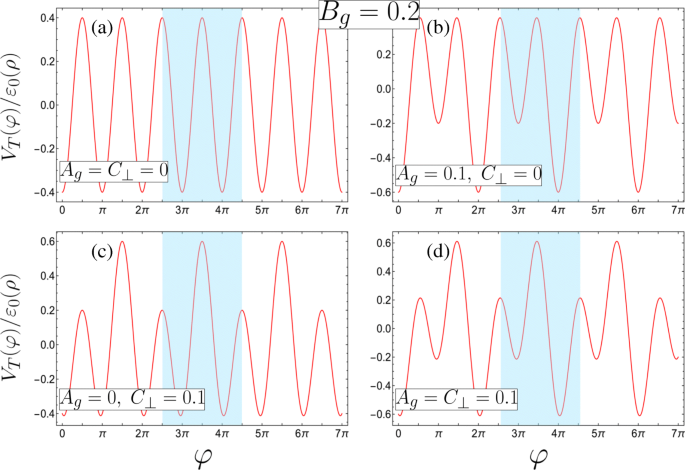
Четыре возможных конфигурации потенциала сверхрешетки с элементарными ячейками, выделенными синим цветом (определенные в терминах безразмерных параметров, см. Уравнение 3 для соответствующих требований к физическим параметрам, и все с B г =0,2). а Унарная сверхрешетка с вырожденными минимумами и максимумами в элементарной ячейке ( A г = C ⊥ =0). б - г Бинарные сверхрешетки, образованные из b асимметричная ДКЯ с разными минимумами и симметрией внутреннего отражения относительно любого минимума из-за вырожденных максимумов ( A г =0,1, C ⊥ =0), c симметричная ДКЯ только с вырожденными минимумами ( A г =0, C ⊥ =0,1) или d асимметричный DQW с разными минимумами и максимумами ( A г = C ⊥ =0,1)
Решения в виде бесконечной матрицы
Решения уравнения. 2 можно найти в терминах функций Блоха
$$ \ psi_ {n, q} (\ varphi) =(2 \ pi N \ rho) ^ {- \ frac {1} {2}} e ^ {iq \ varphi} \ sum_ {m} c ^ {( n)} _ {m, q} e ^ {im \ varphi}, $$ (4)где q = k z ρ - безразмерная форма квазиимпульса электрона k z по оси спирали, n указывает поддиапазон, а префактор возникает в результате нормализации в терминах φ :\ (\ rho \ int _ {0} ^ {2 \ pi N} | \ psi _ {n, q} (\ varphi) | ^ {2} d \ varphi =1 \). Мы используем ортогональность экспоненциальных функций, умножая полученное выражение на \ (e ^ {im ^ {\ prime} \ varphi} / 2 \ pi \) и интегрируя по φ , где м ′ является целым числом, так что мы приходим к бесконечному множеству одновременных уравнений для коэффициентов \ (c ^ {(n)} _ {m, q} \),
$$ {\ begin {align} &\ left [(q + m) ^ {2} - \ epsilon_ {n} \ right] c ^ {(n)} _ {m} - \ left (A_ {g} - i C _ {\ bot} \ right) c ^ {(n)} _ {m-1} - \ left (A_ {g} + i C _ {\ bot} \ right) c ^ {(n)} _ {m +1} \\ &\ quad- B_ {g} \ left (c ^ {(n)} _ {m + 2} + c ^ {(n)} _ {m-2} \ right) =0, \ конец {выровнен}} $$ (5)где для наглядности q -подстрочные обозначения были опущены, ε n, q ≡ ε n и \ (c_ {m} ^ {(n)} \ Equiv c_ {m, q} ^ {(n)} \). Уравнение 5 представляет собой бесконечную пятидиагональную матрицу, в которой очевидно, что система периодична по q , и мы можем ограничиться рассмотрением первой зоны Бриллюэна, определенной как - 1 / 2≤ q ≤1 / 2. В отсутствие потенциала сверхрешетки A г = B г = C ⊥ =0, собственные значения затем нумеруются m задано ε м =( м + д ) 2 и мы узнаем м быть квантовым числом углового момента, связанным со свободным электроном на спирали. Мы видим из уравнения. 5 что когда A г = C ⊥ =0 только состояния с Δ м =± 2 смешаны, в то время как формирование элементарной ячейки ДКЯ с разными минимумами скважин или барьерами достигается с помощью A г ≠ 0 и / или C ⊥ ≠ 0, также смешивает состояния с Δ м =± 1. Интересно, что система электрона на спирали под действием внешнего поперечного потенциала (который изменяется на один оборот спирали) математически эквивалентна электрону на квантовом кольце, пронизанном магнитным полем и подверженном воздействию потенциала с одна и та же функциональная форма, изменяющаяся по угловой координате; например см. Ref. [65–67] или сравните, например, ссылки. [42–45] с [68–70]. Для кольца роль играет q здесь поглощается магнитным потоком. Следовательно, точно такой же анализ в этой работе применим к проблеме квантового кольца с двойным затвором [63–66], если кольцо должно быть пронизано магнитным потоком.
Усечение и численная диагонализация матрицы, соответствующей уравнению. 5 предоставляет n собственные энергии поддиапазона ε n и коэффициенты \ (c_ {m} ^ {(n)} \) для каждого значения q . Применяем усечение на | m | =10, можно быть уверенным в том, что любое увеличение размера матрицы не приводит к заметным изменениям в самых нижних поддиапазонах.
Результаты и обсуждение
Структура полос наноспирали с двойным закрытием
На рис. 3 изображена энергетическая дисперсия самых нижних полос для нескольких комбинаций параметров. В зависимости от формы сверхрешетки мы обнаруживаем заметное разнообразие в поведении дисперсии, и для некоторых конкретных комбинаций параметров мы обнаруживаем пересечения энергетических зон для определенных подзон либо на краю зоны Бриллюэна (рис. 3a и c), либо на границе центр зоны Бриллюэна (рис. 3б и г).
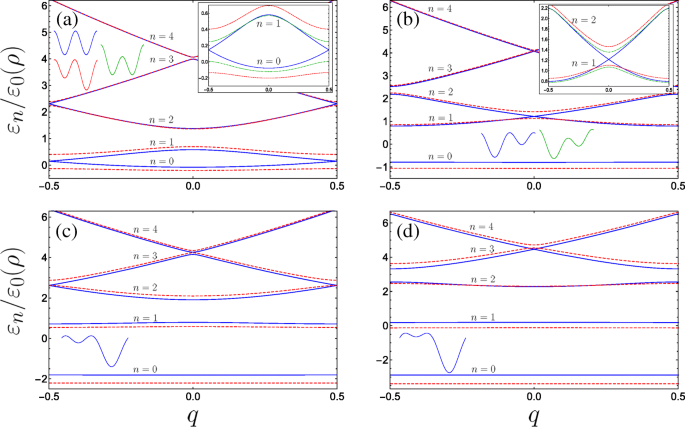
Ленточная структура для системы наноспиралей с двойным затвором для различных комбинаций безразмерных параметров (с B г =0,4, фиксировано повсюду): a Сплошной синий (красный пунктир) графики A г =0 & C ⊥ =0 ( A г =0,2 & C ⊥ =0), на вставке дополнительно показано поведение двух нижних подзон под действием поперечного электрического поля с A г =0 & C ⊥ =0,2 как пунктирная зеленая кривая. б Сплошной синий (красный пунктир) графики A г =0,63 & C ⊥ =0 ( A г =0,8 & C ⊥ =0), где синяя кривая изображает первый резонанс (см. Текст) с энергетическими полосами, пересекающимися в центре зоны Бриллюэна, на вставке сравнивается поведение двух нижних возбужденных подзон со случаем, когда A г =0,63 & C ⊥ =0,2 как пунктирная зеленая кривая. c Сплошной синий (красный пунктир) графики A г =1,26 & C ⊥ =0 ( A г =1,5 & C ⊥ =0), где синяя кривая изображает второй резонанс с закрытием энергетических щелей на краю Бриллюэна для более высоких полос. г Мини-щели третьего резонанса и более высоких поддиапазонов закрываются в центре, причем сплошной синий (красный пунктир) означает A г =1.9 & C ⊥ =0 ( A г =2.2 & C ⊥ =0). Набросаны формы элементарной ячейки, n перечисляет бэнды, а оси врезок совпадают с осями основных графиков
Малое возмущение с удвоенным периодом поля
Когда A г = C ⊥ =0 элементарная ячейка представляет собой две эквивалентные квантовые ямы, и, следовательно, появление пар полос, соприкасающихся на краях зоны Бриллюэна, возникает естественным образом. Действительно, если взять только одну скважину в качестве элементарной ячейки, период сверхрешетки уменьшается вдвое и зона Бриллюэна удваивается - 1≤ q ≤1. Затем мы наблюдали бы обычную зонную диаграмму унарной сверхрешетки, в которой запрещенная зона между основной и первой зонами при q =1 задается здесь через запрещенную зону между n =1 и n =2 при q =0 и будет линейным в B г из теории возмущений. Тем не менее, мы представляем описание ленточной структуры на | q | =1/2 в изображении элементарной ячейки ДКЯ с использованием матричной алгебры в Приложении. Как видно на вставке к рис. 3а, введение любого из двухпериодных потенциальных членов открывает запрещенную зону на краю зоны Бриллюэна. Элементарная ячейка из вкладов симметричного затвора ( A г =0) сохраняет форму симметричной ДКЯ при приложении поперечного поля C ⊥ перпендикулярно оси спираль-затвор, причем один потенциальный барьер модифицирован относительно другого (обозначен зеленым эскизом DQW на рис. 3a). Пока C ⊥ открывает запрещенную зону, изменение дисперсии заметно менее чувствительно, чем изменение от аналогичной величины приложенного A г . Это видно по меньшей ширине запрещенной зоны при | q | =1/2 для пунктирной зеленой линии на вставке рис. 3a (с A г =0 и C ⊥ =0,2) по сравнению с большим промежутком для красной пунктирной кривой (которая соответствует A г =0,2 и C ⊥ =0). Чтобы подчеркнуть это поведение, на рис. 4а показан размер запрещенной зоны при | q | =1/2 между двумя нижними поддиапазонами \ (\ Delta \ varepsilon _ {01} ^ {(q =1/2)} / \ varepsilon _ {0} (\ rho) \) для фиксированного B г =0,25 как функция от C ⊥ (с A г =0) и A г (с C ⊥ =0) в виде штрихпунктирных зеленых и красных штриховых кривых соответственно. В нулевом поперечном электрическом поле и асимметричных потенциалах затвора ( C ⊥ =0 и A г 0), то элементарная ячейка представляет собой асимметричную ДКЯ, хотя и с симметрией внутреннего отражения относительно минимумов любой скважины из-за эквивалентных барьеров. Тогда мы сможем понять более высокую чувствительность запрещенной зоны к изменению A г рассмотрев свойства изолированной элементарной ячейки ДКЯ, из которой построена сверхрешетка. С A г = C ⊥ =0, при | q | =1/2 (края зоны Бриллюэна), блоховские состояния, образованные из основного и первого возбужденного состояния изолированной элементарной ячейки ДКЯ (см. Синюю схему и сопровождающие волновые функции на рис. 4а), будут различаться только на произвольная фаза. Эта ситуация соответствует бесщелевой голубой дисперсионной кривой на рис. 3а. Как схематично изображено на рис. 4a зеленым эскизом DQW, C ⊥ уменьшает относительные максимумы одного из барьеров относительно другого, при этом минимумы ДКЯ остаются вырожденными. Таким образом, основное состояние изолированной ДКЯ модифицируется только за счет небольшого увеличения его распределения вероятностей под меньшим потенциальным барьером (что дает лишь небольшое снижение энергии по сравнению с невозмущенным основным состоянием), а первое возбужденное состояние остается практически неизменным. поскольку его узел расположен под барьером и не чувствителен к его изменению. Состояния Блоха на краю зоны Бриллюэна, которые построены из этих основного и первого возбужденных состояний, отличаются от невозмущенного случая только уменьшенным затуханием волновой функции основного состояния под меньшим барьером (сравните зеленую ДКЯ с синей ДКЯ на рис. Рис. 4а). Изменение A г манипулирует относительными положениями минимумов DQW, сохраняя при этом вырожденные барьеры. Волновые функции двух нижних изолированных состояний ДКЯ значительно различаются:основное состояние стремится к локализованному основному состоянию особой более глубокой ямы, а первое возбужденное состояние стремится к локализованному основному состоянию более мелкой ямы [71]. В то время как возмущение снижает энергию основного состояния, энергия первого возбужденного состояния сравнительно увеличивается, поскольку минимумы более мелкой ямы смещаются вверх с увеличением A г , что приводит к более высокой чувствительности размера запрещенной зоны по отношению к A г . В частности, частица в основной подзоне быстро оказывается удерживаемой около дна самой глубокой потенциальной ямы с увеличением A г . Таким образом, нижняя полоса приближается к плоской полосе без дисперсии быстрее, чем в случае поперечного поля, что может привести к электронной нестабильности и эффектам сильного взаимодействия, сопровождающим высокую плотность состояний [72].
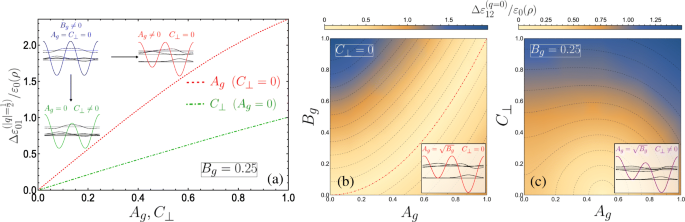
а Размер запрещенной зоны между землей и первым поддиапазоном как функция от A г ( C ⊥ ) отображается красным пунктиром (пунктирно-зеленым), здесь B г =0,25. Диаграммы показывают влияние различных возмущений на изолированную элементарную ячейку ДКЯ и собственные состояния. б - c Размер запрещенной зоны между первым и вторым поддиапазонами, указанный на двумерном графике плотности, как функция от; б А г и B г для C ⊥ =0 и c А г и C ⊥ с фиксированным B г =0,25. б Соседние изоэнергетические изолинии показывают разницу в 0,17, с нулевым зазором, обозначенным пунктирной красной линией для \ (A_ {g} =\ sqrt {B_ {g}} \), тогда как c разница составляет 0,13 с нулевым зазором в центре наименьшего контура полукруга (0,5,0). На диаграммах изображены изолированные DQW и собственные состояния. Гибридизации не происходит между s -лайк и p -подобные резонансные локализованные состояния отдельных ям в b , но в c из-за электрического поля, изменяющего один барьер относительно другого
Пересечение энергетических диапазонов
Примечательно, что если мы сохраним C ⊥ =0 и увеличьте A г , в то время как первоначально все вырождения снимаются, последующие более высокие энергетические полосы пересекают друг друга, чередуя центр и край зоны Бриллюэна (наблюдайте за поведением чередующихся синих и пунктирных красных кривых, переходящих от рис. 3a к d). Физически мы можем понять исчезающую запрещенную зону с точки зрения взаимодействия локализованных волновых функций в элементарной ячейке. Когда асимметричный потенциал DQW таков, что основное состояние в более мелкой яме ( s -подобная орбиталь) резонирует с первым возбужденным состоянием в более глубокой яме ( p -подобно орбитальной), в точке q =0 из-за симметрии отражения относительно центра любой из ям, противоположные четности этих состояний предотвращают обычную туннельную связь между ними, и, следовательно, возбужденные состояния, построенные из этих орбиталей, совпадают (синие кривые на рис. 3b). Это напоминает так называемые s - p резонансы в оптических решетках [73, 74]. Точно так же, если параметры таковы, что локализованное основное состояние в мелкой яме резонирует с возбужденным состоянием в более глубокой яме, имеющим ту же четность, то при | q | =1/2, присутствие фазы Блоха полностью подавляет обычную гибридизацию между этими двумя соседними локализованными состояниями ямы, и запрещенная зона закрывается (как показано на рис. 3c для резонанса основного состояния со вторым возбужденным состоянием). На языке рассеяния на периодическом потенциале; запрещенная зона закрывается из-за полной деструктивной интерференции амплитуд брэгговского рассеяния второго порядка от cos ( φ ) потенциала и амплитуды рассеяния первого порядка от cos (2 φ ) потенциал [75–77].
Мы можем количественно показать существование пересечений энергетических зон (при нулевом поперечном электрическом поле) как в центре, так и на краю зоны Бриллюэна, вернувшись к формуле. 2, которое можно распознать как уравнение Уиттекера-Хилла, когда C ⊥ =0 [78]. Функции Блоха Ур. 4 подчиняются закрученным периодическим граничным условиям ψ n, q ( φ +2 π ) =ехр (2 π iq ) ψ n, q ( φ ). В частности, когда q =0 формальные решения уравнения. 2 равны 2 π -периодический, тогда как когда | q | =1/2 решения равны 2 π -антипериодический (поэтому будем искать 4 π -периодические решения). В частности, уравнение. 2 с C ⊥ =0 может быть отображено в уравнение Инса [79, 80], которое является квазиточно решаемым, путем выражения волновой функции как произведения асимптотического решения уравнения 2 и неизвестная функция \ (\ psi _ {n, q} (\ varphi) =\ exp \ left [-2 \ sqrt {B_ {g}} \ cos (\ varphi) \ right] \ Phi _ {n, q} (\ varphi) \), такой что
$$ \ frac {d ^ {2} \ Phi_ {n, q}} {d \ varphi ^ {2}} + \ frac {\ xi} {2} \ sin (\ varphi) \ frac {d \ Phi_ { n, q}} {d \ varphi} + \ frac {1} {4} \ left [\ eta_ {n, q} - p \ xi \ cos (\ varphi) \ right] \ Phi_ {n, q} =0, $$ (6)где мы определили вспомогательные параметры \ (\ xi =8 \ sqrt {B_ {g}} \), η n, q =4 ε n, q +8 B г , \ (- p \ xi =8A_ {g} +8 \ sqrt {B_ {g}} \) и Φ n, q ( φ ) поддерживает необходимую скрученную периодичность каждого решения (обратите внимание, что здесь p не нет шаг спирали). Кроме того, поскольку потенциал сверхрешетки здесь инвариантен относительно преобразования φ → - φ , решения для q =0 и q =1/2 можно разделить на четность и нечетность, так что следующие тригонометрические ряды
$$ \ Phi_ {n, 0} ^ {(e)} (\ varphi) =\ sum_ {l =0} a ^ {(n)} _ {l} \ cos (l \ varphi), $$ (7a ) $$ \ Phi_ {n, 0} ^ {(o)} (\ varphi) =\ sum_ {l =0} b ^ {(n)} _ {l + 1} \ sin [(l + 1) \ varphi], $$ (7b) $$ \ Phi_ {n, \ frac {1} {2}} ^ {(e)} (\ varphi) =\ sum_ {l =0} \ widetilde {a} ^ {( n)} _ {l} \ cos \ left [\ left (l + \ frac {1} {2} \ right) \ varphi \ right], $$ (7c) $$ \ Phi_ {n, \ frac {1} {2}} ^ {(o)} (\ varphi) =\ sum_ {l =0} \ widetilde {b} ^ {(n)} _ {l + 1} \ sin \ left [\ left (l + \ frac {1} {2} \ right) \ varphi \ right], $$ (7d)покрывают формальные решения, и отметим, что решения для q =−1 / 2 такие же, как для q =1/2. Здесь верхние индексы e и o пометьте функции как четные и нечетные соответственно и n по-прежнему относится к n -й поддиапазон, который также является n -ое собственное состояние для указанных q ценности. Подставляя их в формулу. 6 приводит к трехчленным рекурсивным соотношениям для коэффициентов Фурье. q =0 дает четное решение
$$ - \ eta_ {n, 0} ^ {(e)} a ^ {(n)} _ {0} + \ xi \ left (\ frac {p} {2} +1 \ right) a ^ {( n)} _ {2} =0, $$ (8a) $$ \ xi pa ^ {(n)} _ {0} + \ left (4 - \ eta_ {n, 0} ^ {(e)} \ справа) a ^ {(n)} _ {2} + \ xi \ left (\ frac {p} {2} +2 \ right) a ^ {(n)} _ {4} =0, $$ (8b ) $$ {\ begin {align} &\ xi \ left (\ frac {p} {2} - l +1 \ right) a ^ {(n)} _ {2l-2} + \ left (4l ^ { 2} - \ eta_ {n, 0} ^ {(e)} \ right) a ^ {(n)} _ {2l} \\ &\ quad + \ xi \ left (\ frac {p} {2} + l +1 \ right) a ^ {(n)} _ {2l + 2} =0, \ qquad (l \ ge 2) \ end {align}} $$ (8c)и соответствующие рекурсивные соотношения для нечетного решения для q =0
$$ (4 - \ eta_ {n, 0} ^ {(o)}) b ^ {(n)} _ {2} + \ xi \ left (\ frac {p} {2} +2 \ right) b ^ {(n)} _ {4} =0, $$ (9a) $$ {\ begin {выровнено} &\ xi \ left (\ frac {p} {2} - l +1 \ right) b ^ { (n)} _ {2l-2} + \ left (4l ^ {2} - \ eta_ {n, 0} ^ {(o)} \ right) b ^ {(n)} _ {2l} + \ xi \ left (\ frac {p} {2} + l +1 \ right) b ^ {(n)} _ {2l + 2} \\ &=0. \ qquad (l \ ge 2) \ end {выровнено} } $$ (9b)q =1/2 четное решение дает
$$ \ left [1 - \ eta_ {n, \ frac {1} {2}} ^ {(e)} + \ frac {\ xi} {2} (p + 1) \ right] \ widetilde {a} ^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{a}^{(n)}_{3}=0, $$ (10a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l +1)\widetilde{a}^{(n)}_{2l-1}+\left[(2l+1 )^{2} - \eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{a}^{(n)}_{2l+1}\\ &\ quad+ \frac{\xi}{2}(p+2l+3)\widetilde{a}^{(n)}_{2l+3}=0, \qquad (l \ge 1) \end{aligned} } $$ (10b)and the q =1/2 odd solution gives
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} -\frac{\xi}{2}(p+1) \right]\widetilde{b}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{b}^{(n)}_{3}=0 $$ (11a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l+1)\widetilde{b}^{(n)}_{2l-1}+\left[(2l+1)^{2} -\eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{b}^{(n)}_{2l+1}\\&\quad + \frac{\xi}{2}(p+2l+3)\widetilde{b}^{(n)}_{2l+3}=0. \qquad (l \ge 1) \end{aligned}} $$ (11b)Consider then Eqs. (8c) and (9b) for the q =0 solutions. The series solutions (7a) and (7b) can clearly be made to terminate if p is 0 or an even positive integer. The resulting polynomials are referred to as Ince polynomials. The remaining solutions for higher eigenvalues are simultaneously double degenerate and correspond to the energy crossings observed at q =0 for certain parameters. The existence of these degeneracies can be seen by looking at the diagonalizable matrices describing the recursion relations for a l и b l :
$$ \boldsymbol{\mathcal{A}} =\left[ \begin{array}{ccccc} 0 &\xi\left(\frac{p}{2} +1 \right) &0 &0 &\hdots \\ \xi p &4 &\xi\left(\frac{p}{2} +2 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \end{array} \right]\!, $$ (12)and
$$ \boldsymbol{\mathcal{B}} =\left[ \begin{array}{ccccc} 4 &\xi\left(\frac{p}{2} +2 \right) &0 &0 &\hdots \\ \xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} -2 \right) &36 &\xi\left(\frac{p}{2} +4 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \\ \end{array} \right]\! $$ (13)соответственно. Either of the above tridiagonal matrices can be broken into tridiagonal sub-matrices if a leading off-diagonal matrix element is equal to zero, i.e. if p is an even number. The matrices will decompose into two tridiagonal blocks, one smaller finite matrix \(\boldsymbol {\mathcal {A}_{1}}\) (\(\boldsymbol {\mathcal {B}_{1}}\)) and a remaining infinite matrix \(\boldsymbol {\mathcal {A}_{2}}\) (\(\boldsymbol {\mathcal {B}_{2}}\)). From the theory of tridiagonal matrices the corresponding eigenvalue spectra for each matrix is then \(\eta (\boldsymbol {\mathcal {A}}) =\eta (\boldsymbol {\mathcal {A}_{1}}) \cup \eta (\boldsymbol {\mathcal {A}_{2}})\) and \(\eta (\boldsymbol {\mathcal {B}}) =\eta (\boldsymbol {\mathcal {B}_{1}}) \cup \eta (\boldsymbol {\mathcal {B}_{2}})\). The smaller finite matrices are analytically diagonalizable in principle, giving exact eigenvalues, and their corresponding finite length eigenvectors define the fourier coefficients yielding Ince polynomials via Eq. 7. We can see that for a given even integer p , the remaining infinite tridiagonal matrices are the same \(\boldsymbol {\mathcal {A}_{2}}=\boldsymbol {\mathcal {B}_{2}}\equiv \boldsymbol {\mathcal {D}}\) which results in the double degenerate eigenvalues. To be clear, we provide an example of when p =2 in the Appendix.
In the same way, when p is a positive odd integer the series solutions (7c) and (7d) can be made to terminate, and the matrices corresponding to \(\widetilde {a}_{l}\) and \(\widetilde {b}_{l}\) share eigenvalues resulting in the closing of higher subbands at the edge of the Brillouin zone q =± 1/2. From the definitions of the auxiliary parameters in Eq. 6, we have
$$ A_{g} =(p+1)\sqrt{B_{g}}, $$ (14)which defines the condition for exactly-solvable solutions for the lower lying solutions and simultaneously the existence of higher double degenerate eigenvalues above the p th subband, with p =0 or an even positive integer corresponding to crossings at the centre of the Brillouin zone, while crossings at the edge require p to be an odd positive integer. Figure 4b plots the size of the band gap between the first and second subbands \(\Delta \varepsilon _{12}^{(q=0)}/\varepsilon _{0}(\rho)\) as a function of A г и B г , with the dot-dashed red contour line corresponding to Eq. 14 for p =0. The schematic indicates the appropriate eigenstates of the isolated DQW at the p =0 resonance.
The application of a small transverse field C ⊥ breaks the reflection symmetry of the system, permitting hybridization of the localized well states of the isolated DQW which results in a significant change at points of degeneracy, as can be seen by comparing the schematic depicted in Fig. 4b with that in c (see also inset of Fig. 3b). We plot in Fig. 4c the behaviour of the band gap between the first and second subbands as a function of A г и C ⊥ . Here we see that the band gap is more sensitive to C ⊥ due to the significant change in the isolated DQW eigenstates by lowering one barrier with respect to the other. This behaviour is notably the converse of the parameter sensitivity for the band gap between the ground and first subbands. By degenerate perturbation theory, it can be shown that this induced band gap is linear in C ⊥ for the lowest crossing bands when p =0, and to higher order with increasing p . Finally, within the vicinity of the crossings, e.g. for small q about q =0 in Fig. 3a, the dispersions could be approximated as a quasi-relativistic linear dispersion yielding Dirac-like physics, which could permit superfluiditiy [81] for example. The advantage in using nanohelices lies in introducing such phenomena to portable nanostructure based devices, while also exhibiting unusual responses of the charge carriers to circularly polarized radiation [44, 45, 82–85] (or indeed magnetic fields [86, 87]) due to the helical spatial confinement.
Optical transitions
In order to understand how our double-gated nanohelix system interacts with electromagnetic radiation, we study the inter-subband momentum operator matrix element \(T^{g\rightarrow f}_{j} =\langle {f}|\boldsymbol {\hat {j}} \cdot \boldsymbol {\hat {P}}_{j} |{g}\), which is proportional to the corresponding transition dipole moment, and dictates the transition rate between subbands ψ f and ψ г . Here, \(\boldsymbol {\hat {j}}\) is the projection of the radiation polarization vector onto the coordinate axes (j =x,y , z ) and the respective self-adjoint momentum operators are [44, 45, 82–84]
$$ \boldsymbol{\hat{P}}_{x} =\boldsymbol{\hat{x}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\sin(\varphi)\frac{d}{d\varphi} + \frac{1}{2}\cos(\varphi) \right], $$ (15a) $$ \boldsymbol{\hat{P}}_{y}=-\boldsymbol{\hat{y}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\cos(\varphi)\frac{d}{d\varphi} - \frac{1}{2}\sin(\varphi) \right], $$ (15b) $$ \boldsymbol{\hat{P}}_{z}=-\boldsymbol{\hat{z}}\frac{i \hbar \rho}{\rho^{2} +R^{2}}\frac{d}{d\varphi}. $$ (15c)In terms of the dimensionless position variable φ , we are required to evaluate \(T^{g\rightarrow f}_{j} =\rho \int _{0}^{2\pi N}\psi _{f}^{\ast } P_{j} \psi _{g} d\varphi \), and upon substituting in from Eq. 4 we find
$$ {\begin{aligned} T^{g\rightarrow f}_{x} &=\frac{i \hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\ &\quad\left.-c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16a) $$ {\begin{aligned} T^{g\rightarrow f}_{y} &=\frac{\hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\&\left.\quad+c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16b) $$ T^{g\rightarrow f}_{z} =\frac{\hbar \rho}{\left(\rho^{2} + R^{2} \right)} \sum_{m} c_{m}^{\ast (f)} c_{m}^{(g)} (q+m). $$ (16c)We see from Eqs. 16a and 16b that light linearly polarized transverse to the helix axis couples coefficients with angular momentum differing by unity Δ м =± 1, whereas from Eq. 16c, linear polarization parallel to the helix axis couples only Δ м =0. In Fig. 5, we plot the absolute square of the momentum operator matrix element between the lowest three bands for linearly polarized light propagating perpendicular to the helix axis (i.e. with z -поляризация). Initially, for A г =C ⊥ =0, transitions between the ground and first bands are forbidden (as is to be expected for a unit cell with two equivalent wells resulting in a doubling of the first Brillouin zone, so it is in fact the same band). As the strength of the doubled period potential A г is increased with respect to B г , transitions become allowed away from q =0 as can be seen from Fig. 5a (following behaviour from the dotted red curve through to the solid blue curve). The parameters are swept through a resonance as we go from the solid to the dashed blue curve, wherein the situation changes drastically. To understand this behaviour, we must consider the special case of q =0. As we traverse this resonance, the energy of the Bloch function with q =0 constructed from the first excited state of the deeper well in the DQW unit cell (p -like) passes below the Bloch function constructed from the ground state in the shallower well (s -like). Consequently, the parity with respect to φ (which is a good quantum number only for q =0 or |q |=1/2) of the two excited states is exchanged resulting in the rapid switch from forbidden to allowed at q =0, wherein the z -polarized inter-subband matrix element becomes non-zero due to the operator \(\boldsymbol {\hat {P}}_{z}\) (see Eq. 15c) now coupling the even ground state with the odd first excited state. We therefore see the opposite behaviour for transitions between the ground and second band in Fig. 5b about q =0. While initially increasing A г allows transitions at q =0 between the ground state and the second excited state when it is p -like, beyond resonance (when the order of the s -like and p -like excited states are swapped) transitions are suppressed. See for example Ref. [88] for a clear picture of this interchange between the ordering of the even and the odd parity excited states. For transitions between the first and second band (Fig. 5c), we observe a large transition centred about q =0 due to the lifting of the m =± 1 degenerate states of the field-free helix by the superlattice potential. The presence of symmetry-breaking C ⊥ ruins the pristine parities of the states at the centre of the Brillouin zone and all transitions are allowed, as shown in the insets of Fig. 5.
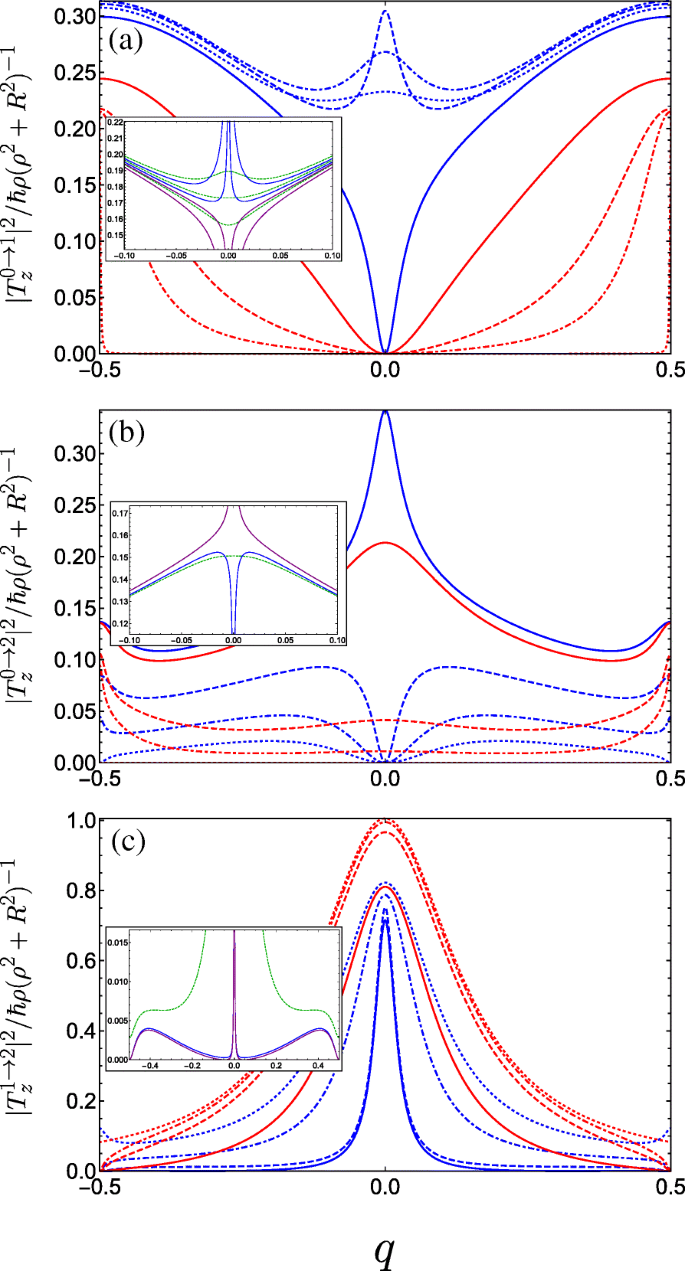
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by linearly z -polarized radiation and for a variety of parameter combinations spanning the first incident of resonance. The different blue curves keep A г =0.5 and C ⊥ =0 fixed and vary B г =0.1, 0.2, and 0.3 corresponding to dot-dashed, dashed, and solid. The different red curves keep B г =0.3 and C ⊥ =0 fixed while varying A г =0.05, 0.1 and 0.3 as dot-dashed, dashed, and solid, while the dotted blue (dotted red) plots the limiting case A г =0.5 &B г →0 (A г →0 &B г =0.3). а Transitions between the ground and first bands. The inset plots the behaviour for fixed A г =0.5 and changing B г crossing the resonant condition at B г =0.25 (see text) in a reduced q -range, ranging from upper blue B г =0.245, lower blue B г =0.249, upper purple B г =0.251, to lower purple B г =0.255. The dashed green curves are for small non-zero transverse field C ⊥ =0.05 ranging from B г =0.245 (upper curve) to B г =0.255 (lower curve) in increments of 0.05. б Plots transitions between the ground and second bands, the inset plots the behaviour close to resonance when A г =0.5; blue is B г =0.249, purple is B г =0.251, and dark green is at resonance with C ⊥ =0.05. c Plots transitions between the first and second bands, the parameters for the inset are the same as those in (b )
In Fig. 6, we plot the absolute square of the momentum operator matrix element for right-handed circularly polarized light which propagates along the helix axis, given by |T x +iT y | 2 . Notably, we observe a large anisotropy between the two halves of the first Brillouin zone, while the result for left-handed polarization is a mirror image to what we see in Fig. 6. Physically, this can be attributed to the conversion of the photon angular momenta to the translational motion of the free charge carriers projected onto the direction of the helix axis, with an unequal population of the excited subband in a preferential momentum direction controlled by the relative handedness of both the helix and the circular polarization of light. An intuitive mechanical analogue would be the rotary motion of Archimedes’ screw being converted into the linear motion of water along the direction of the screw axis dictated by the handedness of the thread. As such, our system of a double-gated nanohelix irradiated by circularly polarized light exhibits a photogalvanic effect, whereby one can choose the net direction of current by irradiating with either right- or left-handed circularly polarized light [44, 45, 89]. This differs from conventional one-dimensional superlattices, wherein the circular photogalvanic effect stems from the spin-orbit term appearing in the effective electron Hamiltonian and is consequently a weaker and hard-to-control phenomenon [90, 91]. The electric current induced by promoting electrons from the ground subband to an excited subband f via the absorption of circularly polarized light can be understood from the equation for the electric current contribution from the f th subband
$$ j_{f} =\frac{e}{2 \pi \rho} \int dq \left[ v_{f}(q) \tau_{f}(q) - v_{g}(q) \tau_{g} (q) \right] \Gamma_{CP}^{g \rightarrow f}(q), $$ (17)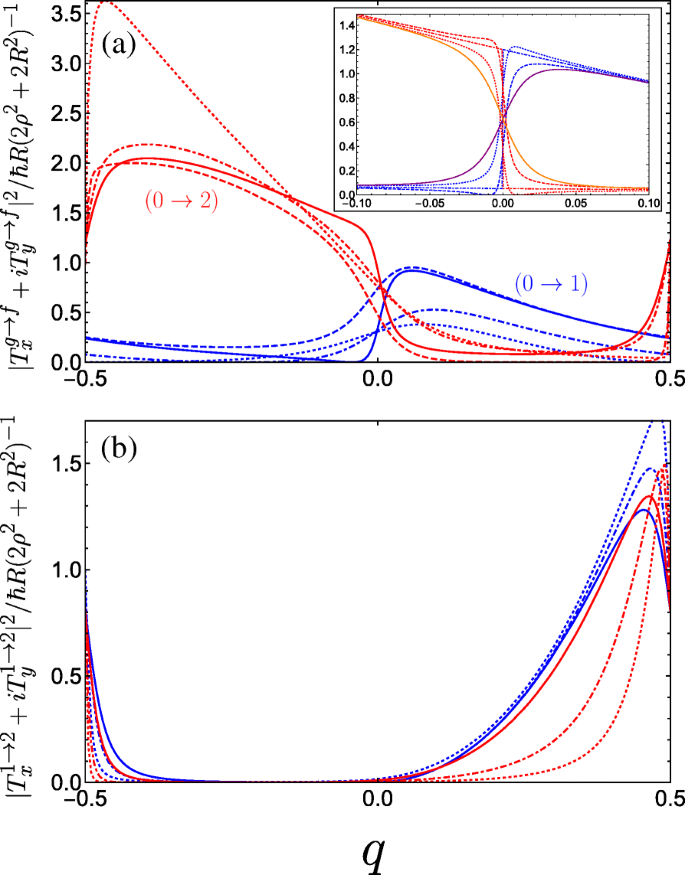
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by right-handed circularly polarized radiation |T x +iT y | 2 and for a variety of parameter combinations spanning the first incident of resonance. а The blue curves denote transitions between the ground and first band while the red curves denote transitions between the ground and second band, both with the following parameters:A г =0.5 and B г =0.3 for solid curves, A г =0.5 and B г =0.1 for dashed curves, A г =0.3 and B г =0.3 for dot-dashed curves, and A г =0.01 and B г =0.3 for dotted curves (as A г →0 the maximum of the 0→2 increases rapidly as it approaches q =− 1/2). The inset plots the behaviour as B г is tuned through resonance for A г =0.5; dotted is B г =0.24, dot-dashed is B г =0.25, and dashed is B г =0.26. The solid purple (orange) curve denotes transitions between the ground and first (second) band at resonance with C ⊥ =0.05 applied. б Plots transitions between the first and second bands. The different blue curves keep A г =0.5 fixed and vary B г =0, 0.2, and 0.3 corresponding to dotted, dot-dashed, and solid. The different red curves keep B г =0.3 fixed while varying A г =0.05, 0.1, and 0.3 as dotted, dot-dashed, and solid. We have omitted plots for C ⊥ ≠0 here as it yields no great qualitative change to the matrix elements
where \(v_{g,f}(q)=(\rho /\hbar)\partial \varepsilon _{g,f}/\partial q \) is the antisymmetric electron velocity v (q )=− v (− q ) (which we can deduce from the symmetric dispersion curves), τ g,f (q ) is a phenomenological relaxation time, and \(\Gamma _{CP}^{g \rightarrow f}(q)\) is the transition rate resulting from the optical perturbation of the electron system. Given that \(\Gamma _{CP}^{g \rightarrow f}(q) \propto |T_{x}^{g \rightarrow f} + i T_{y}^{g \rightarrow f}|^{2}\) for right-handed circularly polarized light where T x и T y are given by Eqs. 16a and 16b, respectively. The anisotropy present in Fig. 6a enters Eq. 17 to yield a non-zero photocurrent. This current flows in the opposite direction for left-handed polarization. Such a circular photogalvanic effect is also exhibited in chiral carbon nanotubes under circularly polarized irradiation [92, 93], although tunability predominantly stems from manipulating the nanotube physical parameters, which are hard to control. The double-gated nanohelix system offers superior versatility by fully controlling the landscape of the superlattice potential, which can be used to tailor the non-equilibrium asymmetric distribution function of photoexcited carriers (as shown in Fig. 6 for inter-subband transitions between the three lowest subbands).
On a side note, we expect that (as with chiral carbon nanotubes [93–95]) the application of a magnetic field along the nanohelix axis can take up the role played by circularly polarized radiation, whereby the current is induced by a magnetic-field-induced asymmetric energy dispersion—which in turn produces an anisotropic electron velocity distribution across the two halves of the Brillouin zone.
Выводы
In summary, we have shown that the system of a nanohelix between two aligned gates modelled as charged wires is a tunable binary superlattice. The band structure for this system exhibits a diverse behaviour, in particular revealing energy band crossings accessible via tuning the voltages on the gates. The application of an electric field normal to the plane defined by the gates and the helix axis introduces an additional parameter with which to open a band gap at these crossings. Engineering the band structure in situ with the externally induced superlattice potential along a nanohelix provides a clear advantage over conventional heterostructure superlattices with a DQW basis [96, 97]. Both systems can be used as high-responsivity photodetectors, wherein tailoring the band structure (to the so-called band-aligned basis [98–100]) can lead to a reduction in the accompanying dark current. Here control over the global depth of the quantum wells also permits versatility over the detection regime, which can lie within the THz range. We have also investigated the corresponding behaviour of electric dipole transitions between the lowest three subbands induced by both linearly and circularly polarized light, which additionally allows this system to be used for polarization sensitive detection. Finally, the ability to tune the system such that a degenerate excited state is optically accessible from the ground state, along with the inherent chirality present in the light-matter interactions, may make this a promising system for future quantum information processing applications [101]. It is hoped that with the advent of sophisticated nano-fabrication capabilities [102], fully controllable binary superlattice properties will be realized in a nanohelix and will undoubtedly contribute to novel optoelectronic applications.
Appendix
Touching energy bands at Brillouin zone boundary when A г =C ⊥ =0
Here, we show using matrix algebra that in the picture of a binary superlattice pairs of subbands touch at the Brillouin zone edges if A г =C ⊥ =0 and B г ≠0, as seen from the solid blue curves in Fig. 3a. Equation 5 is equivalent to the following N -by-N pentadiagonal matrix Hamiltonian with zeros on the leading sub- and superdiagonals:
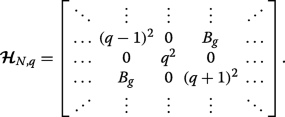 (18)
(18) Let us consider q =1/2 (we could alternatively take q =− 1/2) which makes the leading diagonal symmetric. We can then express this matrix Hamiltonian \(\widetilde {\mathcal {\boldsymbol {H}}}_{N} \equiv \boldsymbol {\mathcal {H}}_{N,q=1/2} \) in block form as
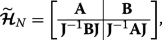 (19)
(19) где
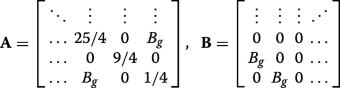 (20)
(20) are both of dimension N /2-by- N /2, and J is the exchange matrix. We may construct a matrix via permuting \(\boldsymbol {\mathcal {H}}_{N}\) with the N -by-N permutation matrix \(\boldsymbol {\mathcal {P}}_{N}\),
$$ \boldsymbol{\mathcal{P}}_{N} =\left[ \begin{array}{cccccc} 1 &0 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &\hdots &1 \\ 0 &1 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &1 &0 \\ \vdots &&&&&\vdots \\ 0 &\hdots &\hdots &1 &\hdots &0 \\ \end{array} \right], $$ (21)such that the permutation-similar matrix is
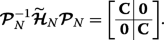 (22)
(22) Hence, the eigenvalues of \(\boldsymbol {\mathcal {P}}_{N}^{-1}\widetilde {\boldsymbol {\mathcal {H}}}_{N} \boldsymbol {\mathcal {P}}_{N}\), which are the same as the eigenvalues \(\widetilde {\boldsymbol {\mathcal {H}}}_{N}\), are double degenerate with the values given by the eigenvalue spectrum of the tridiagonal matrix C
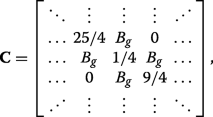 (23)
(23) which can also be expressed succinctly in terms of the previously defined matrices via \(\mathbf {C}=\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {A}\boldsymbol {\mathcal {P}}_{N/2}+\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {B}\mathbf {J}\boldsymbol {\mathcal {P}}_{N/2}^{4}\). We can see that applying C ⊥ ≠0 (inset of Fig. 3a) or both C ⊥ и A г ≠0 (inset of Fig. 3b) ruins the symmetry in the matrix Hamiltonian and prevents the existence of eigenvalues with multiplicity beyond unity, resulting in the appearance of band gaps.
Energy crossing at centre of Brillouin zone between third and forth subbands
As an example, let us specifically consider the case where p =2, wherein the matrices (12) and (13) become:
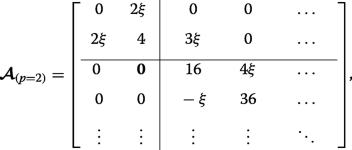 (24)
(24) and
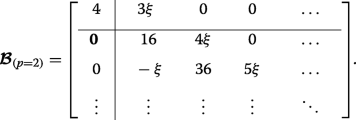 (25)
(25) This case corresponds to the crossings of the blue curves at the edge of the Brillouin zone in Fig. 3d (whereas p =0 results in crossings at q =0 in Fig. 3b). The lower eigenvalues are found exactly by diagonalizing each of the two finite matrices and they interlace, yielding \(\eta _{0,1,2} =2-\sqrt {4+4\xi ^{2}}, 4, 2+\sqrt {4+4\xi ^{2}}\). The infinite lower-right-hand block tridiagonal matrices coincide, thus the remaining double degenerate eigenvalues are found by approximately or numerically solving Det[D −η I ]=0.
Доступность данных и материалов
The data for the figures all stem from numerically diagonalizing the matrix described by Eq. 5 and can readily be achieved in any numerical software package. With this in mind, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Наноматериалы



