Переполнение двоичного кода

Одно предостережение в отношении двоичных чисел со знаком - это переполнение, когда ответ на проблему сложения или вычитания превышает величину, которую можно представить с помощью выделенного количества бит. Помните, что место знакового бита фиксировано с самого начала проблемы.

В последнем примере задачи мы использовали пять двоичных битов для представления величины числа и крайний левый (шестой) бит как бит отрицательного веса или знака. С пятью битами для представления величины у нас есть диапазон представления 2 ⁵ , или тридцать два целых шага от 0 до максимума.

Это означает, что мы можем представить число до +31 ₁₀ (011111 ₂ ) или всего -32 ₁₀ (100000 ₂ ).

Ограничения шестибитного числового поля

Если мы создадим задачу сложения с двумя двоичными числами, шестой бит будет использоваться для знака, и результат либо превысит +31 ₁₀ или меньше -32 ₁₀ , наш ответ будет неверным. Давайте попробуем добавить 17 ₁₀ и 19 ₁₀ чтобы увидеть, как это условие переполнения работает для чрезмерно положительных чисел:

Ответ (100100 ₂ ), интерпретируемый шестым битом как -32 ₁₀ место, фактически равно -28 ₁₀ , а не +36 ₁₀ как мы должны получить с +17 ₁₀ и +19 ₁₀ сложены вместе! Очевидно, это неверно. Что пошло не так?

Ответ кроется в ограничениях поля шестибитного числа, с которым мы работаем. Поскольку величина истинной и правильной суммы (36 ₁₀ ) превышает допустимый предел для нашего назначенного битового поля, возникает ошибка переполнения .

Проще говоря, шесть знаков не дают достаточно битов для представления правильной суммы, поэтому любое число, которое мы получим, используя стратегию отбрасывания самого левого бита переноса, будет неверным.

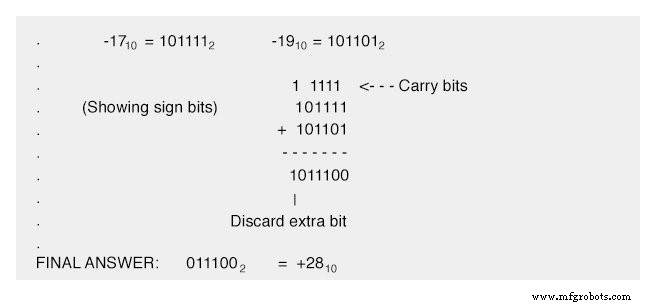
Аналогичная ошибка произойдет, если мы сложим два отрицательных числа вместе, чтобы получить сумму, которая слишком мала для нашего шестибитного двоичного поля. Давайте попробуем добавить -17 ₁₀ и -19 ₁₀ вместе, чтобы посмотреть, как это работает (или не работает, в зависимости от обстоятельств!):

(Неправильный) ответ - положительный двадцать восемь. Тот факт, что реальная сумма отрицательных семнадцати и отрицательных девятнадцати была слишком мала для правильного представления с помощью пятибитового поля величины и шестого знакового бита, является основной причиной этой трудности.

Использование седьмого бита для знакового бита

Давайте попробуем эти две задачи еще раз, за ​​исключением того, что на этот раз мы будем использовать седьмой бит для знакового бита и разрешить использование 6 битов для представления величины:

Используя достаточно большие битовые поля, чтобы обрабатывать величину сумм, мы приходим к правильным ответам. В этих примерах задач мы смогли обнаружить ошибки переполнения, выполнив задачи сложения в десятичной форме и сравнив результаты с двоичными ответами.

Например, при добавлении +17 ₁₀ и +19 ₁₀ вместе мы знали, что ответ был предполагаемым быть +36 ₁₀ , поэтому, когда двоичная сумма оказалась равной -28 ₁₀ , мы знали, что что-то должно быть не так. Хотя это допустимый способ обнаружения переполнения, он не очень эффективен.

В конце концов, вся идея дополнения состоит в том, чтобы иметь возможность надежно складывать двоичные числа вместе и не нужно перепроверять результат, складывая одни и те же числа в десятичной форме! Это особенно верно для целей построения электронных схем для сложения двоичных величин:схема должна иметь возможность проверять себя на переполнение без наблюдения человека, который уже знает правильный ответ.

Нам нужен простой метод обнаружения ошибок, не требующий дополнительных арифметических действий. Возможно, наиболее элегантным решением будет проверка наличия знака суммы и сравните ее со знаками добавленных чисел.

Очевидно, что два положительных числа, сложенные вместе, должны дать положительный результат, а два отрицательных числа, сложенные вместе, должны дать отрицательный результат. Обратите внимание, что всякий раз, когда у нас было условие переполнения в примерах задач, знак суммы всегда был противоположным из двух сложенных чисел:+17 ₁₀ плюс +19 ₁₀ давая -28 ₁₀ , или -17 ₁₀ плюс -19 ₁₀ что дает +28 ₁₀ .

Проверяя только знаки, мы можем сказать, что что-то не так. Но как насчет случаев, когда положительное число добавляется к отрицательному? Под каким знаком должна быть сумма, чтобы она была верной. Или, точнее, какой знак суммы обязательно укажет на ошибку переполнения?

Ответ на этот вопрос столь же элегантен: никогда не будет ошибка переполнения при сложении двух чисел с противоположными знаками! Причина этого становится очевидной, если учесть характер переполнения. Переполнение происходит, когда величина числа превышает диапазон, разрешенный размером битового поля.

Сумма двух чисел с одинаковым знаком может очень хорошо превышать диапазон битового поля этих двух чисел, поэтому в этом случае возможно переполнение. Однако, если положительное число добавляется к отрицательному, сумма всегда будет ближе к нулю, чем любое из двух добавленных чисел:ее величина должна быть меньше, чем величина любого исходного числа, и поэтому переполнение невозможно.

К счастью, этот метод обнаружения переполнения легко реализуется в электронных схемах, и это стандартная функция в схемах цифрового сумматора:тема для более поздней главы.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист двоичной математики