Теплопроводность двух типов двумерных аллотропов углерода:исследование молекулярной динамики

Введение

Углеродные материалы, например алмаз [1], углеродные нанотрубки [2,3,4,5] и графен [6,7,8,9,10,11,12], вызвали огромный исследовательский интерес из-за их превосходных свойств. теплопередающие свойства. Особенно низкоразмерные углеродные материалы демонстрируют выдающиеся свойства теплопередачи. В качестве одномерного материала высокая теплопроводность (TC) одиночной углеродной нанотрубки наблюдалась экспериментально [2, 3] и теоретическими исследованиями [4, 5]. Более того, как плоский двумерный (2D) углеродный материал толщиной в один атом, графен считается революционным материалом для будущего поколения теплопроводных армированных композитов из-за его высокой TC [6,7,8,9,10 , 11,12]. Также сообщается, что ОС графина может достигать 40% от графена, и это имеет потенциальное применение в управлении температурой [13,14,15].

Вдохновленные захватывающими характеристиками этих углеродных аллотропов, исследователи в последние годы прилагают интенсивные усилия по изучению углеродных аллотропов и их производных. Экспериментальный и теоретический подходы были приняты для исследования новых двумерных аллотропов углерода, таких как sp ² -подобный углеродный слой с пяти-, шести- и семичленными кольцами [16]; 2D аморфный углерод с четырехчленными кольцами [17]; планарный углеродный пентагептит [18]; 2D углеродный полупроводник с узорчатыми дефектами [19]; несколько 2D плоских углеродных сетей [20]; октаграфен [21]; Т-графен [22]; и H-сеть [23]. Идентификация уникальных свойств этих двумерных углеродных аллотропов имеет важное значение для будущих поколений наноматериалов в электронных, фотонных и тепловых полях [16,17,18,19,20,21,22,23].

С растущим интересом к исследованию новых структур двумерных аллотропов углерода Su et al. [24] предложили два новых энергетически конкурентоспособных и кинетически стабильных двумерных аллотропа углерода, состоящих из восьмиугольников и пятиугольников, с помощью расчетов из первого принципа. Кинетическая стабильность этих двух углеродных листов была подтверждена расчетом их фононных дисперсионных кривых. В связи с тем, что структуры этих двух углеродных аллотропов можно рассматривать как копирование ленты из пяти-пяти-восьмичленных колец (558) вдоль прямой линии и вдоль зигзагообразного пути, эти два углеродных аллотропа, таким образом, называются восьмиугольниками и пятиугольник-графен-линия (OPG-L) и восьмиугольник и пятиугольник-графен-зигзаг (OPG-Z) соответственно. Энергия образования этих двух аллотропов углерода составляет 0,31 эВ / атом и 0,34 эВ / атом соответственно. Эти значения намного ниже энергии образования ранее синтезированного графина, т.е. 0,76 эВ / атом [25]. Отмечено, что OPG-Z обладает замечательной анизотропией электронной структуры, которая имеет потенциальное применение в электронных устройствах [24]. Следовательно, чтобы соответствовать требованиям электронных приложений OPG-L и OPG-Z, неизбежно и необходимо исследовать свойства рассеивания тепла двух новых структур. До сих пор термические свойства этих двух структур все еще не ясны.

В этой работе мы исследуем термические свойства двух новых двумерных аллотропов углерода с помощью моделирования молекулярной динамики. Исследовано влияние размера, деформации и температуры на TC. Результаты анализируются путем расчета плотности колебательных состояний (ВДОС) фононов. Наше исследование тепловых свойств этих двух углеродных аллотропов указывает на их потенциальное применение в устройствах управления температурой.

Модель и методы

Структуры OPG-L (рис. 1a) и OPG-Z (рис. 1b) содержат репрезентативные ячейки, состоящие из восьмиугольников и пятиугольников [24]. Чтобы различать типы краев структур, мы определяем хиральность кресло и зигзаг, как и графен (см. Рис. 1). Эти две структуры могут быть образованы репрезентативной лентой 558, обозначенной красными атомами, с использованием трансляционной симметрии вдоль зеленых рядов.

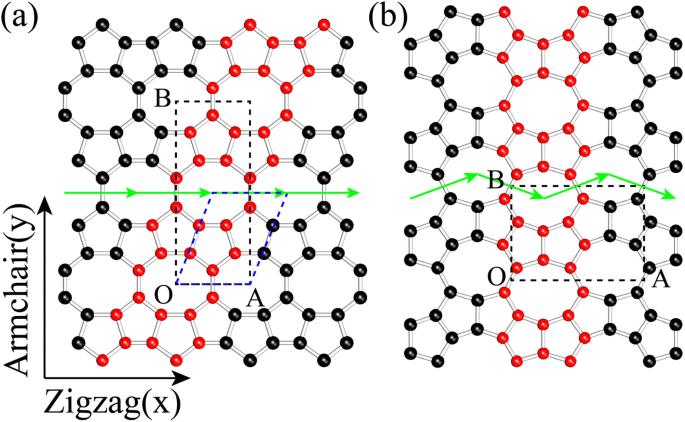
Схематические модели а OPG-L и b ОПГ-З. Черные пунктирные рамки - ортогональные элементарные ячейки OPG-L и OPG-Z, где OA и OB - векторы решетки. Примитивная ячейка OPG-L показана в синей пунктирной рамке, в то время как примитивная ячейка OPG-Z такая же, как и кристаллическая ячейка

Все моделирование методом МД выполняется с использованием пакета крупномасштабного атомно-молекулярного массово-параллельного симулятора (LAMMPS) [26]. Мы используем оптимизированный потенциал Терсоффа Линдсея и Бройдо [27] с небольшими изменениями, то есть модифицированный оптимизированный потенциал Терсоффа, для описания взаимодействий между атомами углерода. Линдси и Бродио оптимизировали два параметра по сравнению с исходным потенциалом Терсоффа [28], один для равновесного угла связи и один для силы притягивающего взаимодействия. Согласно этому оптимизированному потенциалу Терсоффа [27], равновесная длина связи в графене составляет 1,4388 Å, что больше экспериментального значения 1,42 Å [29]. Поскольку единственными параметрами, связанными с длиной в потенциале Терсоффа, являются λ ₁ в отталкивающей функции ( f ^R = А ехр. (- λ ₁ г )) и λ ₂ в привлекательной функции ( f ^А = B ехр (- λ ₂ г )), мы можем получить правильную длину связи, умножив эти два параметра на коэффициент 1,4388 / 1,42. То есть меняем λ ₁ от 3,4879 Å ⁻¹ до 3,5333 Å ^-1 и изменим λ ₂ от 2,2119 Å ⁻¹ до 2,2407 Å ^{- 1} . Эти модификации только глобально изменяют масштаб длины потенциала. На основе этого модифицированного оптимизированного потенциала Терсоффа соответствующие параметры равновесной решетки в МД-моделировании следующие:OA =3,63 Å, OB =9,38 Å в OPG-L и OA =6,78 Å, OB =5,04 Å в OPG-Z, которые являются в хорошем согласии с предыдущим исследованием Su et al. [24], то есть OA =3,68 Å, OB =9,12 Å в OPG-L и OA =6,90 Å, OB =4,87 Å в OPG-Z.

Моделирование обратной неравновесной молекулярной динамики (rNEMD) [30] выполняется для расчета TC. Периодические граничные условия приняты в размерах x и y. Структуры OPG-L и OPG-Z изначально оптимизированы с помощью версии алгоритма сопряженного градиента Polak-Ribiered [31], а затем используется термальная ванна Нозе-Гувера с длительностью 0,25 нс [32, 33], чтобы гарантировать, что система достигает состояние равновесия при 300 К (с шагом по времени 0,25 фс). После достижения равновесного состояния модель разбивается на 50 плит по направлению теплопередачи. Как показано на рис. 2а, 1-я пластина предназначена для теплоотвода, а 26-я (средняя пластина образца) является источником тепла, и тепловой поток передается от источника тепла (горячая область) к радиатору ( холодный регион). Направление переноса теплового потока определяется как направление длины (L), а поперечное направление - это направление ширины (W). Тепловой поток J высвобождается / впрыскивается между этими двумя пластинами за счет обмена кинетической энергией между самым горячим атомом, имеющим самую высокую кинетическую энергию, в пластине радиатора и самым холодным атомом, имеющим самую низкую кинетическую энергию, в источнике тепла. плита. Тепловой поток J может быть получен путем расчета количества обмена кинетической энергией между теплоотводом и плитой источника тепла в соответствии со следующими уравнениями.

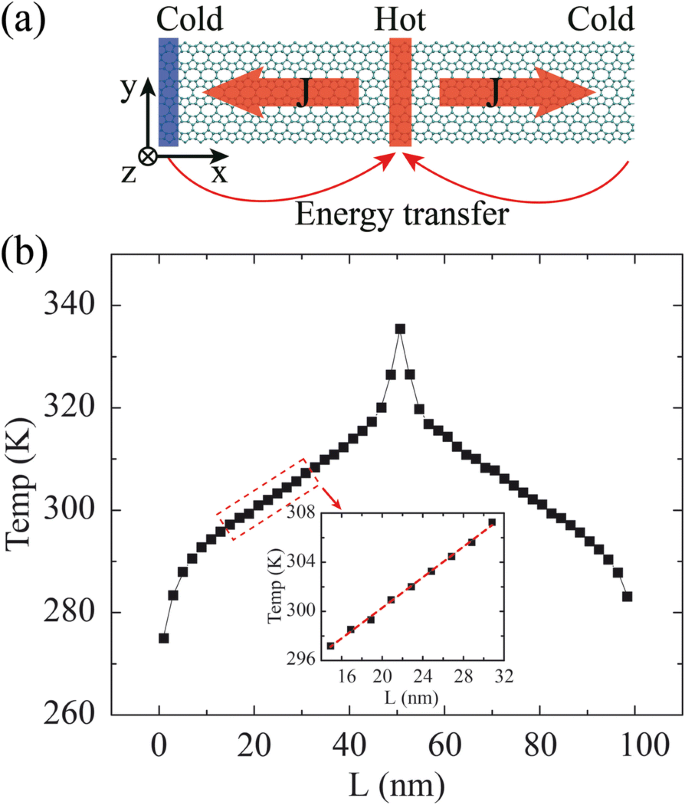
а Схематическое изображение метода rNEMD. Тепловой поток передается от источника тепла (горячая область) к радиатору (холодная область). Направление переноса теплового потока определяется как направление длины (L), а поперечное направление - это направление ширины (W). б Распределение средней температуры в зависимости от плит

где t _своп - полное время обмена кинетической энергией, N _своп обозначает количество обменивающихся пар атомов, m - масса атома, а v _h и v _c представляют скорость обмена атомами (самый горячий атом с самой высокой кинетической энергией в пластине теплоотвода и самый холодный атом с самой низкой кинетической энергией в пластине источника тепла) соответственно. Температура каждой плиты собирается и усредняется за 3,0 нс для получения распределения температуры, когда система достигает неравновесного устойчивого состояния (через 1,5 нс). Значение TC ( κ ) затем вычисляется с использованием закона Фурье как

где A - площадь поперечного сечения теплопередачи ( A получается путем умножения ширины и толщины модели) и ∂T / ∂L обозначает градиент температуры после того, как система достигает неравновесного стационарного состояния (см. рис. 2b). Коэффициент 2 отражает тот факт, что тепловой поток переносится в двух направлениях от источника тепла. Толщина модели принимается равной межслоевому равновесному расстоянию графена (0,34 нм) [8, 10, 34, 35].

Результаты и обсуждения

Сначала мы исследуем влияние размера системы на ОС двух углеродных аллотропов. Образцы моделирования генерируются с одинаковой шириной 3 нм, но разной длиной от 50 до 1000 нм. Следует отметить, что все значения длины выборки, упомянутые в этой работе, являются эффективной длиной ( L _эфф ) теплопередачи. То есть эффективная длина выборки составляет половину длины выборки ( L ), т.е. L _эфф = L / 2, что объясняется передачей теплового потока от середины (источника тепла) к обоим концам (теплоотвод) образца в методе rNEMD. В частности, мы подтвердили, что TC не зависит от ширины образца, путем расчета теплопроводности образцов с фиксированной длиной 50 нм, но с различной шириной 3 нм, 6 нм, 9 нм и 12 нм соответственно, как показано на Рис. 3. ТК OPG-L по зигзагообразному и кресельному направлениям обозначены как κ . _OPG-LZ и κ _OPG-LA , соответственно. Аналогично κ _OPG-ZZ и κ _OPG-ZA используются для представления ТК OPG-Z по зигзагообразному и кресельному направлениям. Результаты моделирования показывают, что TC OPG-L и OPG-Z в двух хиральных направлениях монотонно возрастает при изменении длины образца от 50 до 1000 нм. Это связано с тем, что в длинном образце в теплообмене участвуют акустические фононы с большей длиной волны [9, 36]. Соответственно, ОС OPG-L и OPG-Z длиной 50 и 1000 нм вдоль зигзагообразного направления равны κ _OPG-LZ50 =125 Вт / мК, κ _OPG-LZ1000 =296 Вт / мК, κ _OPG-ZZ50 =94 Вт / мК и κ _OPG-ZZ1000 =236 Вт / мК. В направлении кресла ТК OPG-L и OPG-Z имеют κ _OPG-LA50 =105 Вт / мК, κ _OPG-LA1000 =316 Вт / мК, κ _OPG-ZA50 =93 Вт / мК и κ _OPG-ZA1000 =214 Вт / мК.

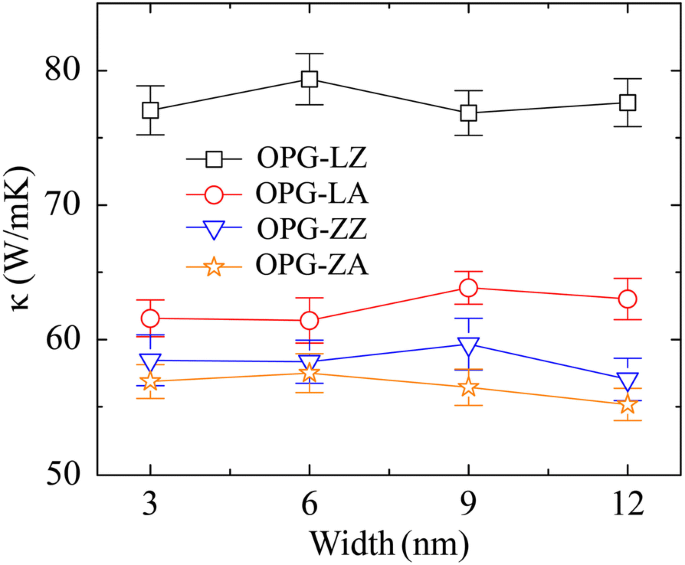
TC OPG-L и OPG-Z в зависимости от ширины

Чтобы извлечь TC из бесконечно длинных образцов, используется процедура обратной подгонки. Связь между обратной длиной и обратным TC выражается как [37,38,39]:

где κ _∞ - экстраполированный TC бесконечной выборки, l - длина свободного пробега фонона, а L _эфф - эффективная длина теплопередачи. Уравнение (3) предполагает, что зависимость между обратной длиной и обратной TC должна быть линейной. Как показано на рис. 4, наблюдается линейная зависимость между обратной длиной и обратной TC. Путем экстраполяции на L ⁻¹ =0, TC бесконечных выборок, т. Е. κ _OPG-LZ =310 Вт / мК, κ _OPG-LA =332 Вт / мК, κ _OPG-ZZ =247 Вт / мК, а κ _OPG-ZA =228 Вт / мК.

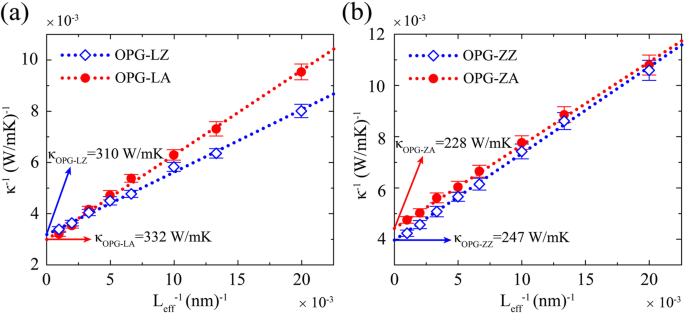
Обратный TC для a OPG-L и b OPG-Z как функция обратной длины образца при 300 К. Незакрашенный синий ромб и красные пятна представляют собой TC вдоль зигзага и направления кресла, соответственно

Кроме того, мы также выражаем текущую TC в методе равновесной молекулярной динамики (EMD), устанавливая образец с одинаковой длиной и шириной 20 нм (этот размер образца моделирования был протестирован, чтобы быть достаточно большим, чтобы исключить эффекты конечного размера) . Согласно работе Fan et al. [39, 40] расчет TC в методе EMD основан на формуле Грина-Кубо [41, 42], в которой бегущий TC вдоль направления x может быть выражен следующим образом:

где κ _B постоянная Больцмана, V объем системы, T - абсолютная температура системы, 〈 Дж _x (0) Дж _x ( т ^' )〉 - автокорреляционная функция теплового потока, t - время корреляции, а J _x - тепловой поток в направлении x. Символ 〈〉 представляет среднее время в симуляциях EMD. Максимальное время корреляции составляет 2 нс, что, как было проверено, достаточно велико. Как показано на рис. 5, текущие TC для OPG-L и OPG-Z в двух хиральных направлениях при 300 K выражаются усреднением результатов 100 независимых симуляций с различной начальной скоростью. Мы можем дополнительно получить TC бесконечной выборки, усредняя текущее TC за время корреляции от 1,0 до 2,0 нс. То есть конвергентные ТС OPG-LZ, OPG-LA, OPG-ZZ и OPG-ZA составляют 313 Вт / мК, 344 Вт / мК, 261 Вт / мК и 233 Вт / мК соответственно, которые находятся в разумное согласие с результатами экстраполяции в методе rNEMD.

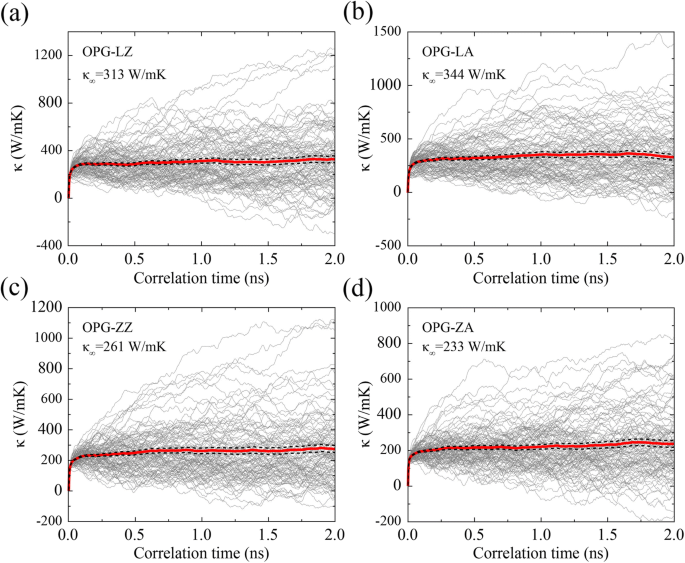
Эволюция ТК а OPG-LZ, b OPG-LA, c OPG-ZZ и d OPG-ZA при 300 K как функция времени корреляции. Тонкие линии представляют результаты 100 независимых расчетов, а толстые сплошные и пунктирные линии представляют их средние значения и границы ошибок. κ _∞ является TC бесконечной выборки, которая получается усреднением текущего TC за время корреляции от 1,0 до 2,0 нс

Установлено, что ОС этих двух углеродных аллотропов намного ниже, чем у графена (3000–5000 Вт / мК) [7, 43] . Чтобы объяснить это явление и изучить физическую картину, мы вычисляем три важных параметра, т. Е. C _v , v _г , и l , основанный на классическом решеточном уравнении теплопереноса:

где C _v - теплоемкость, v _г эффективная групповая скорость фононов, l - длина свободного пробега фононов.

Образец с длиной и шириной 20 нм принят для исследования теплоемкости при 300 К. Теплоемкость вычисляется в соответствии с подходом МакГоги и Кавиани [44], который использовался в приближении к равновесной молекулярной динамике. моделирования [45]. Рассчитываем полную энергию E при температуре T =290 K, 295 K, 300 K, 305 K, 310 K в каноническом ансамбле, и результаты усредняются за 60 пс десяти независимых симуляций с различной начальной скоростью. Как показано на рис. 6, наклон линейной аппроксимации кривой энергия-температура представляет собой теплоемкость.

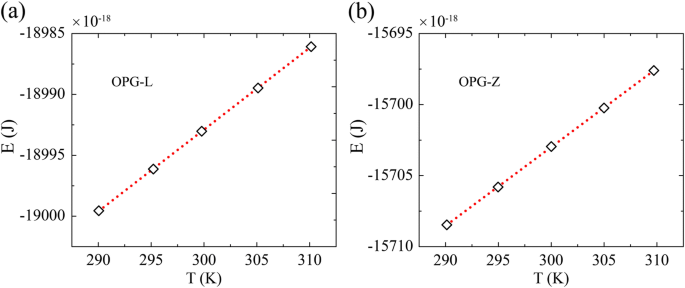
Изменение энергии как функция температуры для a OPG-L и b ОПГ-З. Наклон кривой энергия-температура обозначает теплоемкость. Соответствующие теплоемкости составляют 4,163 Е-23 Дж / К и 4,126 Е-23 Дж / К соответственно на атом

Следует отметить, что вычисляемая нами групповая скорость фононов является эффективной групповой скоростью фононов v _г а не средняя групповая скорость фононов v . Как показано на рис. 7, эффективная групповая скорость фононов может быть получена путем сравнения результатов моделирования rNEMD и EMD. То есть эффективная длина системы L _эфф можно определить в методе EMD, умножив верхний предел времени корреляции t в формуле Грина-Кубо Eq. (4) эффективной групповой скоростью фононов v _г , L _эфф ≈ v _г т . Бегущий ТК κ ( т ) метода EMD также можно рассматривать как функцию длины системы κ ( L _эфф ). По сравнению со средней групповой скоростью фононов, эффективная групповая скорость фононов является приблизительной оценкой, но она широко использовалась при изучении теплопереноса в низкоразмерных решеточных моделях [46], а также для графена [40] и аллотропов Si [39].

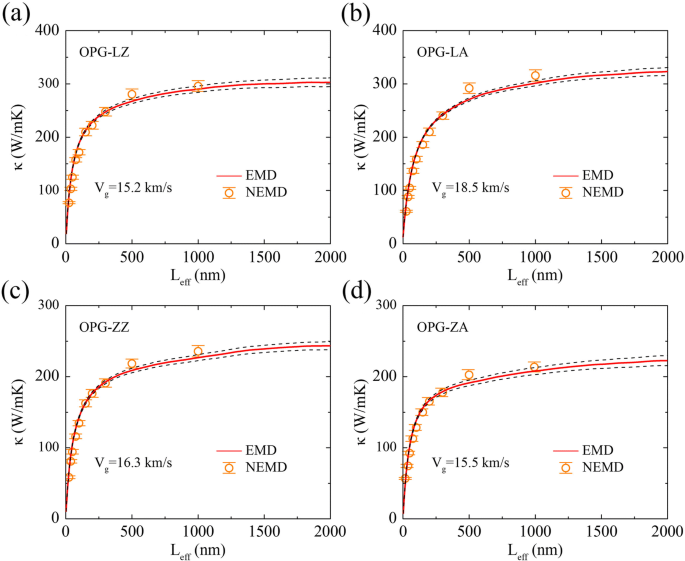
TC of a OPG-LZ, b OPG-LA, c OPG-ZZ и ( d ) OPG-ZA как функция эффективной длины выборки из моделирования EMD и rNEMD. Эффективная групповая скорость фононов V _г получается путем объединения моделирования EMD и rNEMD

На основании уравнения. Согласно (3) длина свободного пробега фонона может быть получена экстраполяцией в методе rNEMD. Чтобы сравнить TC этих двух углеродных аллотропов с TC графена, мы также представляем эти три параметра графена. Теплоемкость графена рассчитывается указанным выше методом, а эффективная групповая скорость фононов и длина свободного пробега фононов получены в других работах [7, 40]. Можно обнаружить, что теплоемкости этих двух аллотропов углерода близки к теплоемкости графена; однако эффективная групповая скорость и длина свободного пробега фононов намного ниже, чем у графена, что приводит к более низкой TC для двух материалов (см. Таблицу 1).

Кроме того, мы исследуем зависимость TC от температуры, как показано на рис. 8. Температурный диапазон от 200 K до 300 K является основным диапазоном, на котором мы сосредоточены. Образцы для моделирования генерируются с одинаковой шириной 3 нм, но разной длиной 50 нм, 75 нм, 100 нм, 150 нм и 200 нм соответственно. Как показано на рис. 8a, b, мы даем обратную TC для OPG-LZ и OPG-LA при различных температурах как функцию обратной длины образца. Подобно экстраполяции размерного эффекта при 300 К, теплопроводность бесконечного образца при различных температурах извлекается путем экстраполяции. Как показано на рис. 8c, d, все сведенные значения теплопроводности нормированы TC при 300 K ( κ ₀ ).

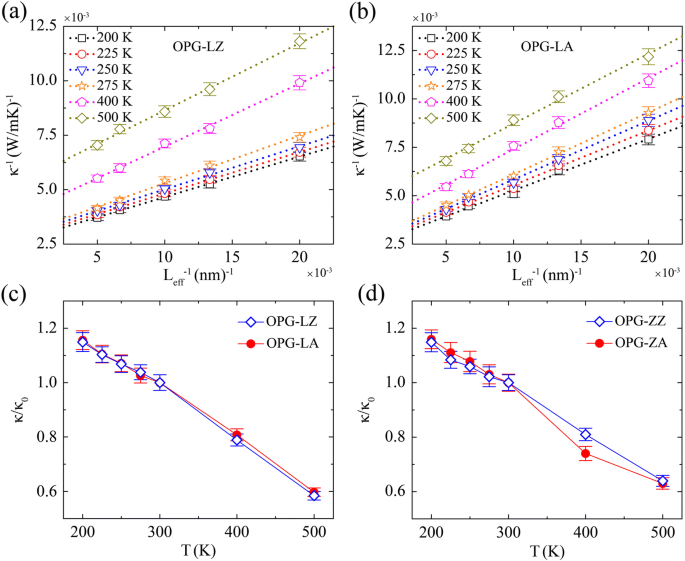
Обратный TC для a OPG-LZ, b OPG-LA при различных температурах в зависимости от обратной длины образца и относительной TC ( κ / κ ₀ ) из c OPG-L и d OPG-Z как функция температуры. κ ₀ - ТС при 300 К, что составляет 310 Вт / мК, 332 Вт / мК, 247 Вт / мК и 227 Вт / мК для κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ , и κ _OPG-ZA соответственно

Рисунок 8 показывает, что как в направлении зигзага, так и в направлении кресла, TC уменьшается с увеличением температуры как для OPG-L, так и для OPG-Z. Тенденция изменения TC в зависимости от температуры (от 200 до 500 K) хорошо согласуется с предыдущими исследованиями TC графена [8, 36, 47]. Это явление происходит из-за усиления процессов рассеяния переброса, которые играют критическую роль в переносе тепла [8, 36, 47]. Кроме того, при изменении температуры от 300 до 500 К значение κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ , и κ _OPG-ZA снижается на 42%, 40%, 36% и 37% соответственно. Зависимость TC этих двух углеродных аллотропов от температуры показывает, что необходимо учитывать температурные эффекты для их практического применения.

Тепловые свойства двумерных материалов, например графена [48, 49], силицена [34, 50, 51] и фосфора [37], чувствительны к инженерии деформации. Сообщалось, что TC графена с малым размером уменьшается с увеличением деформации растяжения [48], и TC также может быть увеличена за счет увеличения деформации, когда размер образца превышает 500 мкм [49]. Необычные зависимости TC от размера и деформации образца объясняются конкуренцией между граничным рассеянием и фонон-фононным рассеянием. Кроме того, TC силицена увеличивается при небольшой деформации растяжения, но уменьшается при большой деформации из-за конкуренции между смягчением фононов в плоских модах и усилением фононов в модах вне плоскости [34, 50, 51]. Следовательно, важно и необходимо изучить взаимосвязь между поведением ТС и деформацией при растяжении как для конструкций OPG-L, так и для OPG-Z.

Сначала мы исследуем механические свойства этих двух аллотропов углерода. Размер образца составляет около 5 нм в длину и 5 нм в ширину. Чтобы избежать любых ложных высоких сил связи и нефизического упрочнения [52, 53], расстояние отсечки фиксировано на ( R = S =1,95 Å). Это расстояние отсечки в модифицированном оптимизированном потенциале Терсоффа также согласуется с таковым в предыдущих потенциалах Терсоффа (1,8–2,1 Å) [28, 53,54,55], которые используются для моделирования связи C-C. Все моделирование начинается с расслабления атомистической конфигурации структуры до состояния с минимальной потенциальной энергией. Применяется одноосная деформация растяжения со скоростью 0,0002 пс ⁻¹ . Следует отметить, что равновесное расстояние между слоями графена (3,4 Å) используется для представления равновесного расстояния между слоями двух структур. Механические свойства этих двух углеродных аллотропов перечислены в таблице 2 со сравнением графина и графена [56]. Надстрочные характеристики z и a представляют собой зигзагообразные листы и листы кресел соответственно.

Из таблицы 2 видно, что в зигзагообразном направлении модуль Юнга OPG-L и OPG-Z составляет 538 ГПа и 492 ГПа, а в направлении кресла модуль Юнга составляет 648 ГПа и 550 ГПа, соответственно. Это указывает на то, что модуль Юнга OPG-L и OPG-Z близок к модулю графина (503,1 ^z и 525,0 ^a ), но ниже, чем у графена (856,4 ^z и 964.0 ^a ). Отношения между напряжением и деформацией двух углеродных аллотропов вдоль зигзагообразного и кресельного направлений показаны на рис. 9. В соответствии с характером разрушения этих двух углеродных аллотропов мы дополнительно получаем предельную деформацию (растяжение) этих двух углеродных аллотропов. Соответственно, в направлении зигзага предельная деформация (растяжение) OPG-L и OPG-Z составляет 17,2% и 10,9%, а в направлении кресла предельная деформация (растяжение) составляет 8,7% и 7,9%. Мы обнаружили, что конструкция ОПГ-Л имеет более высокую прочность при растяжении в зигзагообразном направлении. Однако по сравнению с графином и графеном предельная деформация (напряжение) двух аллотропов углерода ниже.

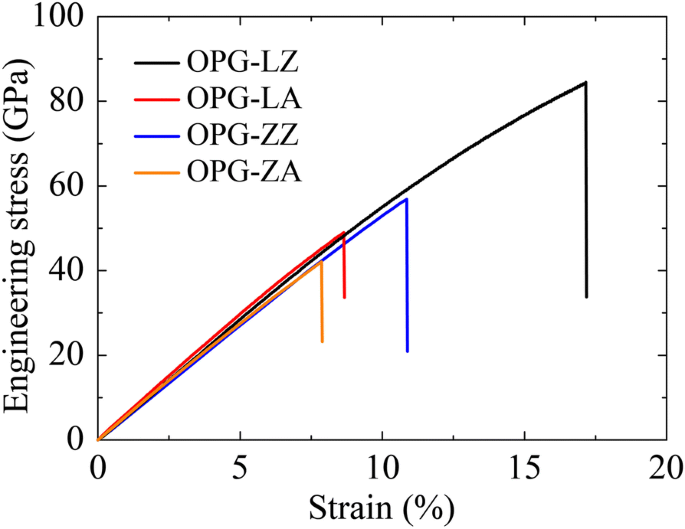
Отношения напряжения и деформации двух углеродных аллотропов в зигзагообразном и кресельном направлениях

Затем мы изучаем влияние деформации на TC этих двух углеродных аллотропов, применяя одноосную деформацию растяжения вдоль направления теплопередачи. Образцы для моделирования имеют одинаковую ширину 3 нм, но разную длину 50 нм, 75 нм, 100 нм, 150 нм и 200 нм соответственно. Значения теплопроводности бесконечного образца при различных деформациях извлекаются путем экстраполяции (см. Рис. 10a, b). Как показано на рис. 10c, d, все сведенные значения теплопроводности нормированы на TC без напряжения при 300 K ( κ ₀ ), далее зададим относительную TC ( κ / κ ₀ ) двух аллотропов углерода в зависимости от различных одноосных деформаций. Рисунок 10 ясно показывает, что TC как OPG-L, так и OPG-Z монотонно уменьшается с увеличением деформации растяжения, что согласуется с предыдущими исследованиями графена [34, 48], но резко контрастирует с силиценом [34, 50, 51] и фосфорен [37]. Как показано на рис. 10, максимальное уменьшение κ _OPG-LZ , κ _OPG-LA , и κ _OPG-ZZ , κ _OPG-ZA составляют 49%, 44%, 37% и 31% соответственно. В частности, TC OPG-L вдоль зигзагообразного направления можно регулировать посредством деформации в большом диапазоне.

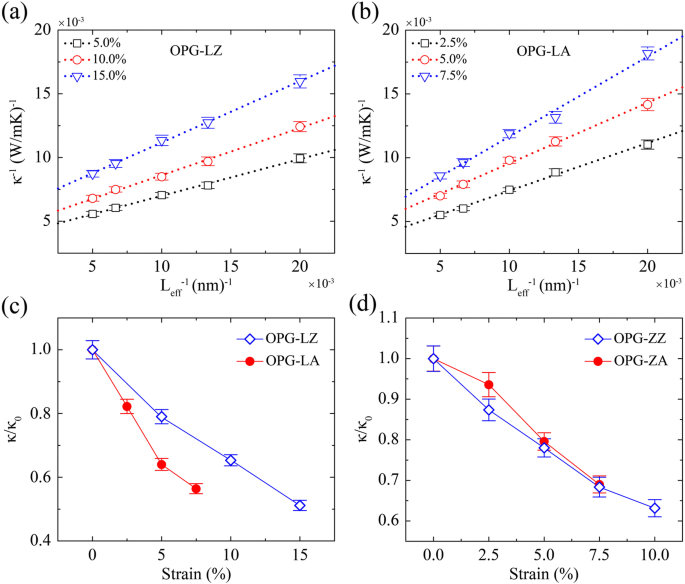
Обратный TC для a OPG-LZ, b OPG-LA при различных одноосных деформациях в зависимости от обратной длины образца и относительной TC ( κ / κ ₀ ) из c OPG-L и d OPG-Z как функция деформации. κ ₀ это TC без напряжения при 300 K, который составляет 310 Вт / мК, 332 Вт / мК, 247 Вт / мК и 227 Вт / мК для κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ , и κ _OPG-ZA соответственно

Чтобы дополнительно выяснить влияние деформации на теплопередающие свойства OPG-L и OPG-Z, мы рассчитали VDOS фононов OPG-LZ при типичной деформации. VDOS вычисляются с помощью преобразования Фурье автокорреляционной функции атомной скорости. Функция определяется следующим образом:

Как показано на рис. 11, наблюдается смягчение фононов (красное смещение) как в плоскости, так и вне плоскости. Это явление хорошо согласуется с предыдущими исследованиями графена при деформации растяжения [34, 48]. В частности, по сравнению с VDOS в направлении вне плоскости, смягчение фононов в направлении в плоскости очевидно. Это указывает на то, что снижение ОС OPG-L и OPG-Z в основном происходит из-за вызванного деформацией смягчения фононов в направлении плоскости.

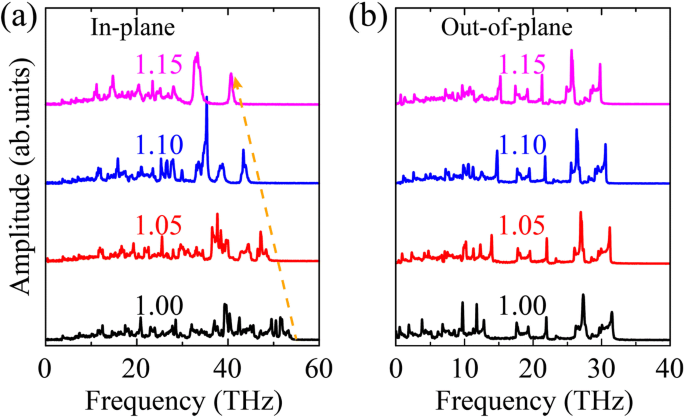
В самолете а и вне плоскости b VDOS OPG-L в зависимости от деформации одноосного растяжения вдоль зигзагообразного направления

Выводы

Таким образом, моделирование как EMD, так и rNEMD было выполнено для исследования тепловых свойств двух новых двумерных аллотропов углерода, состоящих из восьмиугольников и пятиугольников. Получено влияние размера, температуры и деформации на TC. Наши результаты показывают, что TC монотонно увеличивается с увеличением размера. Значения теплопроводности бесконечных размеров получаются линейными зависимостями обратной длины и обратной TC. Сведенная TC, полученная экстраполяцией в методе обратной неравновесной молекулярной динамики, находится в разумном согласии с таковой в методе равновесной молекулярной динамики. Значительно меньшая TC по сравнению с графеном объясняется меньшей групповой скоростью фононов и их длиной свободного пробега. Наши результаты дают важную информацию о влиянии размера, температуры и деформации на теплопередающие свойства OPG-L и OPG-Z, а также указывают на потенциальные применения в устройствах управления температурой в областях микро / наноэлектроники.

Сокращения

558:

Пяти-пяти-восьмичленные кольца

OPG-L:

Восьмиугольник и пятиугольник-линия графена

OPG-Z:

Восьмиугольник и пятиугольник графен-зигзаг

rNEMD:

Reverse non-equilibrium molecular dynamics

TC:

Теплопроводность

VDOS:

Vibrational density of states