Последовательности гармонических фаз

В последнем разделе мы увидели, как 3-я гармоника и все ее целые кратные (вместе называемые тройными гармоники), генерируемые фундаментальными сигналами, сдвинутыми по фазе на 120 °, фактически синфазны друг с другом.

В трехфазной сети с частотой 60 Гц, где фазы A , B и C разделены на 120 °, кратные третьей гармоники этих частот (180 Гц) идеально совпадают по фазе друг с другом.

Это можно представить в графических терминах (рисунок ниже) и / или в математических терминах:

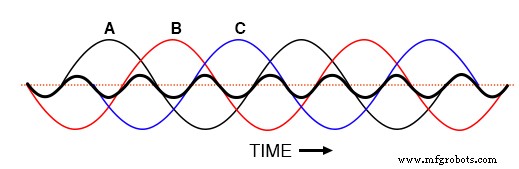
Гармонические токи фаз A, B, C совпадают, то есть вращения нет.

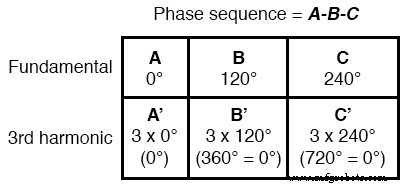
Расширенная математическая таблица с нечетными гармониками

Если мы расширим математическую таблицу, включив в нее высшие нечетные гармоники, мы заметим, что в отношении вращения или последовательности частот гармоник развивается интересная закономерность:

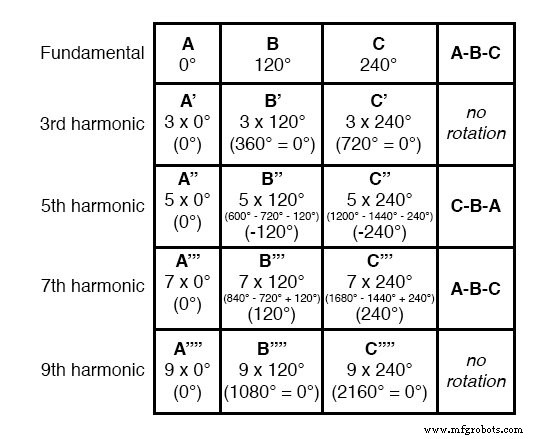
Гармоники, такие как 7-я, которые «вращаются» с той же последовательностью, что и основная, называются положительной последовательностью . .

Такие гармоники, как пятая, которые «вращаются» в последовательности, противоположной основной, называются отрицательной последовательностью . .

Тройные гармоники (3-я и 9-я показаны в этой таблице), которые вообще не «вращаются», потому что они находятся в фазе друг с другом, называются нулевой последовательностью . .

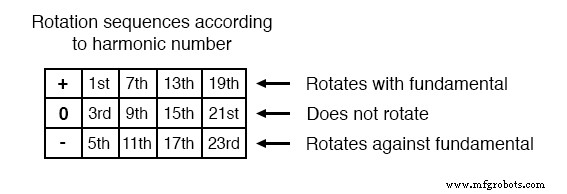
Этот паттерн положительный-ноль-отрицательный-положительный продолжается бесконечно для всех нечетных гармоник, поддающийся выражению в такой таблице:

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица сигналов смешанной частоты