Мощность в резистивных и реактивных цепях переменного тока

Рассмотрим схему для однофазной системы питания переменного тока, в которой источник переменного напряжения 120 В, 60 Гц подает питание на резистивную нагрузку:(рисунок ниже)

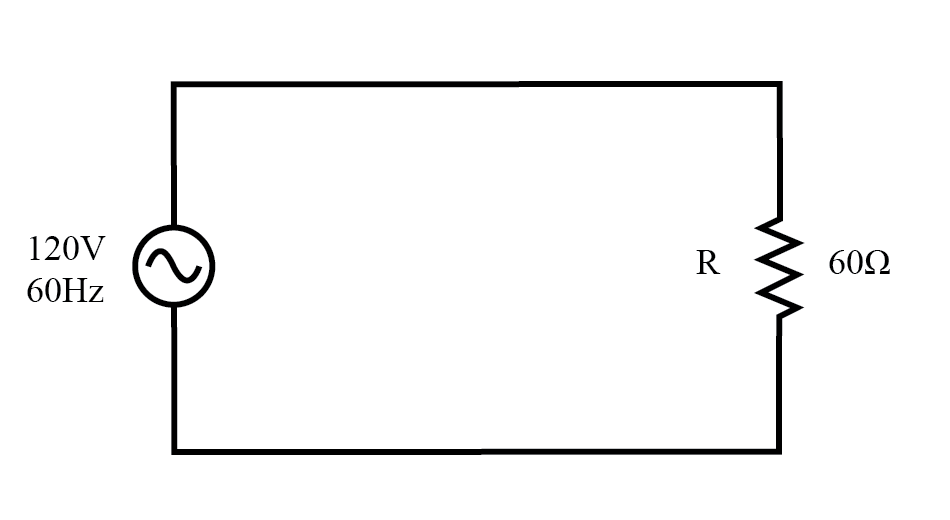
Источник переменного тока управляет чисто резистивной нагрузкой.

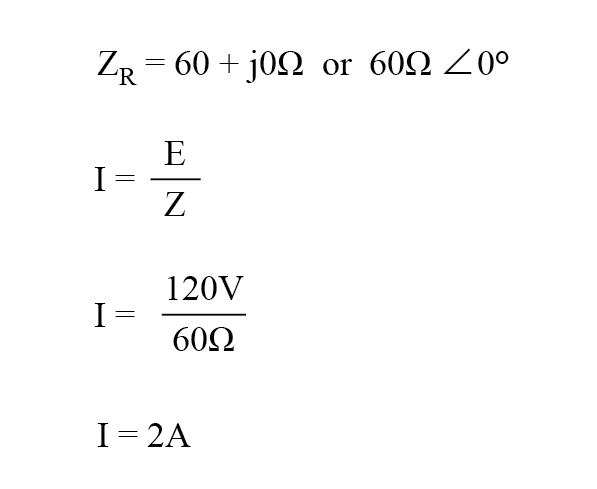
В этом примере ток нагрузки будет 2 ампера, среднеквадратичное значение. Мощность, рассеиваемая на нагрузке, составит 240 Вт.

Поскольку эта нагрузка является чисто резистивной (без реактивного сопротивления), ток находится в фазе с напряжением, и расчеты выглядят аналогично расчетам в эквивалентной цепи постоянного тока.

Если бы мы изобразили кривые напряжения, тока и мощности для этой схемы, это выглядело бы так, как показано на рисунке ниже.

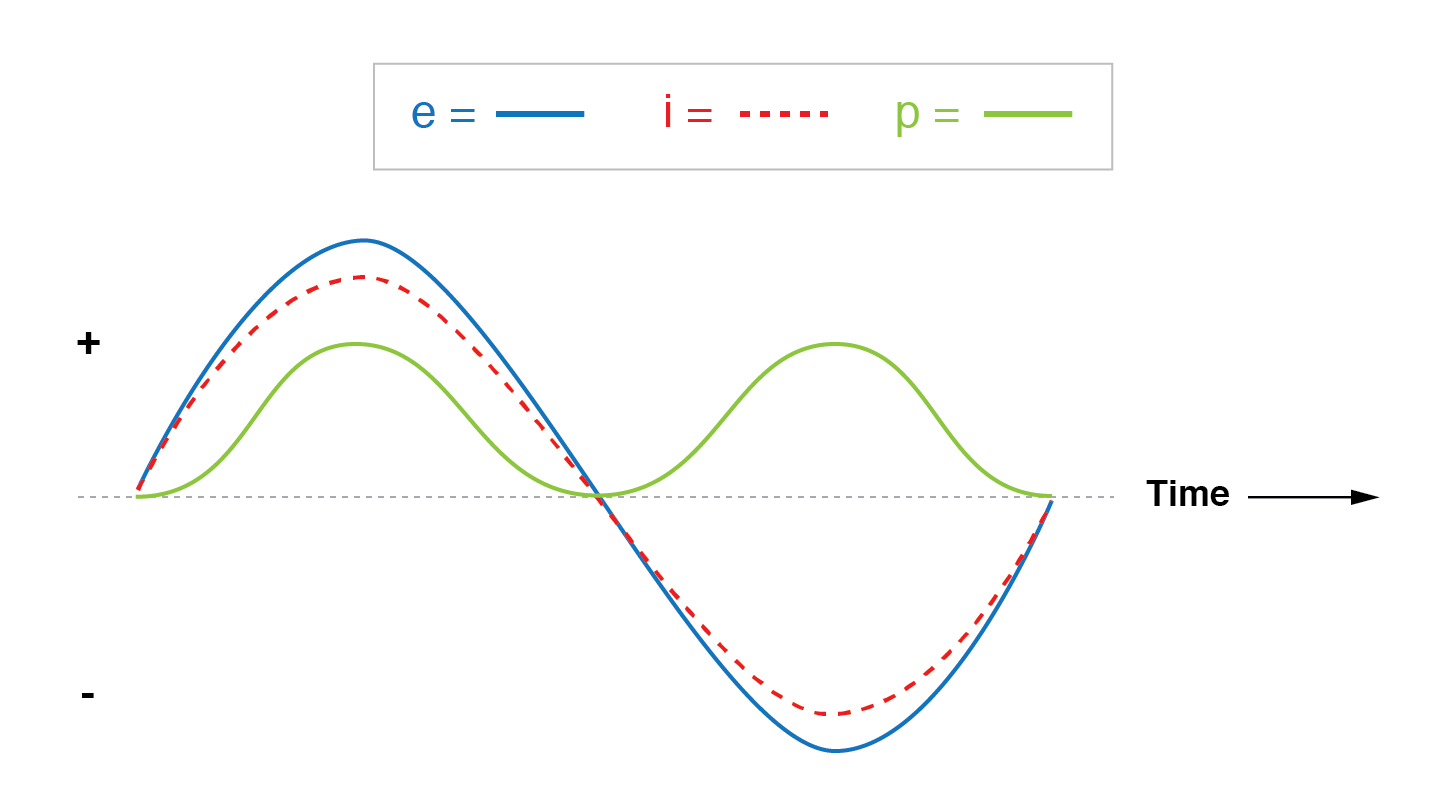
Ток в фазе с напряжением в резистивной цепи.

Обратите внимание, что форма сигнала мощности всегда положительна, а не отрицательна для этой резистивной цепи.

Это означает, что мощность всегда рассеивается резистивной нагрузкой и никогда не возвращается к источнику, как это происходит с реактивными нагрузками. Если бы источником был механический генератор, для поворота вала потребовалось бы 240 Вт механической энергии (около 1/3 лошадиных сил).

Также обратите внимание, что форма сигнала мощности не соответствует частоте напряжения или тока! Скорее, его частота двойная формы сигнала напряжения или тока.

Эта другая частота запрещает выражение мощности в цепи переменного тока с использованием тех же сложных (прямоугольных или полярных) обозначений, которые используются для напряжения, тока и импеданса, потому что эта форма математического символизма подразумевает неизменные фазовые отношения.

Когда частоты не совпадают, фазовые отношения постоянно меняются.

Как ни странно это может показаться, лучший способ продолжить расчеты мощности переменного тока - использовать скаляр обозначение и обрабатывать любые соответствующие фазовые отношения с помощью тригонометрии.

Цепь переменного тока с чисто реактивной нагрузкой

Для сравнения рассмотрим простую цепь переменного тока с чисто реактивной нагрузкой на рисунке ниже.

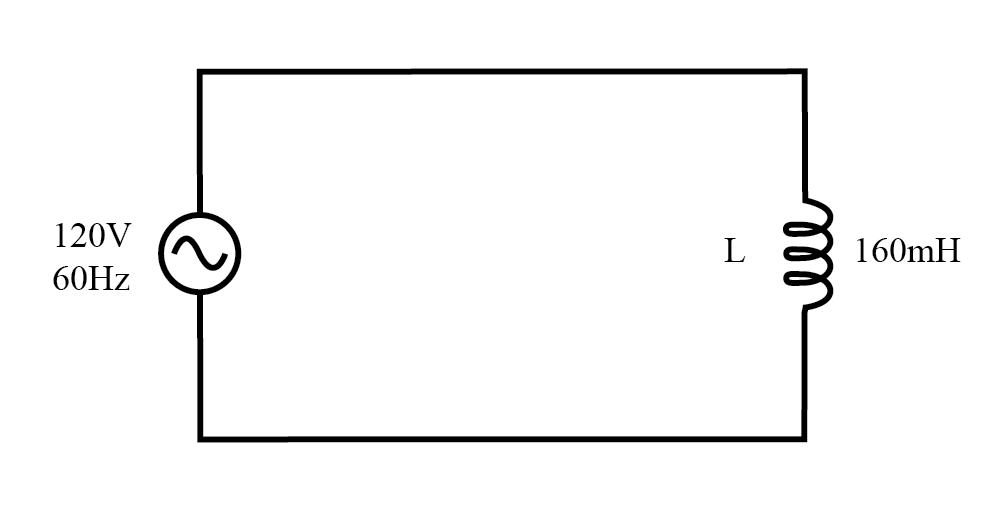
Схема переменного тока с чисто реактивной (индуктивной) нагрузкой.

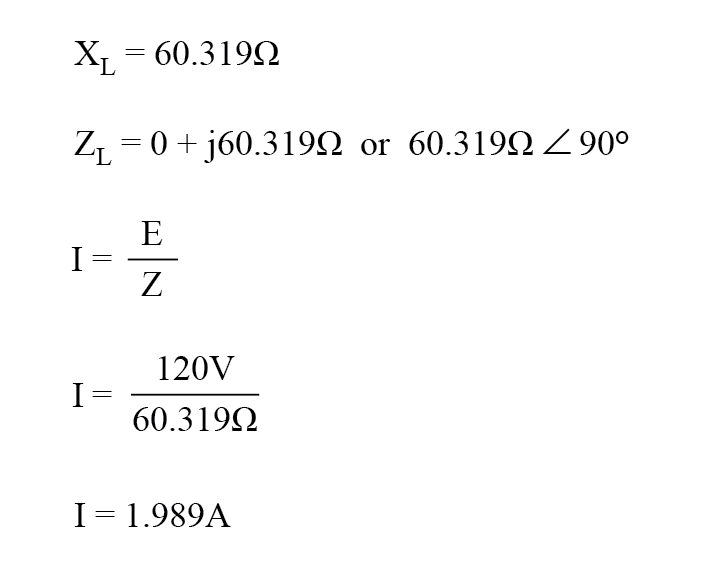
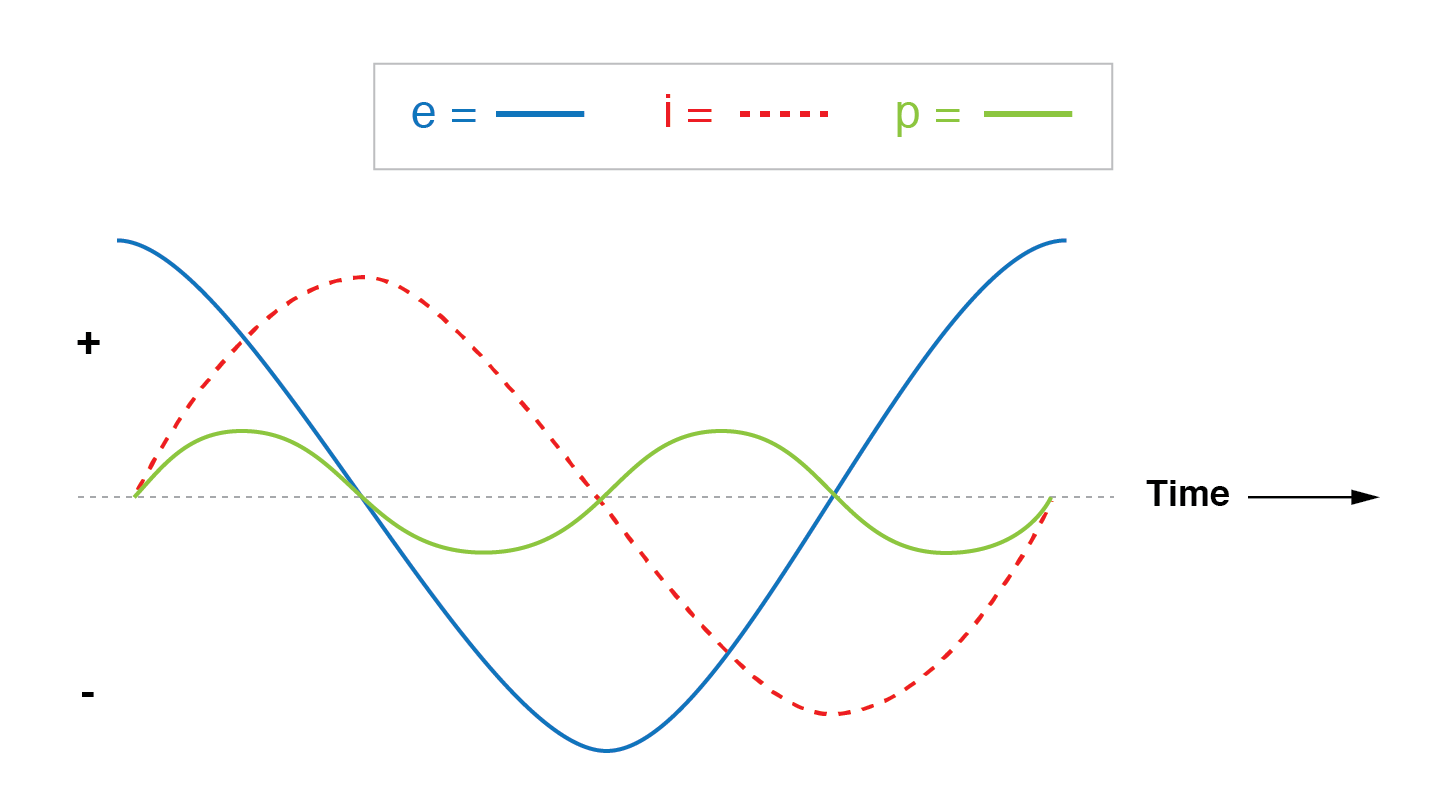
Мощность не рассеивается чисто реактивной нагрузкой. Хотя он попеременно поглощается источником и возвращается обратно.

Обратите внимание, что мощность одинаково чередуется между положительными и отрицательными циклами. (Рисунок выше) Это означает, что мощность поочередно поглощается и возвращается к источнику.

Если бы источником был механический генератор, для поворота вала не потребовалось бы (практически) никакой полезной механической энергии, потому что нагрузка не использовала бы никакой энергии.

Вал генератора будет легко вращаться, а индуктор не будет нагреваться, как резистор.

Цепь переменного тока с резистивной и чисто реактивной нагрузкой

Теперь давайте рассмотрим цепь переменного тока с нагрузкой, состоящей из индуктивности и сопротивления, как показано на рисунке ниже.

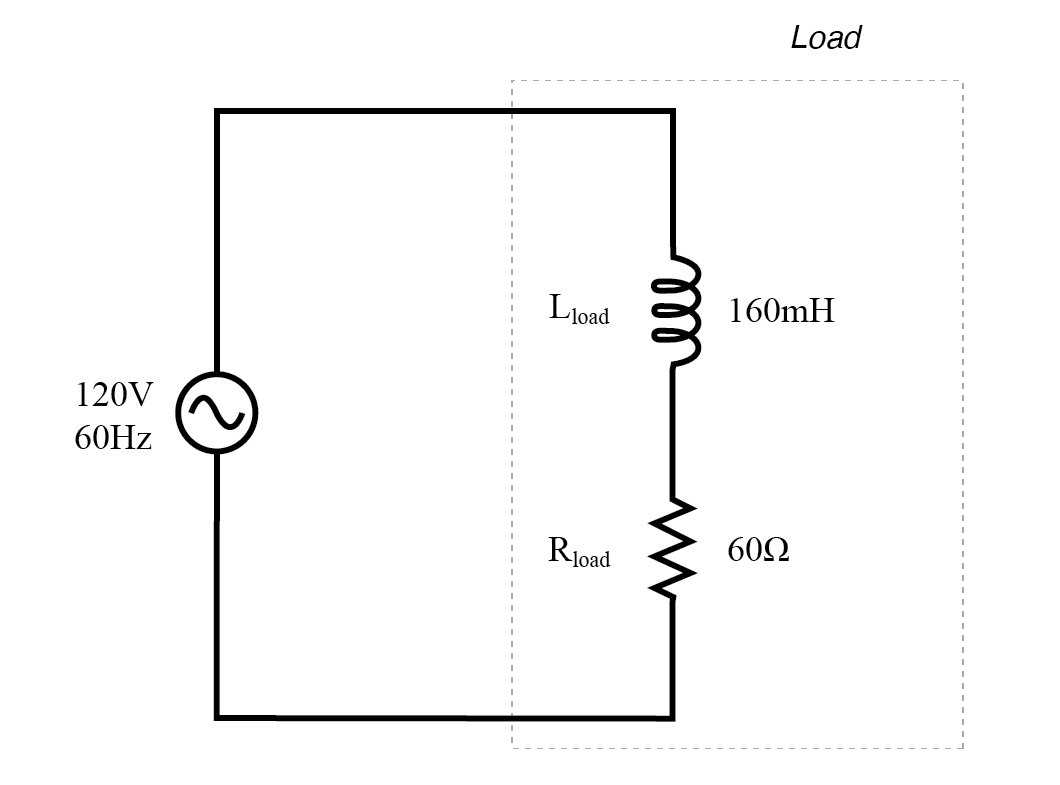
Цепь переменного тока с реактивным сопротивлением и сопротивлением.

На частоте 60 Гц индуктивность 160 миллигенри дает нам индуктивное реактивное сопротивление 60,319 Ом.

Это реактивное сопротивление в сочетании с сопротивлением 60 Ом образует полное сопротивление нагрузки 60 + j60,319 Ом, или 85,078 Ом 45,152 ^o . . Если нас не интересуют фазовые углы (чего мы еще не достигли), мы можем рассчитать ток в цепи, взяв полярную величину источника напряжения (120 вольт) и разделив ее на полярную величину импеданса. (85,078 Ом).

При напряжении источника питания 120 вольт RMS ток нагрузки составляет 1,410 ампер. Это значение, которое показывает амперметр RMS, если он подключен последовательно с резистором и катушкой индуктивности.

Мы уже знаем, что реактивные компоненты рассеивают нулевую мощность, поскольку они в равной степени поглощают мощность и возвращают мощность в остальную часть схемы.

Следовательно, любое индуктивное реактивное сопротивление в этой нагрузке также будет рассеивать нулевую мощность.

Единственное, что здесь осталось для рассеивания мощности, - это резистивная часть импеданса нагрузки. Если мы посмотрим на график формы волны напряжения, тока и полной мощности для этой схемы, мы увидим, как эта комбинация работает на рисунке ниже.

Комбинированная резистивная / реактивная цепь рассеивает больше энергии, чем возвращается к источнику. Реактивное сопротивление не рассеивает мощность; хотя резистор работает.

Как и в любой реактивной схеме, мощность со временем меняется между положительными и отрицательными мгновенными значениями.

В чисто реактивной схеме чередование положительной и отрицательной мощности делится поровну, в результате чего рассеиваемая полезная мощность равна нулю. Однако в схемах со смешанным сопротивлением и реактивным сопротивлением, подобных этой, форма волны мощности по-прежнему будет чередоваться между положительной и отрицательной, но количество положительной мощности будет превышать количество отрицательной мощности.

Другими словами, комбинированная индуктивная / резистивная нагрузка потребляет больше энергии, чем возвращается к источнику.

Глядя на график формы волны для мощности, должно быть очевидно, что волна проводит больше времени на положительной стороне центральной линии, чем на отрицательной, что указывает на то, что нагрузка потребляет больше мощности, чем возвращается в цепь. P>

То небольшое возвращение мощности происходит из-за реактивного сопротивления; дисбаланс положительной и отрицательной мощности связан с сопротивлением, поскольку она рассеивает энергию за пределами цепи (обычно в виде тепла).

Если бы источником был механический генератор, количество механической энергии, необходимое для вращения вала, было бы суммой мощности, усредненной между положительным и отрицательным циклами мощности.

Математическое представление мощности в цепи переменного тока является сложной задачей, потому что волна мощности не имеет той же частоты, что и напряжение или ток.

Кроме того, фазовый угол для мощности означает нечто совершенно иное, чем фазовый угол для напряжения или тока. В то время как угол для напряжения или тока представляет относительный сдвиг во времени между двумя волнами фазовый угол мощности представляет собой соотношение между рассеиваемой и возвращаемой мощностью.

Из-за того, что мощность переменного тока отличается от напряжения или тока переменного тока, на самом деле легче получить значения мощности, вычисляя с помощью скаляра величины напряжения, тока, сопротивления и реактивного сопротивления, чем нужно попытаться получить из вектора , или сложный величины напряжения, тока и сопротивления, с которыми мы работали до сих пор.

ОБЗОР:

• В чисто резистивной схеме вся мощность схемы рассеивается резисторами. Напряжение и ток синфазны.
• В чисто реактивной схеме мощность не рассеивается нагрузкой (ами). Напротив, мощность поочередно поглощается и возвращается к источнику переменного тока. Напряжение и ток сдвинуты по фазе на 90 °.
• В цепи, состоящей из смешанного сопротивления и реактивного сопротивления, мощность, рассеиваемая нагрузкой (ами), будет больше, чем возвращаемая, но некоторая мощность определенно будет рассеиваться, а некоторая будет просто поглощаться и возвращаться. Напряжение и ток в такой цепи будут сдвинуты по фазе на величину где-то между 0 ° и 90 °.

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Таблица мощности переменного тока