Гармоники в многофазных системах питания

В главе, посвященной сигналам со смешанной частотой, мы исследовали концепцию гармоник . в системах переменного тока:частоты, кратные основной частоте источника.

В системах питания переменного тока, в которых форма волны напряжения источника, поступающего от генератора переменного тока (генератора переменного тока), должна быть одночастотной синусоидальной волной, неискаженной, не должно быть гармонических составляющих. . . в идеале.

Нелинейные компоненты в системах переменного тока

Это было бы верно, если бы не нелинейные компоненты . Нелинейные компоненты потребляют ток непропорционально напряжению источника, вызывая несинусоидальные формы волны тока.

Примеры нелинейных компонентов включают газоразрядные лампы, полупроводниковые устройства управления мощностью (диоды, транзисторы, тиристоры, симисторы тока), трансформаторы (ток намагничивания первичной обмотки обычно не является синусоидальным из-за кривой насыщения сердечника B / H) и электродвигатели (опять же, когда магнитные поля в сердечнике двигателя работают почти на уровне насыщения).

Даже лампы накаливания генерируют слегка несинусоидальные токи, поскольку сопротивление нити накала изменяется на протяжении всего цикла из-за быстрых колебаний температуры.

Как мы узнали из главы, посвященной смешанной частоте, любой искажение формы волны синусоиды, иначе говоря, означает наличие гармонических частот.

Когда рассматриваемая несинусоидальная форма волны симметрична выше и ниже ее средней центральной линии, частоты гармоник будут нечетными целыми числами, кратными только основной частоте источника, без четных целых кратных.

Большинство нелинейных нагрузок создают такие формы тока, поэтому четные гармоники (2-я, 4-я, 6-я, 8-я, 10-я, 12-я и т. Д.) Отсутствуют или присутствуют минимально в большинстве систем переменного тока.

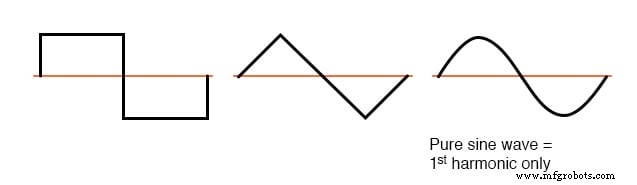
Примеры симметричных сигналов - только нечетные гармоники.

Примеры несимметричных сигналов с присутствующими четными гармониками показаны для справки на рисунке ниже.

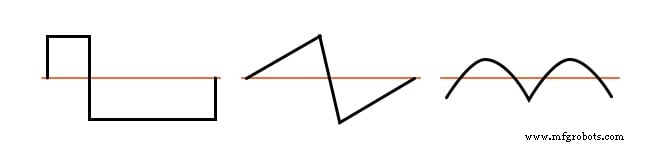
Примеры несимметричных сигналов - присутствуют даже гармоники.

Несмотря на то, что половина возможных частот гармоник устраняется обычно симметричным искажением нелинейных нагрузок, нечетные гармоники все же могут вызывать проблемы. Некоторые из этих проблем являются общими для всех энергосистем, однофазных или иных.

Например, перегрев трансформатора из-за потерь на вихревые токи может произойти в любом Система питания переменного тока со значительным содержанием гармоник.

Однако существуют некоторые проблемы, вызванные гармоническими токами, характерными для многофазных систем питания, и именно этим проблемам специально посвящен этот раздел.

Моделирование гармонических эффектов SPICE

Полезно иметь возможность моделировать нелинейные нагрузки в SPICE, чтобы избежать большого количества сложной математики и получить более интуитивное понимание гармонических эффектов.

Моделирование линейной системы переменного тока

Сначала мы начнем моделирование с очень простой цепи переменного тока:одиночного источника синусоидального напряжения с чисто линейной нагрузкой и всеми соответствующими сопротивлениями:

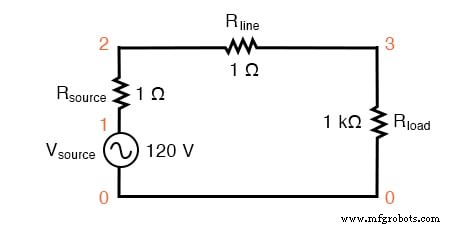
Схема SPICE с одним источником синусоидальной волны.

Источник R и R _line Сопротивления в этой цепи не просто имитируют реальный мир:они также обеспечивают удобные шунтирующие сопротивления для измерения токов в моделировании SPICE:считывая напряжение на сопротивлении 1 Ом, вы получаете прямую индикацию тока через него, поскольку E =IR .

Моделирование этой схемы SPICE (список SPICE:«моделирование линейной нагрузки») с анализом Фурье по напряжению, измеренному на R _линии должен показать нам содержание гармоник в линейном токе этой схемы. Поскольку мы полностью линейны по своей природе, мы не должны ожидать никаких гармоник, кроме 1-й (основной) частоты 60 Гц, если предположить, что источник 60 Гц.

См. Выходные данные SPICE «Фурье-компоненты переходной характеристики v (2,3)» и рисунок ниже.

 моделирование линейной нагрузки vsource 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k .options itl5 =0 .tran 0,5 м 30 м 0 1 ед. .plot tran v (2,3) . четыре 60 v (2,3) .конец 

 Фурье-компоненты переходной характеристики v (2,3) компонент постоянного тока =4.028E-12 частота гармоник, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 5.793E-12 0.000000 51.122 123.122 3 1,800E + 02 7,407E-12 0,000000 -34,624 37,376 4 2.400E + 02 9.056E-12 0.000000 4.267 76.267 5 3.000E + 02 1.651E-11 0.000000 -83.461 -11.461 6 3.600E + 02 3.931E-11 0.000000 36.399 108.399 7 4.200E + 02 2.338E-11 0.000000 -41.343 30.657 8 4.800E + 02 4.716E-11 0.000000 53.324 125.324 9 5.400E + 02 3.453E-11 0.000000 21.691 93.691 общее гармоническое искажение =0,000000 процента 

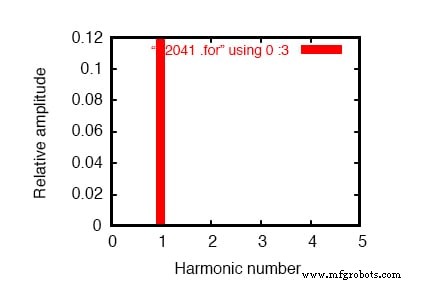
График в частотной области одночастотного компонента. См. Список SPICE:«Моделирование линейной нагрузки».

Команда .plot появляется в списке соединений SPICE, и обычно это приводит к выводу синусоидального графика. В данном случае, однако, для краткости я намеренно опустил отображение формы сигнала - команда .plot находится в списке соединений просто для того, чтобы удовлетворить причуду функции преобразования Фурье SPICE.

Никакое дискретное преобразование Фурье не является совершенным, и поэтому мы видим очень маленькие гармонические токи, указанные (в диапазоне пико-ампер!) Для всех частот вплоть до 9-й гармоники (в таблице), что соответствует уровню SPICE при выполнении анализа Фурье. .

Мы показываем 0,1198 ампер (1.198E-01) для «Фурье-составляющей» 1-й гармоники или основной частоты, которая является нашим ожидаемым током нагрузки:около 120 мА, при напряжении источника 120 В и сопротивлении нагрузки 1 кОм.

Простое нелинейное моделирование однофазной системы переменного тока

Затем я хотел бы смоделировать нелинейную нагрузку, чтобы генерировать гармонические токи. Это можно сделать двумя принципиально разными способами. Один из способов - спроектировать нагрузку с использованием нелинейных компонентов, таких как диоды или другие полупроводниковые устройства, которые легко моделировать с помощью SPICE. Другой - добавить несколько источников переменного тока параллельно нагрузочному резистору.

Инженеры часто предпочитают последний метод для моделирования гармоник, поскольку источники тока известного значения лучше подходят для математического анализа сети, чем компоненты с очень сложными характеристиками отклика.

Поскольку мы позволяем SPICE выполнять всю математическую работу, сложность полупроводникового компонента не вызовет для нас проблем, но, поскольку источники тока можно точно настроить для получения любой произвольной величины тока (удобная функция), я выберите последний подход, показанный на рисунке ниже и в списке SPICE «Нелинейное моделирование нагрузки».

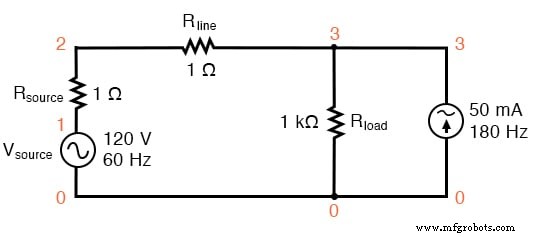
Схема SPICE:источник 60 Гц с добавленной третьей гармоникой.

 Нелинейное моделирование нагрузки vsource 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) .options itl5 =0 .tran 0,5 м 30 м 0 1 ед. .plot tran v (2,3) . четыре 60 v (2,3) .конец 

В этой схеме у нас есть источник тока величиной 50 мА и частотой 180 Гц, что в три раза превышает частоту источника 60 Гц. При подключении параллельно нагрузочному резистору 1 кОм его ток складывается с током резистора, чтобы получить несинусоидальный общий линейный ток.

Я покажу график формы волны на рисунке ниже, чтобы вы могли увидеть влияние этой 3-й гармоники тока на общий ток, который обычно был бы простой синусоидой.

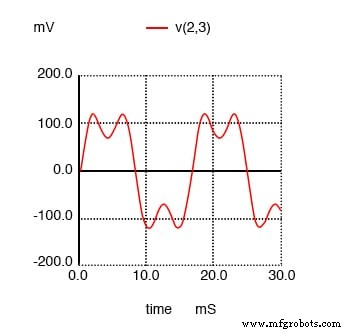
График SPICE во временной области, показывающий сумму источника 60 Гц и 3-й гармоники 180 Гц.

 Фурье-компоненты переходной характеристики v (2,3) составляющая постоянного тока =1,349E-11 частота гармоник, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.609E-11 0,000000 67,570 139,570 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E + 02 3.871E-11 0.000000 169.582 241.582 6 3.600E + 02 5.736E-11 0.000000 140.845 212.845 7 4.200E + 02 8.407E-11 0.000000 177.071 249.071 8 4.800E + 02 1.329E-10 0.000000 156.772 228.772 9 5.400E + 02 2.619E-10 0.000000 160.498 232.498 общее гармоническое искажение =41,666663 процента 

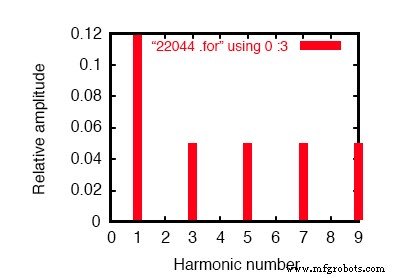
График Фурье SPICE, показывающий источник 60 Гц и 3-ю гармонику 180 Гц.

В анализе Фурье (см. Рисунок выше и «Фурье-компоненты переходной характеристики v (2,3)») смешанные частоты не смешиваются и представляются отдельно.

Здесь мы видим те же 0,1198 ампер тока 60 Гц (основной гармоники), что и в первом моделировании, но в строке 3-й гармоники мы видим 49,9 мА:наш источник тока 50 мА, 180 Гц в действии. Почему мы не видим через линию все 50 мА?

Поскольку этот источник тока подключен к нагрузочному резистору 1 кОм, некоторые из его токов шунтируются через нагрузку и никогда не проходят через линию обратно к источнику. Это неизбежное следствие моделирования такого типа, когда одна часть нагрузки является «нормальной» (резистор), а другая часть имитируется источником тока.

Моделирование нелинейной однофазной системы переменного тока с несколькими источниками тока

Если бы мы добавили больше источников тока к «нагрузке», мы бы увидели дальнейшее искажение формы волны линейного тока от идеальной синусоидальной формы, и каждая из этих гармонических токов появилась бы в пробое Фурье-анализа. См. Рисунок ниже и список SPICE:«Моделирование нелинейной нагрузки».

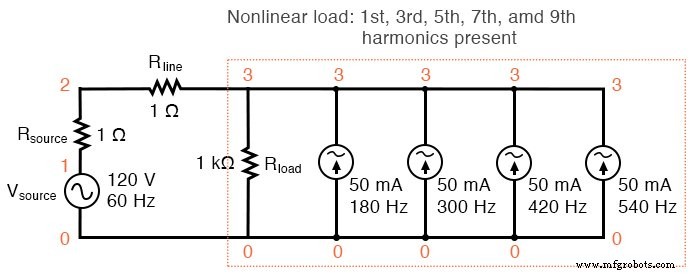
Нелинейная нагрузка:присутствуют 1-я, 3-я, 5-я, 7-я и 9-я гармоники.

 Моделирование нелинейной нагрузки vsource 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) i5har 3 0 грех (0 50 м 300 0 0) i7har 3 0 sin (0 50 м 420 0 0) i9har 3 0 sin (0 50m 540 0 0) .options itl5 =0 .tran 0,5 м 30 м 0 1 ед. .plot tran v (2,3) . четыре 60 v (2,3). конец 

 Фурье-компоненты переходной характеристики v (2,3) компонент постоянного тока =6,299E-11 частота гармоник, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.900E-09 0,000000 -93,908 -21,908 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E + 02 4.990E-02 0.416667 0.000 72.000 6 3.600E + 02 6.271E-09 0.000000 85.062 157.062 7 4.200E + 02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E + 02 2.742E-09 0.000000 -38.781 33.219 9 5.400E + 02 4.990E-02 0.416666 72.000 144.000 общее гармоническое искажение =83,333296 процентов 

Анализ Фурье:«Фурье-компоненты переходной характеристики v (2,3)».

Как видно из анализа Фурье (рисунок выше), каждый источник гармонического тока одинаково представлен в линейном токе, по 49,9 мА каждый. Пока что это просто моделирование однофазной энергосистемы.

Моделирование трехфазной системы переменного тока

Все становится еще интереснее, когда мы делаем трехфазное моделирование. Будут выполнены два анализа Фурье:один для напряжения на линейном резисторе, а второй - для напряжения на нейтральном резисторе.

Как и раньше, считывание значений напряжений на фиксированных сопротивлениях в 1 Ом каждое дает прямые показания тока, протекающего через эти резисторы. См. Рисунок ниже и список SPICE «4-проводная система источника / нагрузки Y-Y с гармониками».

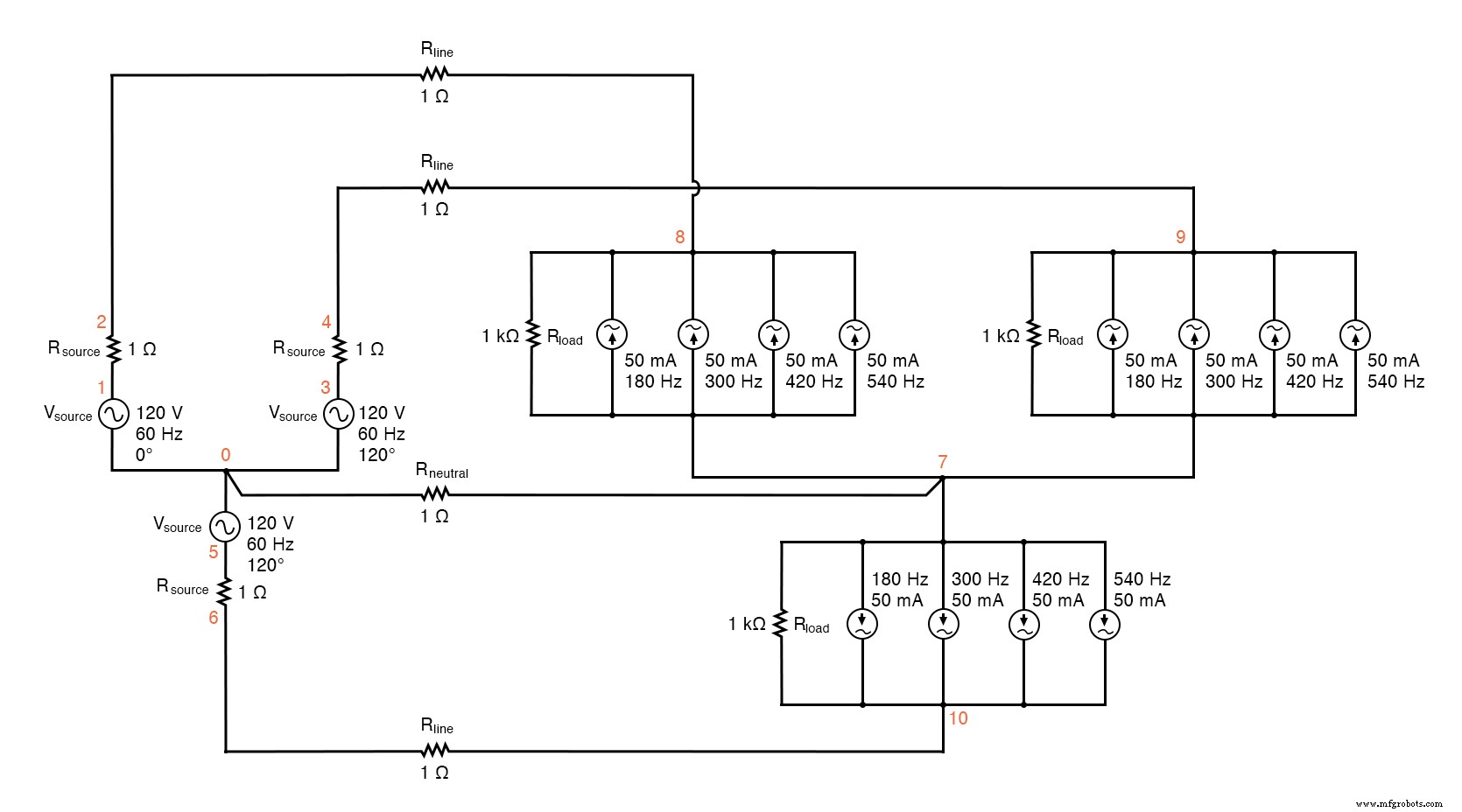
Схема SPICE:анализ «линейного тока» и «тока нейтрали», 4-проводная система источника / нагрузки Y-Y с гармониками.

 Y-Y источник / нагрузка 4-проводная система с гармониками * * источник напряжения фазы 1 и r (120 В / _ 0 градусов) vsource1 1 0 sin (0120 60 0 0) rsource1 1 2 1 * * источник напряжения фазы 2 и r (120 В / _ 120 град) vsource2 3 0 sin (0120 60 5.55555m 0) rsource2 3 4 1 * * источник напряжения фазы 3 и r (120 В / _ 240 градусов) vsource3 5 0 sin (0120 60 11,1111m 0) rsource3 5 6 1 * * сопротивление линии и нейтрали rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 р нейтральный 0 7 1 * * фаза 1 нагрузки rload1 8 7 1k i3har1 8 7 sin (0 50m 180 0 0) i5har1 8 7 sin (0 50m 300 0 0) i7har1 8 7 sin (0 50м 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * фаза 2 нагрузки rload2 9 7 1k i3har2 9 7 sin (0 50 м 180 5,55555 м 0) i5har2 9 7 sin (0 50 м 300 5,55555 м 0) i7har2 9 7 sin (0 50 м 420 5,55555 м 0) i9har2 9 7 sin (0 50 м 540 5,55555 м 0) * * фаза 3 нагрузки rload3 10 7 1k i3har3 10 7 sin (0 50 м 180 11,1111 м 0) i5har3 10 7 sin (0 50 м 300 11,1111 м 0) i7har3 10 7 sin (0 50 м 420 11,1111 м 0) i9har3 10 7 sin (0 50 м 540 11,1111 м 0) * * аналитические материалы .options itl5 =0 .tran 0.5м 100м 12м 1у .plot tran v (2,8) четыре 60 в (2,8) .plot tran v (0,7) четыре 60 В (0,7) .конец 

Фурье-анализ линейного тока:

 Фурье-компоненты переходной характеристики v (2,8) компонент постоянного тока =-6,404E-12 частота гармоник, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 6.000E + 01 1.198E-01 1.000000 0.000 0.000 2 1.200E + 02 2.218E-10 0,000000 172,985 172,985 3 1.800E + 02 4.975E-02 0.415423 0.000 0.000 4 2.400E + 02 4.236E-10 0.000000 166.990 166.990 5 3.000E + 02 4.990E-02 0.416667 0.000 0.000 6 3.600E + 02 1.877E-10 0.000000 -147.146 -147.146 7 4.200E + 02 4.990E-02 0.416666 0.000 0.000 8 4.800E + 02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E + 02 4.975E-02 0.415422 0.000 0.000 общее гармоническое искажение =83,209009 процентов 

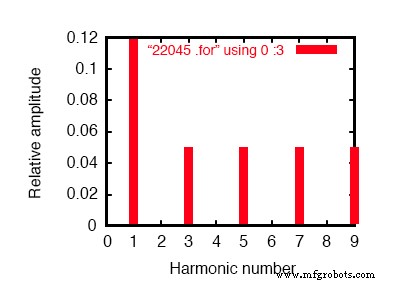
Фурье-анализ линейного тока в сбалансированной системе Y-Y .

Фурье-анализ нейтрального тока:

 Фурье-компоненты переходной характеристики v (0,7) составляющая постоянного тока =1,819E-10 частота гармоник, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 6.000E + 01 4.337E-07 1.000000 60.018 0.000 2 1.200E + 02 1.869E-10 0.000431 91.206 31.188 3 1.800E + 02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E + 02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E + 02 9.023E-07 2.080596 119.981 59.963 6 3.600E + 02 3.396E-10 0.000783 15.882 -44.136 7 4.200E + 02 1.264E-06 2.913955 59.993 -0.025 8 4.800E + 02 5.975E-10 0.001378 35.584 -24.434 9 5.400E + 02 1.493E-01 344147.4889 -179.999 -240.017 

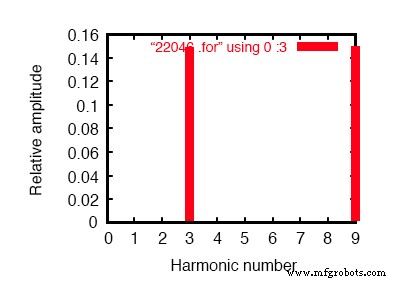
Фурье-анализ нейтрального тока показывает, что кроме гармоник нет! Сравните с линейным током на рисунке выше.

Это сбалансированная система питания Y-Y, каждая фаза которой идентична однофазной системе переменного тока, смоделированной ранее. Следовательно, неудивительно, что анализ Фурье для линейного тока в одной фазе трехфазной системы почти идентичен анализу Фурье для линейного тока в однофазной системе:основной (60 Гц) линейный ток 0,1198 ампер и токи нечетных гармоник примерно 50 мА каждый.

См. Рисунок выше и анализ Фурье:«Фурье-компоненты переходной характеристики v (2,8)»

Что должно удивить здесь, так это анализ тока нейтрального проводника, который определяется падением напряжения на R _{нейтрали} . резистор между узлами SPICE 0 и 7.

В сбалансированной трехфазной нагрузке Y мы ожидаем, что ток нейтрали будет равен нулю. Каждый фазный ток, который сам по себе будет проходить через нейтральный провод обратно к фазе питания на источнике Y, должен нейтрализовать друг друга по отношению к нейтральному проводнику, потому что все они одинаковой величины и все смещены на 120 ° друг от друга. P>

В системе без гармонических токов это равно что происходит, оставляя нулевой ток через нейтральный провод.

Эффекты гармонических токов в системе

Однако мы не можем сказать то же самое о гармоническом токи в одной системе.

Обратите внимание, что ток основной частоты (60 Гц или 1-я гармоника) практически отсутствует в нейтральном проводе. Наш анализ Фурье показывает только 0,4337 мкА первой гармоники при считывании напряжения на R _{нейтрали} . . То же самое можно сказать о 5-й и 7-й гармониках, оба из которых имеют незначительную величину.

Напротив, 3-я и 9-я гармоники сильно представлены в нейтральном проводе, с 149,3 мА (1,493E-01 вольт на 1 Ом) каждая! Это почти 150 мА, или в три раза больше значений источников тока по отдельности.

С тремя источниками на каждую гармоническую частоту в нагрузке, кажется, что наши токи 3-й и 9-й гармоник в каждой фазе складываются чтобы сформировать нейтральный ток. См. Анализ Фурье:«Фурье-компоненты переходной характеристики v (0,7)»

Анализ графиков во временной области

Именно это и происходит, хотя может быть непонятно, почему это так.

Ключ к пониманию этого явствует из графика фазовых токов во временной области. Изучите этот график сбалансированных фазных токов во времени с последовательностью фаз 1-2-3. (Рисунок ниже)

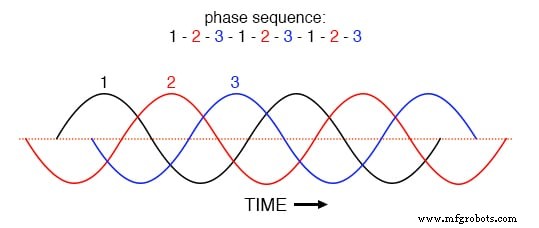
Последовательность фаз 1-2-3-1-2-3-1-2-3 равномерно распределенных волн.

С тремя основными формами сигналов, одинаково смещенными по временной оси графика, легко увидеть, как они компенсируют друг друга, давая результирующий нулевой ток в нейтральном проводнике. Однако давайте посмотрим, как будет выглядеть сигнал третьей гармоники для фазы 1, наложенный на график на рисунке ниже.

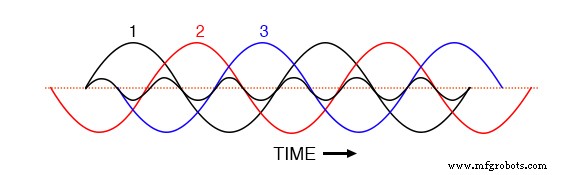
Форма волны третьей гармоники для фазы 1, наложенная на формы волны трехфазной основной частоты.

Обратите внимание на то, как эта гармоническая форма волны имеет такое же фазовое соотношение со 2-й и 3-ей основными формами волны, как и с 1-й:в каждом положительном полупериоде any Из основных сигналов вы найдете ровно два положительных полупериода и один отрицательный полупериод гармонической формы волны.

Это означает, что формы сигналов третьей гармоники трех сигналов основной частоты, сдвинутых по фазе на 120 °, на самом деле синфазны друг с другом. Значение фазового сдвига 120 °, обычно принимаемое в трехфазных системах переменного тока, применяется только к основным частотам, а не к их гармоническим кратным!

Если бы мы изобразили все три формы сигнала третьей гармоники на одном графике, мы бы увидели, что они точно перекрываются и отображались бы как единый унифицированный сигнал (выделенный жирным шрифтом (рисунок ниже)

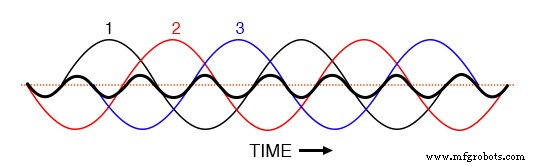
Третьи гармоники для фаз 1, 2, 3 все совпадают при наложении на основные трехфазные сигналы.

Математический анализ графика во временной области

Для более склонных к математике этот принцип может быть выражен символически. Предположим, что A представляет одну форму волны, а B другой, оба на той же частоте, но сдвинутые на 120 ° друг от друга по фазе. Назовем третью гармонику каждого сигнала A ’. и B ’ соответственно.

Фазовый сдвиг между A ’ и B ’ не 120 ° (это фазовый сдвиг между A и B ), но в 3 раза больше, потому что A ’ и B ’ формы волны чередуются в три раза быстрее, чем A и B . Сдвиг между формами сигналов точно выражается только в терминах фазового угла . когда предполагается такая же угловая скорость.

При связывании форм сигналов с разной частотой наиболее точный способ представления фазового сдвига - это время .; и сдвиг во времени между A ’ и B ’ эквивалентно 120 ° при частоте в три раза меньшей или 360 ° при частоте A ’ и B ’ . Фазовый сдвиг на 360 ° совпадает с фазовым сдвигом на 0 °, то есть без фазового сдвига вообще.

Таким образом, A ’ и B ’ должны совпадать по фазе друг с другом:

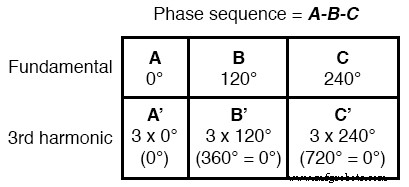
Эта характеристика 3-й гармоники в трехфазной системе также верна для любых целых кратных 3-й гармоники.

Таким образом, не только 3-я гармоника каждой основной формы волны находится в фазе друг с другом, но также 6-я гармоника, 9-я гармоника, 12-я гармоника, 15-я гармоника, 18-я гармоника, 21-я гармоника и так далее.

Поскольку только нечетные гармоники появляются в системах, в которых искажение формы волны симметрично относительно центральной линии, а большинство нелинейных нагрузок создают симметричное искажение, четные кратные 3-й гармоники (6-я, 12-я, 18-я и т. Д.), Как правило, не имеют значения, оставляя только кратные числа с нечетным номером (3-й, 9-й, 15-й, 21-й и т. д.), чтобы вносить существенный вклад в токи нейтрали.

В многофазных энергосистемах с некоторым количеством фаз, отличным от трех, этот эффект возникает с гармониками того же кратного значения. Например, гармонические токи, которые добавляют в нейтральный проводник 4-фазной системы, соединенной звездой, где фазовый сдвиг между основными формами волны составляет 90 °, будут 4-й, 8-й, 12-й, 16-й, 20-й и т. Д. P>

Тройные гармоники

Из-за большого количества и значимости в трехфазных энергосистемах 3-я гармоника и ее кратные имеют собственное особое название: тройные гармоники .

Все тройные гармоники складываются друг с другом в нейтральном проводе 4-проводной нагрузки с Y-соединением. В энергосистемах со значительной нелинейной нагрузкой тройные гармонические токи могут иметь достаточно большую величину, чтобы вызвать перегрев нейтральных проводников.

Это очень проблематично, поскольку другие соображения безопасности не позволяют нейтральным проводникам иметь максимальную токовую защиту, и, таким образом, нет никаких условий для автоматического отключения этих высоких токов.

Анализ влияния тройных гармоник в цепи Y-Y

На следующем рисунке показано, как тройные гармонические токи, создаваемые нагрузкой, складываются в нейтральный проводник. Символ «ω» используется для обозначения угловой скорости и математически эквивалентен 2πf. Итак, «ω» представляет основную частоту, «3ω» представляет 3-ю гармонику, «5ω» представляет 5-ю гармонику и так далее:(рисунок ниже)

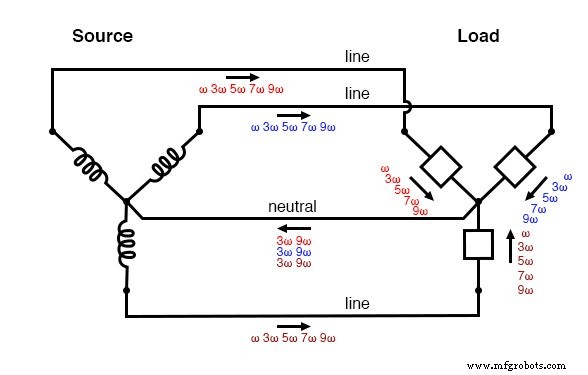
Тройной источник / нагрузка «Y-Y»:гармонические токи добавляются в нейтральный проводник.

In an effort to mitigate these additive triplen currents, one might be tempted to remove the neutral wire entirely. If there is no neutral wire in which triplen currents can flow together, then they won’t, right?

Unfortunately, doing so just causes a different problem:the load’s “Y” center-point will no longer be at the same potential as the source’s, meaning that each phase of the load will receive a different voltage than what is produced by the source.

We’ll re-run the last SPICE simulation without the 1 Ω R_neutral resistor and see what happens:

Y-Y source/load (no neutral) with harmonics * * phase1 voltage source and r (120 v / 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v / 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v / 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * line resistances rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 0 0) i5har1 8 7 sin(0 50m 300 0 0) i7har1 8 7 sin(0 50m 420 0 0) i9har1 8 7 sin(0 50m 540 0 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 12m 1u .plot tran v(2,8) .four 60 v(2,8) .plot tran v(0,7) .four 60 v(0,7) .plot tran v(8,7) .four 60 v(8,7) .конец 

Fourier analysis of line current:

Fourier components of transient response v(2,8) dc component =5.423E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.388E-10 0.000000 158.016 158.016 3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E+02 4.990E-02 0.416665 0.000 0.000 6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E+02 4.990E-02 0.416668 0.000 0.000 8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005 total harmonic distortion =58.925539 percent 

Fourier analysis of voltage between the two “Y” center-points:

Fourier components of transient response v(0,7) dc component =6.093E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.453E-04 1.000000 60.018 0.000 2 1.200E+02 6.263E-08 0.000431 91.206 31.188 3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018 4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E+02 3.023E-04 2.080596 119.981 59.963 6 3.600E+02 1.138E-07 0.000783 15.882 -44.136 7 4.200E+02 4.234E-04 2.913955 59.993 -0.025 8 4.800E+02 2.001E-07 0.001378 35.584 -24.434 9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017 total harmonic distortion =************ percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =6.070E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 0.000 0.000 2 1.200E+02 6.231E-08 0.000000 90.473 90.473 3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000 4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E+02 9.995E-02 0.000835 179.850 179.850 6 3.600E+02 1.023E-07 0.000000 13.485 13.485 7 4.200E+02 9.959E-02 0.000832 179.790 179.789 8 4.800E+02 1.991E-07 0.000000 35.462 35.462 9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999 total harmonic distortion =59.043467 percent 

Strange things are happening, indeed.

First, we see that the triplen harmonic currents (3rd and 9th) all but disappear in the lines connecting a load to source. The 5th and 7th harmonic currents are present at their normal levels (approximately 50 mA), but the 3rd and 9th harmonic currents are of negligible magnitude.

Second, we see that there is a substantial harmonic voltage between the two “Y” center-points, between which the neutral conductor used to connect. According to SPICE, there are 50 volts of both 3rd and 9th harmonic frequency between these two points, which is definitely not normal in a linear (no harmonics), balanced Y system.

Finally, the voltage as measured across one of the load’s phases (between nodes 8 and 7 in the SPICE analysis) likewise shows strong triplen harmonic voltages of 50 volts each.

The figure below is a graphical summary of the aforementioned effects.

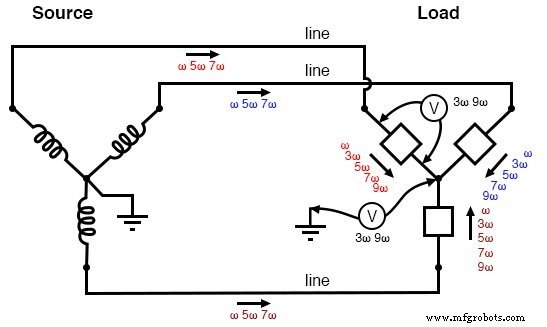
Three-wire “Y-Y” (no neutral) system:Triplen voltages appear between “Y” centers. Triplen voltages appear across load phases. Non-triplen currents appear in line conductors.

In summary, removal of the neutral conductor leads to a “hot” center-point on the load “Y”, and also to harmonic load phase voltages of equal magnitude, all comprised of triplen frequencies.

In the previous simulation where we had a 4-wire, Y-connected system, the undesirable effect from harmonics was excessive neutral current , but at least each phase of the load received voltage nearly free of harmonics.

Analysis of the Effects of Triplen Harmonics in a Delta-Wye(Y) Circuit

Since removing the neutral wire didn’t seem to work in eliminating the problems caused by harmonics, perhaps switching to a Δ configuration will. Let’s try a Δ source instead of a Y, keeping the load in its present Y configuration, and see what happens.

The measured parameters will be line current (voltage across R_line , nodes 0 and 8), load phase voltage (nodes 8 and 7), and source phase current (voltage across R_source , nodes 1 and 2). (Рисунок ниже)

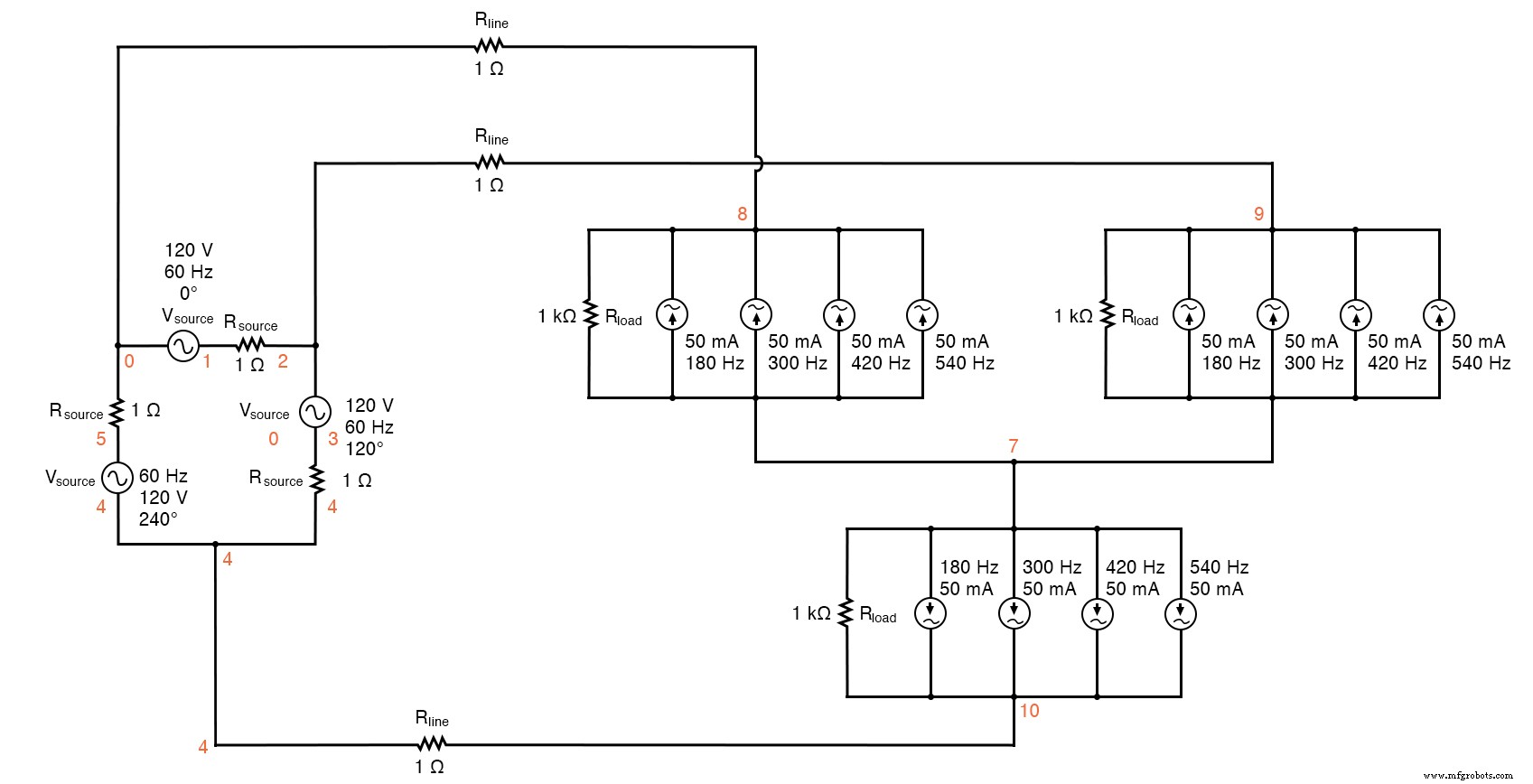
Delta-Y source/load with harmonics

Delta-Y source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 207.846 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 207.846 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 9.72222m 0) i5har1 8 7 sin(0 50m 300 9.72222m 0) i7har1 8 7 sin(0 50m 420 9.72222m 0) i9har1 8 7 sin(0 50m 540 9.72222m 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 15.2777m 0) i5har2 9 7 sin(0 50m 300 15.2777m 0) i7har2 9 7 sin(0 50m 420 15.2777m 0) i9har2 9 7 sin(0 50m 540 15.2777m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 4.16666m 0) i5har3 10 7 sin(0 50m 300 4.16666m 0) i7har3 10 7 sin(0 50m 420 4.16666m 0) i9har3 10 7 sin(0 50m 540 4.16666m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,8) v(8,7) v(1,2) .four 60 v(0,8) v(8,7) v(1,2) .конец 

Note:the following paragraph is for those curious readers who follow every detail of my SPICE netlists. If you just want to find out what happens in the circuit, skip this paragraph!

When simulating circuits having AC sources of differing frequency and differing phase, the only way to do it in SPICE is to set up the sources with a delay time or phase offset specified in seconds. Thus, the 0° source has these five specifying figures:“(0 207.846 60 0 0)”, which means 0 volts DC offset, 207.846 volts peak amplitude (120 times the square root of three, to ensure the load phase voltages remain at 120 volts each), 60 Hz, 0 time delay, and 0 damping factor.

The 120° phase-shifted source has these figures:“(0 207.846 60 5.55555m 0)”, all the same as the first except for the time delay factor of 5.55555 milliseconds, or 1/3 of the full period of 16.6667 milliseconds for a 60 Hz waveform.

The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.

This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.

If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.

This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).

One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.

The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.

Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:

Fourier analysis of line current:

 Fourier components of transient response v(0,8) dc component =-6.850E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 150.000 0.000 2 1.200E+02 2.491E-11 0.000000 159.723 9.722 3 1.800E+02 1.506E-06 0.000013 0.005 -149.996 4 2.400E+02 2.033E-11 0.000000 52.772 -97.228 5 3.000E+02 4.994E-02 0.416682 30.002 -119.998 6 3.600E+02 1.234E-11 0.000000 57.802 -92.198 7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995 total harmonic distortion =58.925038 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent 

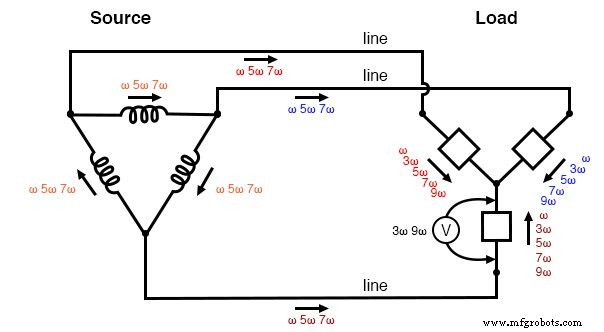
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.

Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.

The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.

It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.

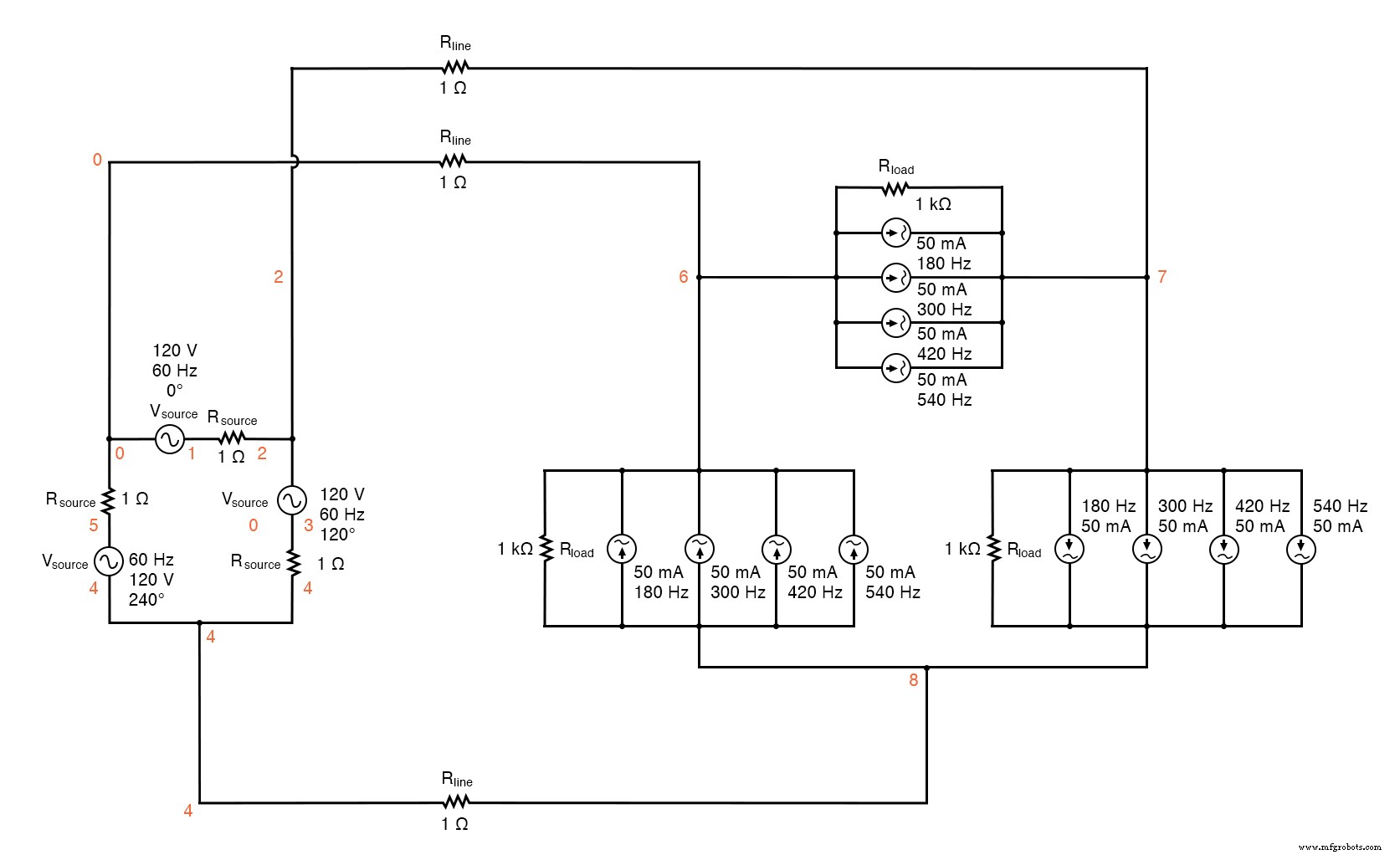
Delta-Delta source/load with harmonics.

Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .конец 

Fourier analysis of line current:

Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent 

As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.

But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.

Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.

What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.

These results may be graphically summarized as such in the figure below.

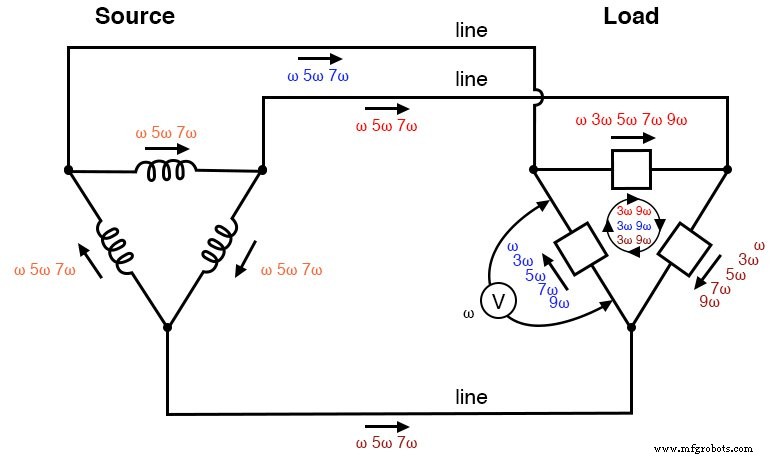
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.

This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.

ОБЗОР:

• Nonlinear components are those that draw a non-sinusoidal (non-sine-wave) current waveform when energized by a sinusoidal (sine-wave) voltage. Since any distortion of an originally pure sine-wave constitutes harmonic frequencies, we can say that nonlinear components generate harmonic currents.
• When the sine-wave distortion is symmetrical above and below the average centerline of the waveform, the only harmonics present will be odd-numbered , not even-numbered.
• The 3rd harmonic, and integer multiples of it (6th, 9th, 12th, 15th) are known as triplen harmonics. They are in phase with each other, despite the fact that their respective fundamental waveforms are 120° out of phase with each other.
• In a 4-wire Y-Y system, triplen harmonic currents add within the neutral conductor.
• Triplen harmonic currents in a Δ-connected set of components circulate within the loop formed by the Δ.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Mixed-Frequency Signals Worksheet