Сигналы прямоугольной волны

Было обнаружено, что любой Повторяющаяся несинусоидальная форма волны может быть приравнена к комбинации постоянного напряжения, синусоидальных и / или косинусоидальных волн (синусоидальных волн с фазовым сдвигом 90 градусов) с различными амплитудами и частотами.

Это верно независимо от того, насколько странной или запутанной может быть рассматриваемая форма волны. Если он регулярно повторяется с течением времени, его можно свести к этой серии синусоидальных волн.

В частности, было обнаружено, что прямоугольные волны математически эквивалентны сумме синусоидальной волны на той же частоте плюс бесконечная серия синусоидальных волн с нечетно-кратной частотой с уменьшающейся амплитудой:

Эта правда о формах волны на первый взгляд может показаться слишком странной, чтобы в нее поверить. Однако, если прямоугольная волна на самом деле представляет собой бесконечную серию сложенных вместе синусоидальных гармоник, очевидно, что мы сможем доказать это, сложив вместе несколько гармоник синусоидальной волны, чтобы получить близкое приближение к прямоугольной волне.

Это рассуждение не только убедительно, но и легко продемонстрировано с помощью SPICE.

Схема, которую мы будем моделировать, представляет собой не что иное, как несколько последовательно соединенных друг с другом источников синусоидального переменного напряжения соответствующей амплитуды и частоты. Мы будем использовать SPICE, чтобы построить кривые напряжения при последовательном добавлении источников напряжения, например:

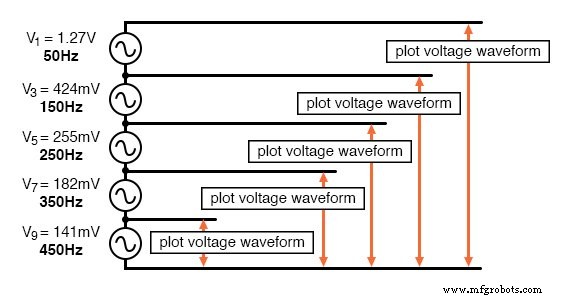
Прямоугольная волна аппроксимируется суммой гармоник.

В этом конкретном моделировании SPICE я суммировал последовательно последовательно включенные источники напряжения 1-й, 3-й, 5-й, 7-й и 9-й гармоник, всего пять источников переменного напряжения. Основная частота составляет 50 Гц, и каждая гармоника, конечно, кратна этой частоте.

Цифры амплитуды (напряжения) не являются случайными числами; скорее, они были получены с помощью уравнений, показанных в частотном ряду (дробь 4 / π, умноженная на 1, 1/3, 1/5, 1/7 и т. д. для каждой возрастающей нечетной гармоники).

 создание квадратной волны v1 1 0 sin (0 1,27324 50 0 0) 1-я гармоника (50 Гц) v3 2 1 sin (0 424.413m 150 0 0) 3-я гармоника v5 3 2 sin (0 254.648m 250 0 0) 5-я гармоника v7 4 3 sin (0 181.891m 350 0 0) 7-я гармоника v9 5 4 sin (0 141.471m 450 0 0) 9-я гармоника r1 5 0 10к .tran 1м 20м .plot tran v (1,0) График 1-й гармоники .plot tran v (2,0) График 1-й + 3-й гармоник .plot tran v (3,0) График 1-й + 3-й + 5-й гармоник .plot tran v (4,0) График 1-й + 3-й + 5-й + 7-й гармоник . участок tran v (5,0) Участок 1-й +. . . + 9-я гармоника .конец 

Я расскажу об анализе шаг за шагом, объясняя, на что мы смотрим. На этом первом графике мы видим синусоидальную волну основной частоты 50 Гц. Это не что иное, как чистая синусоида без дополнительных гармоник. Это форма волны, генерируемая идеальным источником питания переменного тока:

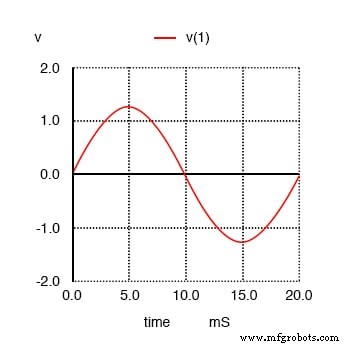
Чистая синусоида 50 Гц .

Затем мы увидим, что происходит, когда этот чистый и простой сигнал объединяется с третьей гармоникой (трижды по 50 Гц или 150 Гц). Внезапно он больше не выглядит как чистая синусоида:

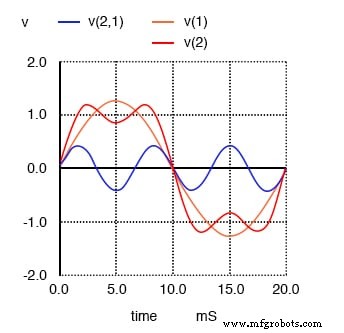
Сумма 1-й (50 Гц) и 3-й (150 Гц) гармоник приблизительно равна прямоугольной волне 50 Гц.

Время нарастания и спада между положительными и отрицательными циклами теперь намного круче, а гребни волны ближе к тому, чтобы стать плоскими, как прямоугольная волна. Посмотрите, что происходит, когда мы добавляем следующую нечетную частоту гармоники:

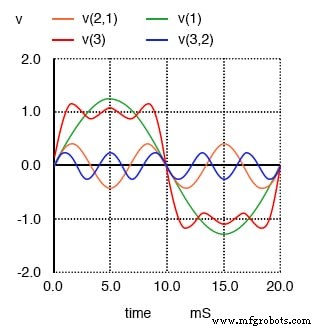
Сумма 1-й, 3-й и 5-й гармоник приблизительно равна прямоугольной волне.

Наиболее заметным изменением здесь является то, что гребни волны стали еще более плоскими. На каждом конце волны есть несколько провалов и гребней, но эти провалы и гребни меньше по амплитуде, чем были раньше. Посмотрите еще раз, как мы добавляем в микс следующую форму волны нечетной гармоники:

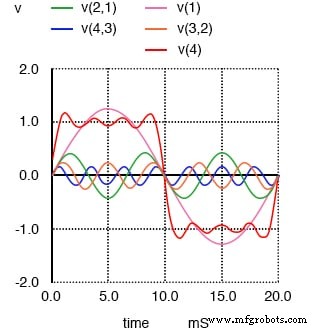
Сумма 1-й, 3-й, 5-й и 7-й гармоник приблизительно равна прямоугольной волне.

Здесь мы видим, что волна становится более плоской на каждом пике. Наконец, добавив 9-ю гармонику, пятый источник синусоидального напряжения в нашу схему, мы получим следующий результат:

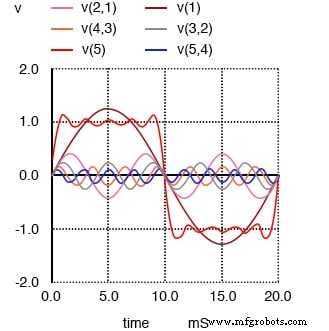
Сумма 1-й, 3-й, 5-й, 7-й и 9-й гармоник приблизительно равна прямоугольной волне.

Конечным результатом сложения первых пяти нечетных гармонических сигналов вместе (конечно, с правильными амплитудами) является близкое приближение к прямоугольной волне. Смысл этого в том, чтобы проиллюстрировать, как мы можем построить прямоугольную волну из множества синусоидальных волн на разных частотах, чтобы доказать, что чистая прямоугольная волна на самом деле эквивалентна серии синусоидальных волн.

Когда прямоугольное переменное напряжение подается в цепь с реактивными компонентами (конденсаторами и катушками индуктивности), эти компоненты реагируют так, как если бы они подвергались воздействию нескольких синусоидальных напряжений с разными частотами, что на самом деле так и есть.

Тот факт, что повторяющиеся несинусоидальные волны эквивалентны определенной серии аддитивного постоянного напряжения, синусоидальных и / или косинусоидальных волн, является следствием того, как работают волны:фундаментальным свойством всех связанных с волнами явлений, электрических или иных.

Математический процесс сведения несинусоидальной волны к этим составляющим частотам называется анализом Фурье . , подробности которого выходят за рамки этого текста. Тем не менее, были созданы компьютерные алгоритмы для выполнения этого анализа на высоких скоростях на реальных сигналах, и их применение для оценки качества электроэнергии переменного тока и анализа сигналов широко распространено.

SPICE может выполнять выборку формы волны и преобразовывать ее в составляющие гармоники синусоидальной волны с помощью преобразования Фурье . алгоритм, выводящий частотный анализ в виде таблицы чисел. Давайте попробуем это на прямоугольной волне, которая, как мы уже знаем, состоит из нечетно-гармонических синусоид:

 список соединений для анализа прямоугольных волн v1 1 0 импульс (-1 1 0, 1 м. 1 м 10 м 20 м) r1 1 0 10к .tran 1м 40м .plot tran v (1,0) . четыре 50 в (1,0) .конец 

пульс опция в строке списка соединений, описывающая источник напряжения v1 дает команду SPICE имитировать прямоугольную «импульсную» форму волны, в данном случае симметричную (равное время для каждого полупериода) и имеющую пиковую амплитуду 1 вольт. Сначала построим прямоугольную волну для анализа:

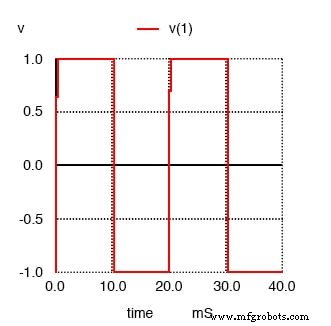
Прямоугольная волна для анализа Фурье SPICE

Затем мы напечатаем анализ Фурье, сгенерированный SPICE для этой прямоугольной волны:

 фурье-компоненты переходной характеристики v (1) компонент постоянного тока =-2,439E-02 гармоническая частота, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 5.000E + 01 1.274E + 00 1.000000 -2.195 0.000 2 1.000E + 02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E + 02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E + 02 4.936E-02 0,038757 -98,780 -96,585 5 2.500E + 02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E + 02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E + 02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E + 02 5.116E-02 0,040175 -107,561 -105,366 9 4.500E + 02 1.443E-01 0.113316 -19.756 -17.561 общее гармоническое искажение =43,805747 процентов 

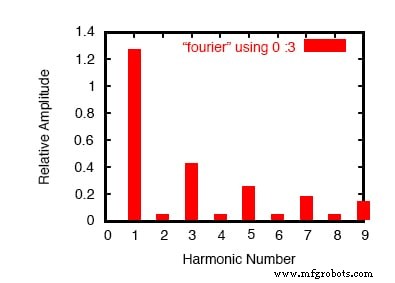
График результатов анализа Фурье.

Здесь (рисунок выше) SPICE разбил форму волны на спектр синусоидальных частот вплоть до девятой гармоники, плюс небольшое напряжение постоянного тока, помеченное DC component .

Мне пришлось сообщить SPICE основную частоту (для прямоугольной волны с периодом 20 миллисекунд эта частота составляет 50 Гц), поэтому он знал, как классифицировать гармоники. Обратите внимание, насколько малы цифры для всех четных гармоник (2-я, 4-я, 6-я, 8-я) и как уменьшаются амплитуды нечетных гармоник (1-я наибольшая, 9-я наименьшая).

Тот же самый метод «преобразования Фурье» часто используется в компьютеризированных силовых приборах, где производится выборка формы (сигналов) переменного тока и определение их гармонического содержания. Распространенным компьютерным алгоритмом (последовательностью шагов программы для выполнения задачи) для этого является быстрое преобразование Фурье . или БПФ функция.

Вам не нужно беспокоиться о том, как именно работают эти компьютерные процедуры, но нужно знать об их существовании и применении.

Тот же математический метод, который используется в SPICE для анализа гармонического содержания волн, может быть применен к техническому анализу музыки:разбиение любого конкретного звука на составляющие его частоты синусоидальной волны.

Фактически, вы, возможно, уже видели устройство, предназначенное именно для этого, не осознавая, что это было! графический эквалайзер представляет собой высококачественное стереооборудование, которое контролирует (а иногда и отображает) характер гармонического содержания музыки.

Оснащенный несколькими ручками или ползунками, эквалайзер может выборочно ослаблять (уменьшать) амплитуду определенных частот, присутствующих в музыке, для «настройки» звука в интересах слушателя. Обычно рядом с каждым рычагом управления отображается «гистограмма», отображающая амплитуду каждой конкретной частоты.

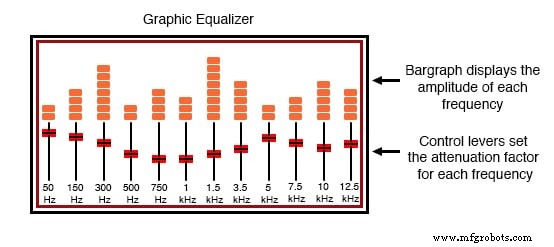
Графический эквалайзер Hi-Fi.

Устройство, предназначенное исключительно для отображения, а не управления, амплитуд каждого частотного диапазона для сигнала со смешанными частотами, обычно называется анализатором спектра . .

Конструкция анализаторов спектра может быть такой же простой, как набор схем «фильтров» (подробности см. В следующей главе), предназначенных для разделения разных частот друг от друга, или такой сложной, как специальный цифровой компьютер, на котором выполняется алгоритм БПФ для математически разделить сигнал на гармонические составляющие.

Анализаторы спектра часто предназначены для анализа чрезвычайно высокочастотных сигналов, таких как сигналы, создаваемые радиопередатчиками и компьютерным сетевым оборудованием. В таком виде они часто выглядят как осциллограф:

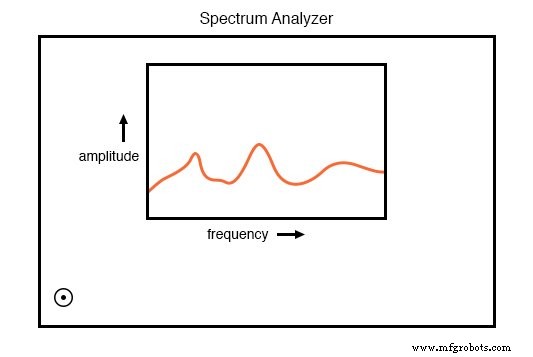
Анализатор спектра показывает амплитуду как функцию частоты.

Подобно осциллографу, анализатор спектра использует ЭЛТ (или компьютерный дисплей, имитирующий ЭЛТ) для отображения графика сигнала.

В отличие от осциллографа, на этом графике амплитуда зависит от частоты . а не амплитуда за время . По сути, частотный анализатор дает оператору график сигнала Боде:то, что инженер может назвать частотной областью вместо временной области анализ.

Термин «область» является математическим:сложное слово для описания горизонтальной оси графика. Таким образом, график осциллографа амплитуды (по вертикали) во времени (по горизонтали) представляет собой анализ «во временной области», тогда как график анализатора спектра амплитуды (по вертикали) по частоте (по горизонтали) представляет собой анализ «в частотной области».

Когда мы используем SPICE для построения графика амплитуды сигнала (амплитуды напряжения или тока) в диапазоне частот, мы выполняем частотную область анализ.

Обратите внимание на то, что анализ Фурье из последнего моделирования SPICE не «идеален». В идеале амплитуды всех четных гармоник должны быть абсолютно нулевыми, как и составляющая постоянного тока. Опять же, это не столько причуда SPICE, сколько свойство сигналов в целом.

Форма волны бесконечной продолжительности (бесконечное количество циклов) может быть проанализирована с абсолютной точностью, но чем меньше циклов доступно компьютеру для анализа, тем менее точен анализ. Только когда у нас есть уравнение, полностью описывающее форму волны, анализ Фурье может свести ее к определенной серии синусоидальных сигналов.

Чем меньше циклов волна повторяет, тем менее определена ее частота. Если довести эту концепцию до логического предела, короткий импульс - форма волны, которая даже не завершает цикл - на самом деле не имеет частоты , а скорее действует как бесконечный диапазон частот. Этот принцип является общим для всех волновые явления, а не только переменные напряжения и токи.

Достаточно сказать, что количество циклов и достоверность частотной составляющей сигнала напрямую связаны.

Мы могли бы улучшить точность нашего анализа, позволив волне колебаться в течение многих циклов, и в результате был бы спектральный анализ, более соответствующий идеалу. В следующем анализе для краткости я опустил график формы волны - это просто действительно длинная прямоугольная волна:

 прямоугольная волна v1 1 0 импульс (-1 1 0, 1 м. 1 м 10 м 20 м) r1 1 0 10к .option limpts =1001 .tran 1м 1 .plot tran v (1,0) . четыре 50 в (1,0) .конец компоненты Фурье переходной характеристики v (1) компонент постоянного тока =9.999E-03 гармоническая частота, нормализованная по Фурье, фаза, нормализованная нет (hz) компонент компонент (град) фаза (град) 1 5.000E + 01 1.273E + 00 1.000000 -1.800 0.000 2 1.000E + 02 1.999E-02 0.015704 86.382 88.182 3 1.500E + 02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E + 02 1.997E-02 0,015688 82,764 84,564 5 2.500E + 02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E + 02 1.994E-02 0,015663 79,146 80,946 7 3.500E + 02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E + 02 1.989E-02 0,015627 75,529 77,329 9 4.500E + 02 1.396E-01 0.109662 -16.199 -14.399 

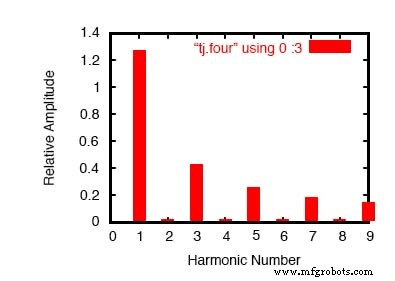
Улучшенный анализ Фурье.

Обратите внимание, как этот анализ (рисунок выше) показывает меньшее напряжение составляющей постоянного тока и меньшие амплитуды для каждой синусоидальной волны с четной гармонической частотой, все потому, что мы позволяем компьютеру измерять больше периодов волны. Опять же, неточность первого анализа - это не столько недостаток SPICE, сколько фундаментальное свойство волн и анализа сигналов.

ОБЗОР:

• Прямоугольные волны эквивалентны синусоиде на той же (основной) частоте, добавленной к бесконечному ряду нечетно-кратных синусоидальных гармоник с уменьшающимися амплитудами.
• Существуют компьютерные алгоритмы, которые могут выбирать формы волн и определять составляющие их синусоидальные компоненты. Преобразование Фурье алгоритм (в частности, быстрое преобразование Фурье , или БПФ ) обычно используется в программах моделирования компьютерных схем, таких как SPICE, и в электронном измерительном оборудовании для определения качества электроэнергии.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица сигналов прямоугольной волны