Текущие схемы делителя и формула текущего делителя

Параллельную цепь часто называют делителем тока . за его способность пропорционально или делить общий ток на дробные части.

Чтобы понять, что это означает, давайте сначала проанализируем простую параллельную цепь, определив токи ответвления через отдельные резисторы

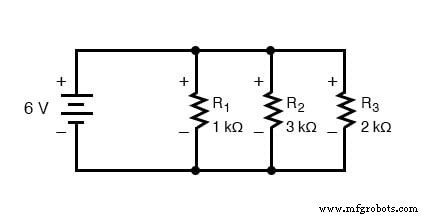
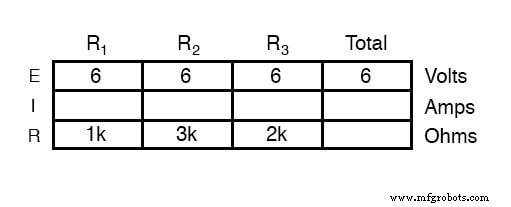
Зная, что напряжения на всех компонентах в параллельной цепи одинаковы, мы можем заполнить нашу таблицу напряжение / ток / сопротивление, указав 6 вольт в верхней строке:

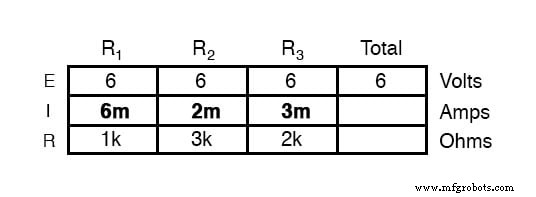
Используя закон Ома (I =E / R), мы можем рассчитать ток каждой ветви:

Зная, что токи ответвлений складываются в параллельных цепях, чтобы равняться общему току, мы можем получить общий ток, суммируя 6 мА, 2 мА и 3 мА:

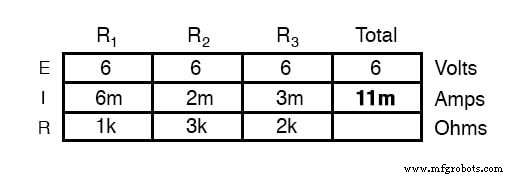
Последний шаг, конечно же, - это подсчитать полное сопротивление. Это можно сделать с помощью закона Ома (R =E / I) в столбце «общее» или с помощью формулы параллельного сопротивления для отдельных сопротивлений. В любом случае мы получим один и тот же ответ:

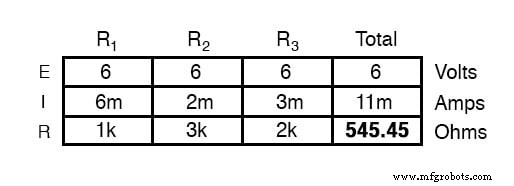
Еще раз, должно быть очевидно, что ток через каждый резистор связан с его сопротивлением, учитывая, что напряжение на всех резисторах одинаково. Здесь соотношение не прямо пропорционально, а наоборот. Например, ток через R ₁ вдвое больше, чем ток через R ₃ , который имеет удвоенное сопротивление R ₁ .

Если бы мы изменили напряжение питания этой схемы, мы обнаружили, что (сюрприз!) Эти пропорции не меняются:

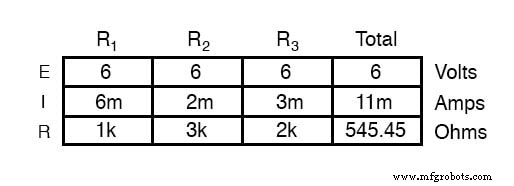
Расчет коэффициентов текущей ликвидности

Ток через R ₁ по-прежнему ровно вдвое больше, чем R ₃ , несмотря на то, что напряжение источника изменилось. Пропорциональность между разными токами ответвления строго зависит от сопротивления.

Делители напряжения напоминают также тот факт, что токи ответвления представляют собой фиксированные пропорции общего тока. Несмотря на четырехкратное увеличение напряжения питания, соотношение между током любой ветви и полным током остается неизменным:

Теперь мы можем сами убедиться в том, что мы отметили в начале этой страницы:параллельную цепь часто называют делителем тока . за его способность пропорционально или делить общий ток на дробные части.

Текущая формула делителя

Приложив немного алгебры, мы можем вывести формулу для определения тока параллельного резистора, учитывая не что иное, как общий ток, отдельное сопротивление и общее сопротивление:

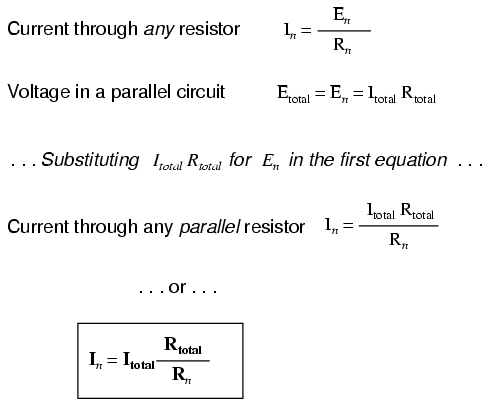
Отношение полного сопротивления к индивидуальному сопротивлению такое же, как отношение индивидуального (ответвления) тока к общему току. Это известно как формула текущего делителя . , и это сокращенный метод определения токов ответвления в параллельной цепи, когда известен полный ток.

Пример формулы текущего делителя

Используя исходную параллельную схему в качестве примера, мы можем повторно рассчитать токи ответвления по этой формуле, если мы начнем с знания общего тока и общего сопротивления:

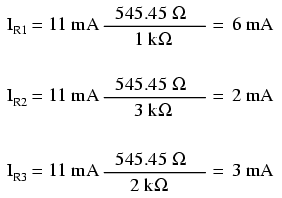
Если вы потратите время на сравнение двух формул делителя, вы увидите, что они очень похожи. Обратите внимание, однако, что коэффициент в формуле делителя напряжения равен R _n (индивидуальное сопротивление) деленное на R _Total , и как соотношение в текущей формуле делителя равно R _Total делится на R _n :

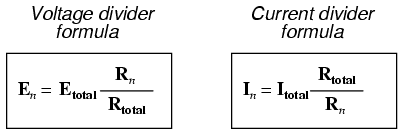
Формула делителя тока по сравнению с формулой делителя напряжения

Эти два уравнения довольно легко спутать, получив обратные соотношения сопротивлений. Один из способов помочь запомнить правильную форму - это помнить, что оба отношения в уравнениях делителя напряжения и тока должны быть меньше единицы. Ведь это разделитель уравнения, а не множитель уравнения! Если дробь перевернута, будет получено соотношение больше единицы, что неверно.

Зная, что полное сопротивление в последовательной цепи (делитель напряжения) всегда больше, чем любое из отдельных сопротивлений, мы знаем, что дробь для этой формулы должна быть R _n более R _Итого . И наоборот, зная, что полное сопротивление в параллельной цепи (делитель тока) всегда меньше любого из отдельных сопротивлений, мы знаем, что дробь для этой формулы должна быть R _Total над R _n .

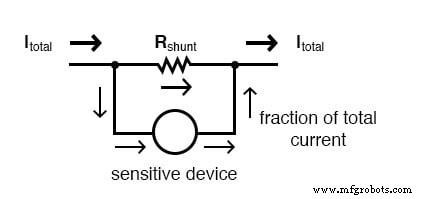
Пример применения схемы делителя тока:Схема электрического счетчика

Цепи делителя тока также находят применение в схемах электрических счетчиков, где желательно, чтобы часть измеренного тока проходила через чувствительное устройство обнаружения. Используя формулу делителя тока, подходящий шунтирующий резистор может быть подобран таким образом, чтобы пропорционально пропорции правильного количества тока для устройства в любом конкретном случае:

ОБЗОР:

• Параллельные цепи соотносят, или «делят», общий ток цепи между токами отдельных ветвей, причем пропорции строго зависят от сопротивлений:I _n =Я _Итого (R _Итого / R _n )

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист текущих схем делителя