Закон Кирхгофа о напряжении (KVL)

Что такое закон напряжения Кирхгофа (KVL)?

Принцип, известный как закон напряжения Кирхгофа (открытый в 1847 году немецким физиком Густавом Кирхгофом) можно сформулировать так:

«Алгебраическая сумма всех напряжений в контуре должна равняться нулю»

По алгебраической Я имею в виду учет знаков (полярностей), а также величин. По циклу , Я имею в виду любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи и, наконец, обратно в исходную точку.

Демонстрация закона напряжения Кирхгофа в последовательной цепи

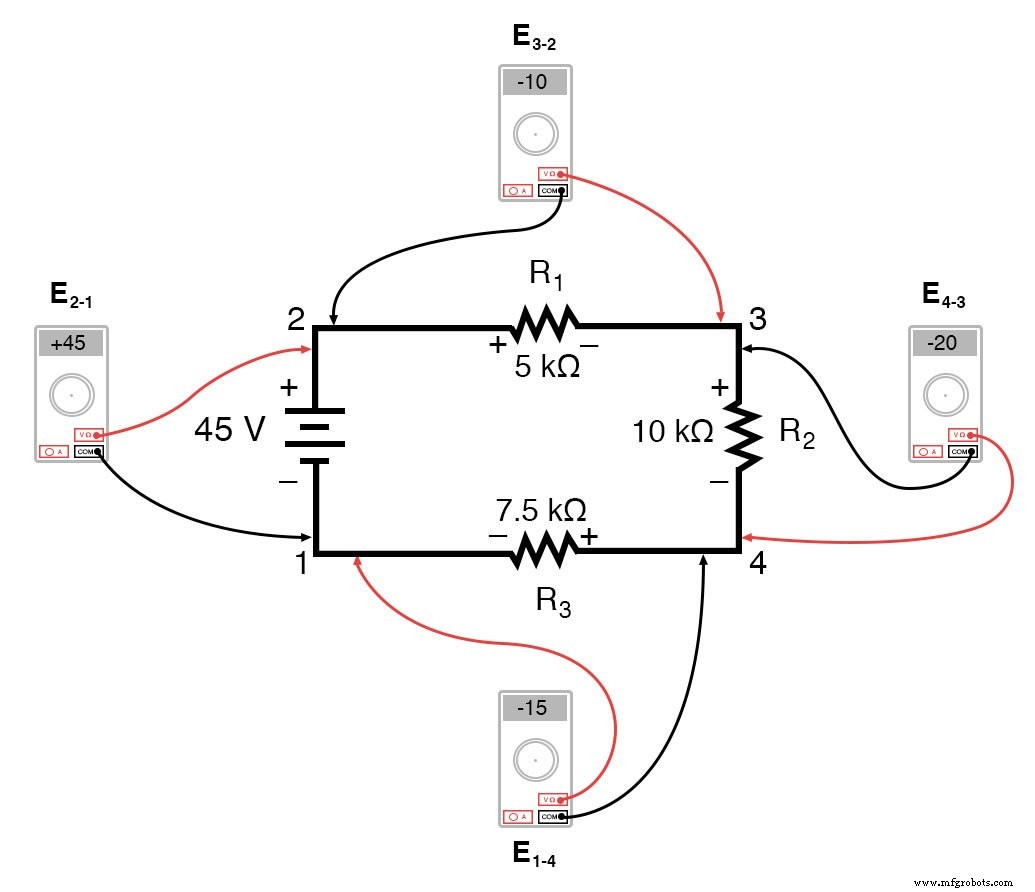
Давайте еще раз посмотрим на нашу примерную последовательную схему, на этот раз пронумеровав точки в цепи для опорного напряжения:

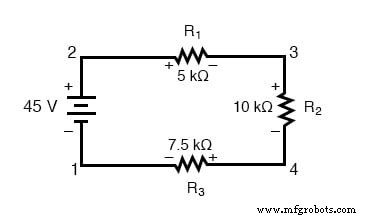
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, измеритель зарегистрировал бы +45 вольт. Обычно знак «+» не отображается, а скорее подразумевается для положительных показаний на дисплеях цифровых счетчиков. Однако для этого урока очень важна полярность показаний напряжения, поэтому я буду явно показывать положительные числа:

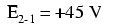
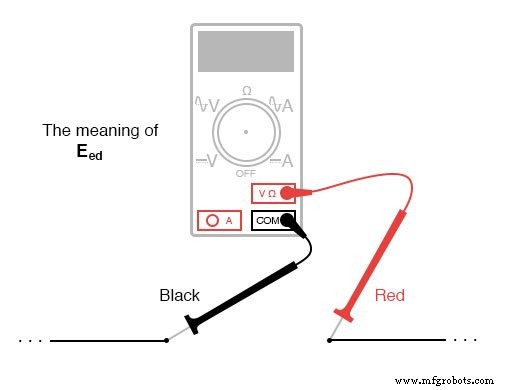
Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E _2-1 ”), Это означает напряжение в первой точке (2), измеренное относительно второй точки (1). Напряжение указано как «E _cd »Будет означать напряжение, показанное цифровым измерителем с красным измерительным проводом в точке« c »и черным измерительным проводом в точке« d »:напряжение в точке« c »относительно« d ».

Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего измерителя на точке впереди и черным измерительным проводом на точке сзади, мы бы получили следующие чтения:

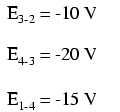
Мы уже должны быть знакомы с общим принципом для последовательных цепей, гласящим, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого. принцип:все измеренные напряжения в сумме равны нулю:

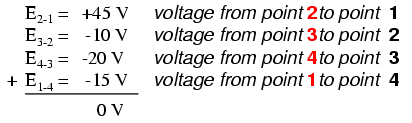
В приведенном выше примере петля образована следующими точками в указанном порядке:1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении идем, отслеживая петлю; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем подсчитать напряжения в контуре 3-2-1-4-3 той же цепи:

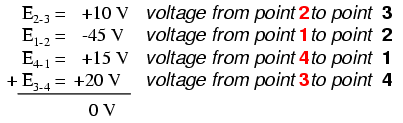
Это может иметь больше смысла, если мы перерисуем нашу схему последовательного соединения так, чтобы все компоненты были представлены в виде прямой линии:

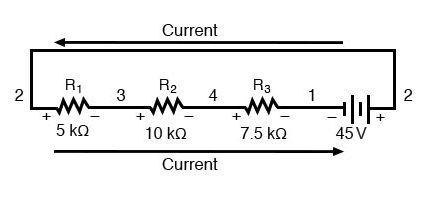
Это все та же последовательная схема, только с компонентами, расположенными в другой форме. Обратите внимание на полярность падения напряжения резистора по отношению к батарее:напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторе ориентированы в другую сторону:положительное слева и отрицательное справа. Это потому, что резисторы сопротивляются поток электрического заряда, проталкиваемый батареей. Другими словами, «толчок» со стороны резисторов против поток электрического заряда должен быть в направлении, противоположном источнику электродвижущей силы.

Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, черный провод слева и красный провод справа, как показано горизонтально:

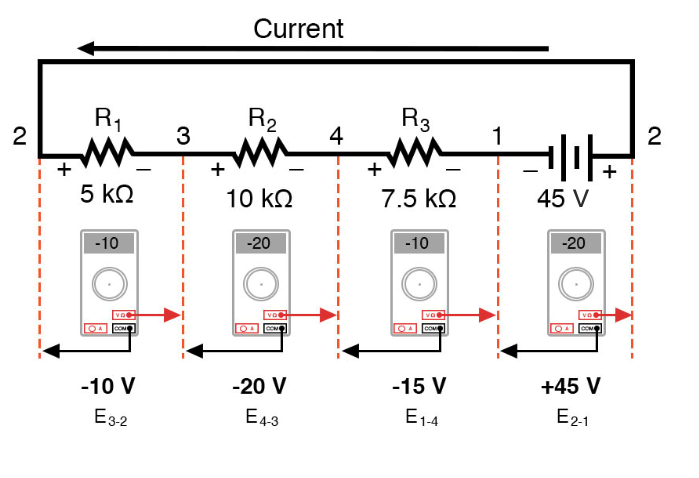
Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с одного R ₁ слева и продвигаясь по всей цепочке компонентов, мы увидим, как напряжения складываются алгебраически (до нуля):

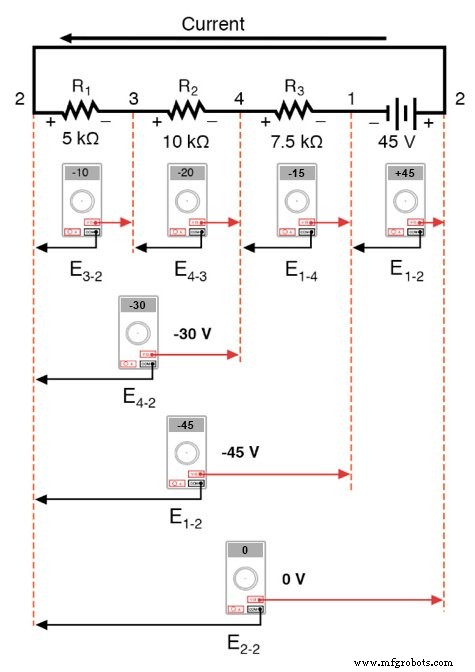
Тот факт, что последовательные напряжения суммируются, не должен быть секретом, но мы заметили, что полярность от этих напряжений имеет большое значение в сумме цифр. При считывании напряжения на R ₁ —R ₂ , и R ₁ —R ₂ —R ₃ (Я использую двойной дефис «-» для обозначения серии соединение между резисторами R ₁ , R ₂ , и R ₃ ), мы видим, как напряжения измеряют последовательно большие (хотя и отрицательные) величины, потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (положительный левый, отрицательный правый).

Сумма падений напряжения на R ₁ , R ₂ , и R ₃ равно 45 вольт, что соответствует выходу батареи, за исключением того, что полярность батареи противоположна падению напряжения на резисторе (отрицательное слева, положительное справа), поэтому мы получаем 0 вольт, измеренный на всей цепочке компонентов.

То, что мы должны получить ровно 0 вольт на всей струне, тоже не должно быть тайной. Глядя на схему, мы видим, что крайний левый угол строки (левая часть R ₁ :точка номер 2) напрямую подключается к крайнему правому краю строки (правая сторона батареи:точка номер 2), если это необходимо для завершения цепи.

Поскольку эти две точки соединены напрямую, они электрически общие . друг другу. Таким образом, напряжение между этими двумя электрически общими точками должно равняться нулю.

Демонстрация закона напряжения Кирхгофа в параллельной цепи

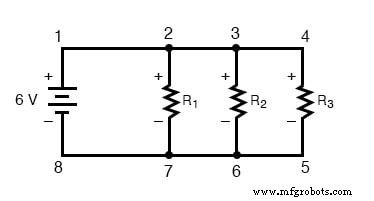
Закон Кирхгофа о напряжении (иногда обозначается как KVL для краткости) будет работать для любых схемотехническая конфигурация вообще, а не просто последовательная. Обратите внимание, как это работает для этой параллельной схемы:

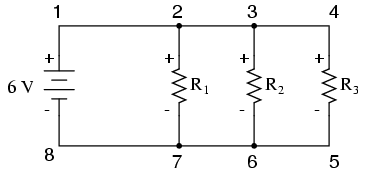
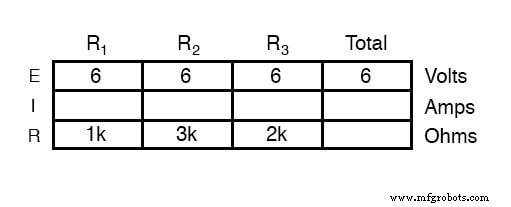
В параллельной схеме напряжение на каждом резисторе такое же, как и напряжение питания:6 вольт. Суммируя напряжения вокруг контура 2-3-4-5-6-7-2, мы получаем:

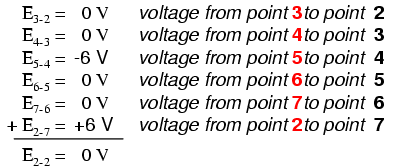
Обратите внимание, как я помечаю окончательное (суммарное) напряжение как E _2-2 . Поскольку мы начали нашу пошаговую последовательность в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E _2-2 ), который, конечно же, должен быть равен нулю.

Действительность закона Кирхгофа о напряжении независимо от топологии цепи

Тот факт, что эта схема является параллельной, а не последовательной, не имеет ничего общего с правомерностью закона Кирхгофа о напряжении. В этом отношении схема может быть «черным ящиком» - конфигурация ее компонентов полностью скрыта от нашего взгляда, с набором открытых клемм для измерения напряжения между ними - и KVL все равно останется верным:

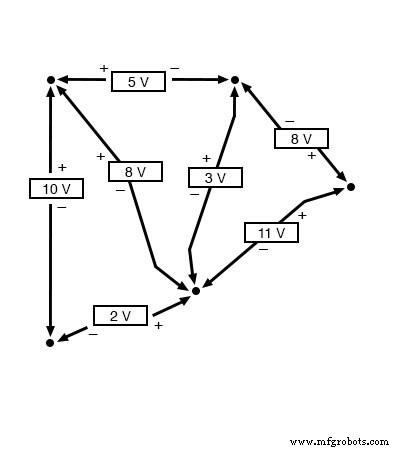
Попробуйте выполнить любой порядок шагов с любого терминала на приведенной выше диаграмме, вернувшись к исходному терминалу, и вы обнаружите, что алгебраическая сумма напряжений всегда равно нулю.

Более того, «контур», который мы отслеживаем для KVL, даже не обязательно должен быть реальным током в прямом смысле этого слова. Все, что нам нужно сделать, чтобы соответствовать KVL, - это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между следующей и последней точкой. Рассмотрим этот абсурдный пример, отслеживая «петлю» 2-3-6-3-2 в той же цепи параллельного резистора:

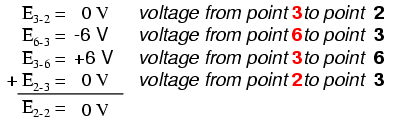
Использование закона Кирхгофа о напряжении в сложной цепи

KVL можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вокруг определенного «контура». В качестве примера возьмем следующую сложную схему (фактически две последовательные цепи, соединенные одним проводом внизу):

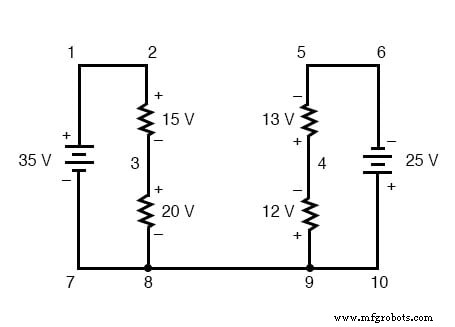
Чтобы упростить задачу, я опустил значения сопротивления и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют общий провод между собой (провод 7-8-9-10), что позволяет измерять напряжение между возможны две схемы. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение KVL с напряжением между этими точками как неизвестным:

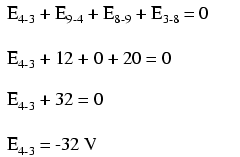
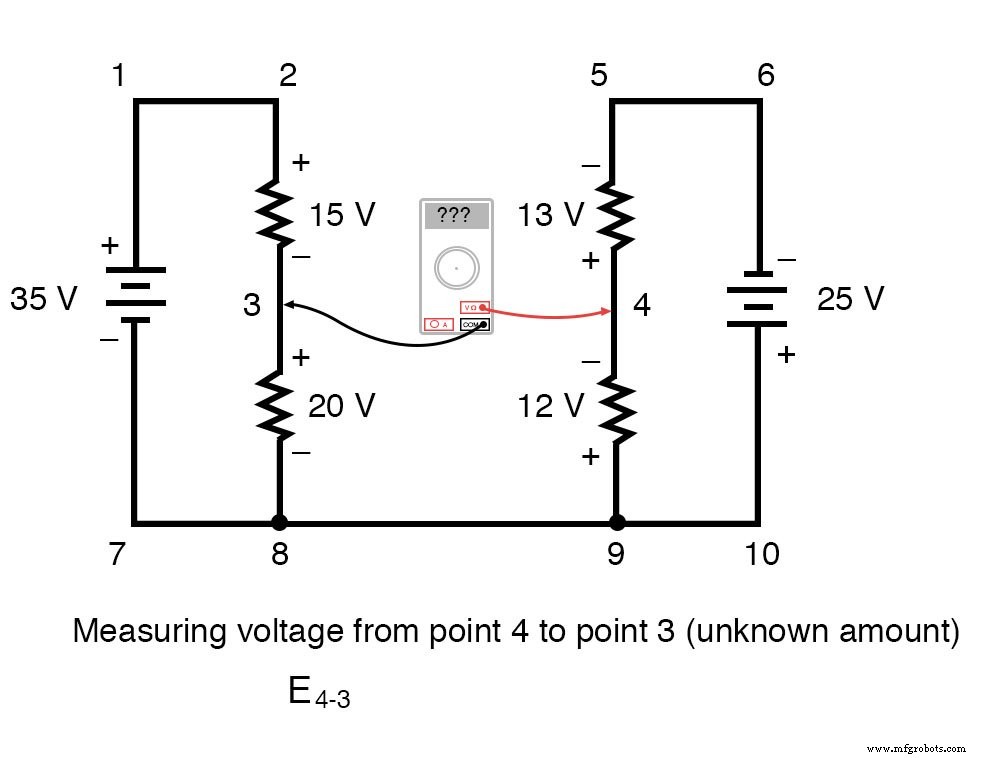
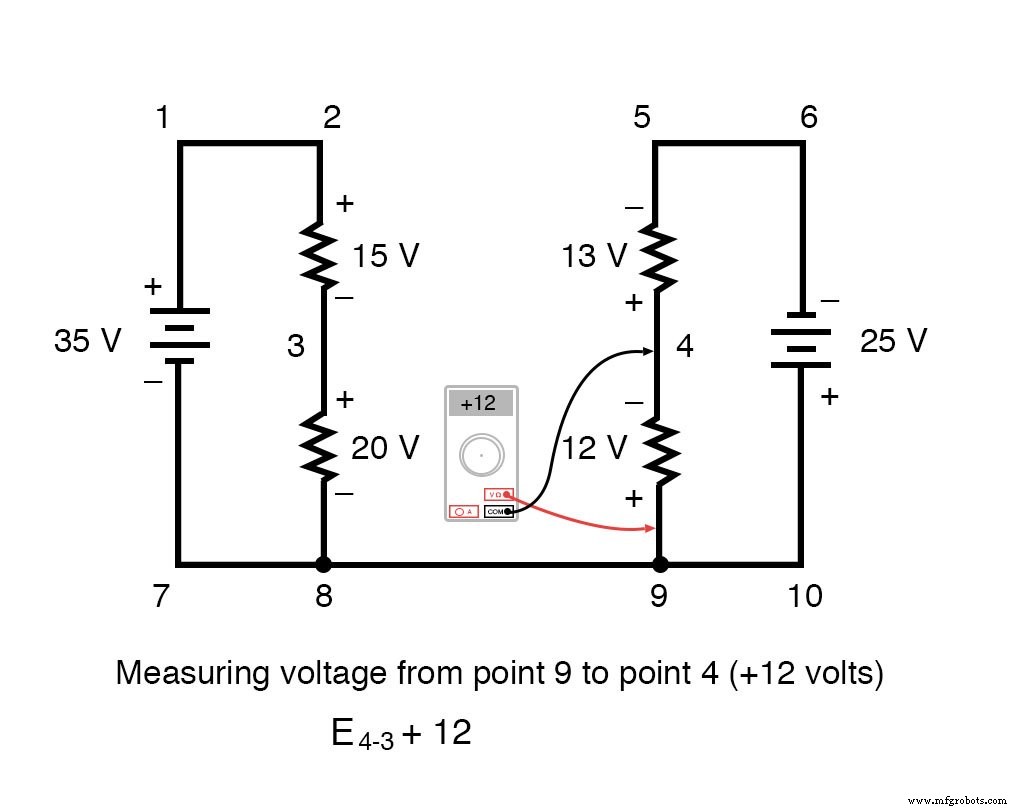
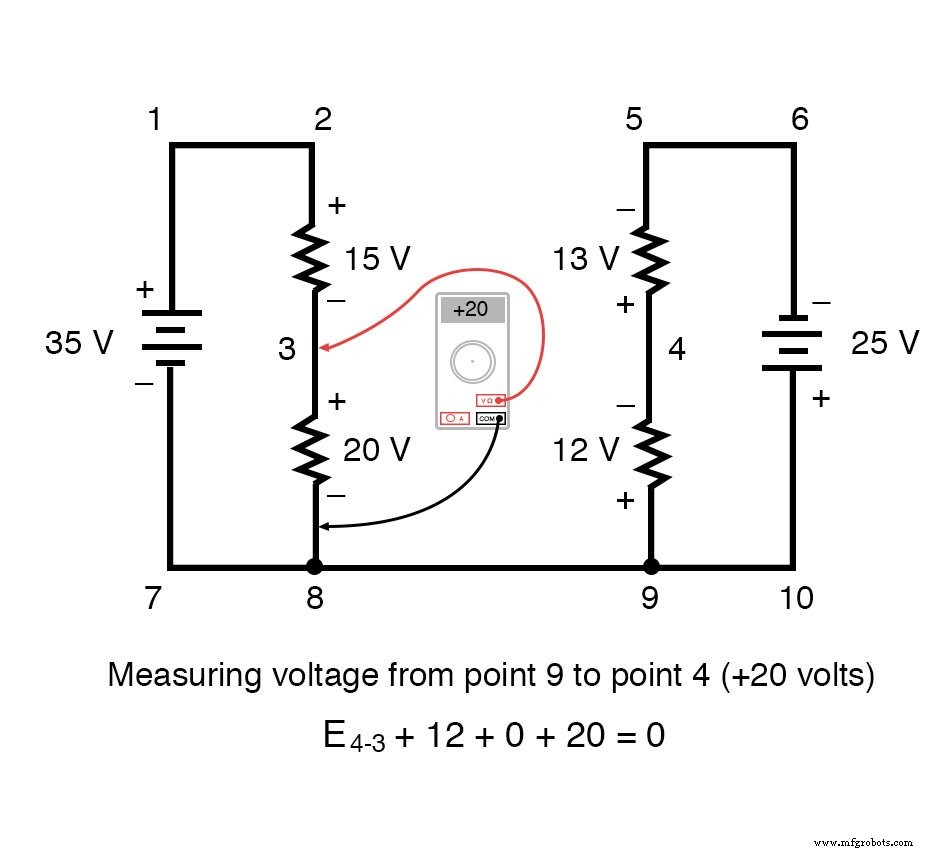
Обходя контур 3-4-9-8-3, мы записываем значения падения напряжения так, как их регистрировал бы цифровой вольтметр, выполняя измерения красным измерительным проводом на точке впереди и черным измерительным проводом на точке сзади по мере того, как мы продвигаемся вперед. петля. Следовательно, напряжение от точки 9 до точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» - в точке 4.

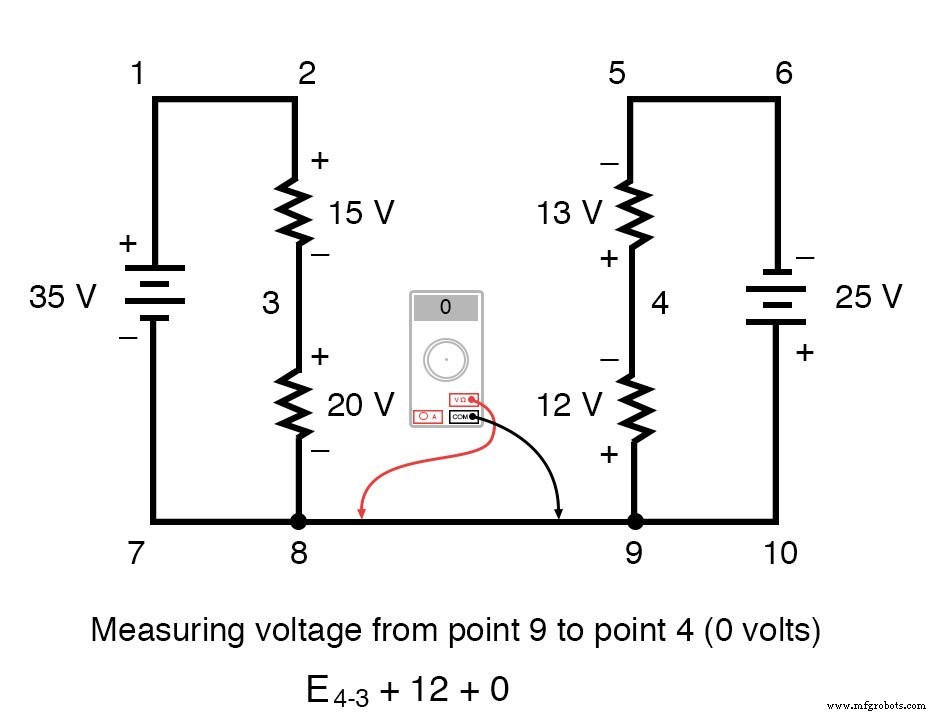
Напряжение от точки 3 до точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» - в точке 8. Напряжение от точки 8 до точки 9, конечно, равно нулю. , потому что эти две точки электрически общие.

Наш окончательный ответ для напряжения от точки 4 до точки 3 - это отрицательное (-) 32 вольта, говорящее нам, что точка 3 на самом деле положительна по отношению к точке 4, именно то, что цифровой вольтметр показал бы красным проводом в точке 4 и черный провод по пункту 3:

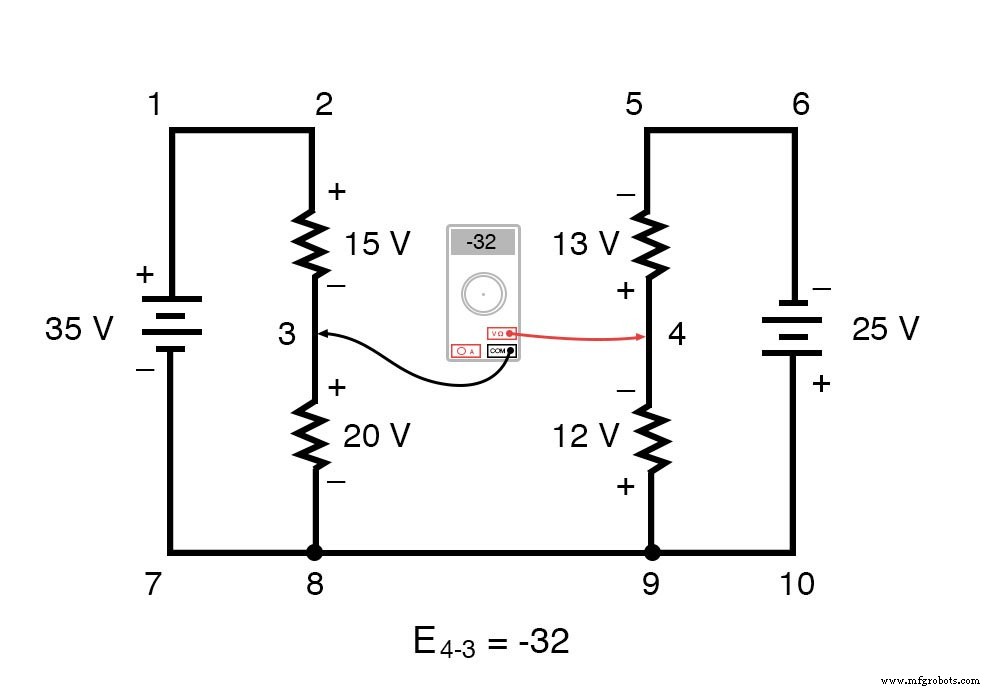
Другими словами, первоначальное размещение наших «выводов измерителя» в этой проблеме KVL было «обратным». Если бы мы сгенерировали наше уравнение KVL, начиная с E _3-4 вместо E _4-3 , пройдя по той же петле с противоположной ориентацией измерительных проводов, окончательным ответом будет E _3-4 =+32 вольт:

Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4:точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.

ОБЗОР:

• Закон Кирхгофа о напряжении (KVL): «Алгебраическая сумма всех напряжений в контуре должна равняться нулю»

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист законов Кирхгофа