Метод напряжения узла

Метод анализа узлового напряжения решает неизвестные напряжения в узлах схемы с помощью системы уравнений KCL. Этот анализ выглядит странным, потому что он предполагает замену источников напряжения эквивалентными источниками тока. Кроме того, значения резистора в омах заменяются эквивалентной проводимостью в сименсах, G =1 / R. Сименс (S) - это единица проводимости, заменившая единицу mho. В любом случае S =Ω-1. И S =mho (устарело).

Метод расчета напряжения узла

Начнем со схемы, имеющей обычные источники напряжения. Общий узел E ₀ выбран в качестве ориентира. Напряжения узлов E ₁ и E ₂ рассчитываются относительно этой точки.

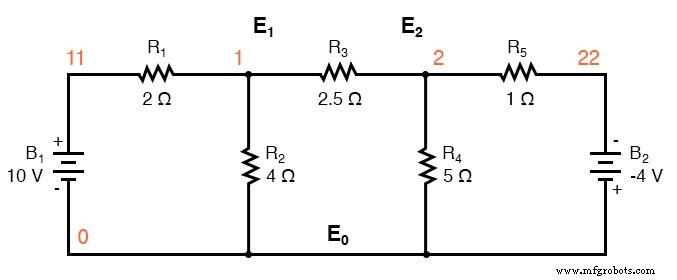
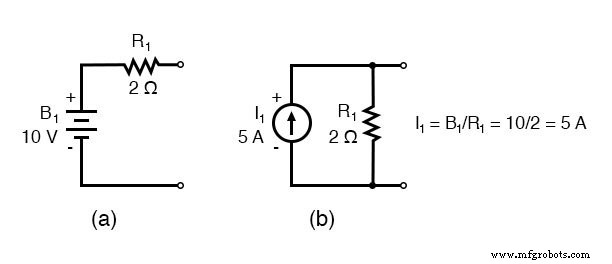
Замена источников напряжения и связанных последовательных резисторов эквивалентными источниками тока и параллельными резисторами дает модифицированную схему. Замените сопротивление в омах проводимость резистора в сименсах.

 I1 =E1 / R1 =10/2 =5 А I2 =E2 / R5 =4/1 =4 А G1 =1 / R1 =1/2 Ом =0,5 S G2 =1 / R2 =1/4 Ом =0,25 См G3 =1 / R3 =1 / 2,5 Ом =0,4 S G4 =1 / R4 =1/5 Ом =0,2 с G5 =1 / R5 =1/1 Ом =1,0 S 

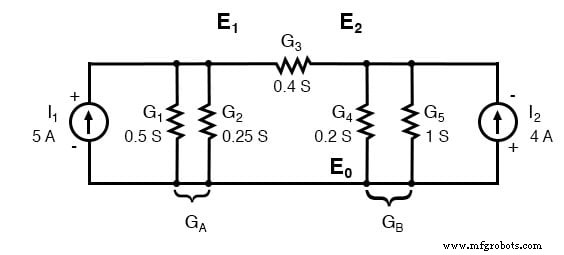
Параллельные проводимости (резисторы) могут быть объединены путем сложения проводимости. Но перерисовывать схему не будем. Схема готова к применению метода узлового напряжения.

 GA =G1 + G2 =0,5 S + 0,25 S =0,75 S GB =G4 + G5 =0,2 S + 1 S =1,2 S 

Получив общий метод узлового напряжения, мы запишем пару уравнений KCL в терминах неизвестных узловых напряжений V ₁ и V ₂ на этот раз. Мы делаем это, чтобы проиллюстрировать схему написания уравнений путем проверки.

 GAE1 + G3 (E1 - E2) =I1 (1) GBE2 - G3 (E1 - E2) =I2 (2) (GA + G3) E1 -G3E2 =I1 (1) -G3E1 + (GB + G3) E2 =I2 (2) 

Коэффициенты последней пары приведенных выше уравнений были изменены, чтобы показать закономерность. Сумма проводимостей, подключенных к первому узлу, является положительным коэффициентом первого напряжения в уравнении (1). Сумма проводимостей, подключенных ко второму узлу, является положительным коэффициентом второго напряжения в уравнении (2). Остальные коэффициенты отрицательны и представляют собой проводимость между узлами. Для обоих уравнений правая часть равна соответствующему источнику тока, подключенному к узлу. Этот шаблон позволяет нам быстро писать уравнения путем проверки. Это приводит к набору правил для метода анализа узлового напряжения.

Правила напряжения узла:

• Преобразуйте источники напряжения, включенные последовательно с резистором, в эквивалентный источник тока с параллельным резистором.
• Измените номиналы резисторов на проводимости.
• Выберите опорный узел (E ₀ )
• Назначить неизвестное напряжение (E ₁ ) (E ₂ ) ... (E _N ) к остальным узлам.
• Напишите уравнение KCL для каждого узла 1,2, ... N. Положительный коэффициент первого напряжения в первом уравнении представляет собой сумму проводимости, подключенной к узлу. Коэффициент для второго напряжения во втором уравнении представляет собой сумму проводимостей, подключенных к этому узлу. Повторите эти действия для коэффициента третьего напряжения, третьего уравнения и других уравнений. Эти коэффициенты попадают по диагонали.
• Все остальные коэффициенты для всех уравнений отрицательны и представляют собой проводимость между узлами. Первое уравнение, второй коэффициент - это проводимость от узла 1 к узлу 2, третий коэффициент - это проводимость от узла 1 к узлу 3. Заполните отрицательные коэффициенты для других уравнений.
• Правая часть уравнений - это источник тока, подключенный к соответствующим узлам.
• Решите систему уравнений для неизвестных узловых напряжений.

Пример метода определения напряжения узла

Пример: Составьте уравнения и решите для узловых напряжений, используя числовые значения на рисунке выше.

Решение:

 (0,5 + 0,25 + 0,4) E1 - (0,4) E2 =5 - (0,4) E1 + (0,4 + 0,2 + 1,0) E2 =-4 (1.15) E1 - (0.4) E2 =5 - (0,4) E1 + (1,6) E2 =-4 E1 =3,8095 E2 =-1,5476 

Решение двух уравнений может быть выполнено с помощью калькулятора или с октавой (не показано). Решение проверено в SPICE на основе оригинальной принципиальной схемы с источниками напряжения. Хотя схему с источниками тока можно было смоделировать.

 V1 11 0 постоянного тока 10 V2 22 0 DC -4 г1 11 1 2 г2 1 0 4 г3 1 2 2,5 г4 2 0 5 r5 2 22 1 .DC V1 10 10 1 V2 -4-4 1 .print DC В (1) В (2) .конец v (1) v (2) 3.809524e + 00 -1.547619e + 00 

Еще один пример. У этого есть три узла. Мы не приводим значения проводимости на принципиальной схеме. Однако G ₁ =1 / R ₁ и т. д.

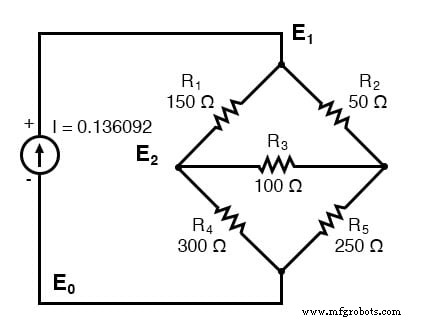
Есть три узла, для которых нужно написать уравнения путем проверки. Обратите внимание, что коэффициенты для уравнения (1) E ₁ положительны. , уравнение (2) E ₂ , и уравнение (3) E ₃ . Это суммы всех проводимостей, подключенных к узлам. Все остальные коэффициенты отрицательны, что указывает на проводимость между узлами. Правая часть уравнений - это связанный источник тока, 0,136092 А для единственного источника тока в узле 1. Остальные уравнения в правой части равны нулю из-за отсутствия источников тока. Нам лень рассчитывать проводимости резисторов на схеме. Таким образом, G в нижнем индексе - это коэффициенты.

 (G1 + G2) E1 -G1E2 -G2E3 =0,136092 -G1E1 + (G1 + G3 + G4) E2 -G3E3 =0 -G2E1 -G3E2 + (G2 + G3 + G5) E3 =0 

Мы настолько ленивы, что вводим взаимные сопротивления и суммы взаимных сопротивлений в матрицу октавы «А», позволяя октаве вычислить матрицу проводимости после «А =». Первоначальная строка входа была такой длинной, что ее разбили на три ряда. Это отличается от предыдущих примеров. Введенная матрица «А» обведена начальными и конечными квадратными скобками. Элементы столбца разделяются пробелами. Строки разделяются «новой строкой». Запятые и точки с запятой в качестве разделителей не нужны. Тем не менее, вектор тока в точке «b» разделяется точкой с запятой, чтобы получить вектор-столбец токов.

 октава:12> A =[1/150 + 1/50 -1/150 -1/50> -1/150 1/150 + 1/100 + 1/300 -1/100> -1/50 -1/100 1/50 + 1/100 + 1/250] А =0,0266667 -0,0066667 -0,0200000 -0,0066667 0,0200000 -0,0100000 -0,0200000 -0,0100000 0,0340000 октава:13> b =[0,136092; 0; 0] b =0,13609 0,00000 0,00000 октава:14> x =A \ b х =24,000 17,655 19,310 

Обратите внимание, что диагональные коэффициенты матрицы «A» положительны, а все остальные коэффициенты отрицательны.

Решение в виде вектора напряжения находится в точке «x». E ₁ =24,000 В, E ₂ =17,655 В, E ₃ =19,310 В. Эти три напряжения сравниваются с предыдущими значениями тока сетки и решениями SPICE для проблемы несимметричного моста. Это не совпадение, поскольку источник тока 0,13609 А был специально выбран для получения 24 В, используемого в качестве источника напряжения в этой задаче.

Резюме

• Учитывая сеть проводимости и источников тока, метод анализа цепей с помощью метода узлового напряжения решает неизвестные узловые напряжения из уравнений KCL.
• Подробные сведения о написании уравнений путем проверки см. в приведенных выше правилах.
• Единица проводимости G - это сименс S. Проводимость обратно пропорциональна сопротивлению:G =1 / R

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Таблица точных диодных схем
• Рабочий лист законов Кирхгофа