Конечные автоматы

До сих пор каждая представленная схема была комбинаторной схема. Это означает, что его выход зависит только от его текущих входов. Предыдущие входы для этого типа цепей не влияют на выход.

Однако есть много приложений, в которых наши схемы должны иметь «память»; запоминать предыдущие входы и рассчитывать свои выходы в соответствии с ними. Схема, выход которой зависит не только от текущего ввода, но и от истории ввода, называется последовательной схемой . .

В этом разделе мы узнаем, как спроектировать и построить такие последовательные схемы. Чтобы увидеть, как работает эта процедура, воспользуемся примером, на котором будем изучать нашу тему.

Итак, предположим, что у нас есть цифровая викторина, которая работает на часах и считывает данные, введенные вручную с помощью кнопки. Однако мы хотим, чтобы коммутатор передавал в схему только один HIGH-импульс. Если мы подключим кнопку непосредственно к игровой цепи, она будет передавать ВЫСОКОЕ значение в течение минимального количества тактовых циклов, которое может достичь наш палец. На обычной тактовой частоте наш палец никогда не может быть достаточно быстрым.

Процедура проектирования включает определенные шаги, которые необходимо выполнить, чтобы выполнить работу:

Шаг 1

Первым шагом процедуры проектирования является определение простыми, но понятными словами, что мы хотим, чтобы наша схема выполняла:

«Наша миссия состоит в том, чтобы разработать вторичную схему, которая будет передавать ВЫСОКИЙ импульс длительностью только один цикл при нажатии кнопки ручного управления и не будет передавать другой импульс, пока кнопка не будет нажата и снова нажата».

Шаг 2

Следующим шагом является создание диаграммы состояний.

Это диаграмма, составленная из кругов и стрелок и визуально описывающая работу нашей схемы. С математической точки зрения эта диаграмма, описывающая работу нашей последовательной схемы, является конечным автоматом. Обратите внимание, что это конечный автомат Мура.

Его выход является функцией только его текущего состояния, а не его входом. Это контрастирует с конечным автоматом Мили, где ввод влияет на вывод. В этом руководстве будет рассматриваться только конечный автомат Мура.

Диаграмма состояний нашей схемы следующая:(рисунок ниже)

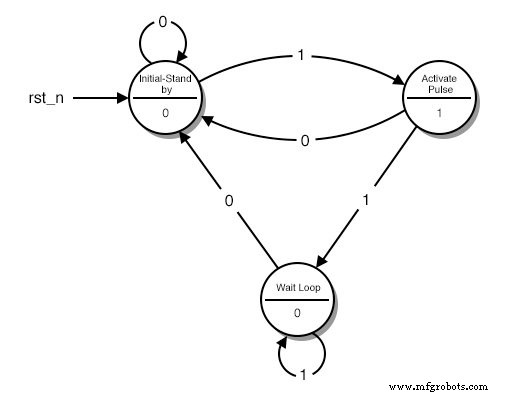
Диаграмма состояний

Каждый кружок представляет собой «состояние», четко определенное состояние, в котором находится наша машина. В верхней половине круга мы описываем это состояние. Описание помогает нам вспомнить, что наша схема должна делать в этих условиях.

• Первый кружок - состояние «ожидания». Здесь начинается наша схема и ждет следующего нажатия кнопки.
• Второй кружок - это условие, при котором кнопка была только что нажата, и наша схема должна передать ВЫСОКИЙ импульс.
• Третий кружок - это состояние, при котором наша схема ожидает отпускания кнопки, прежде чем вернуться в состояние «ожидания».

В нижней части круга - вывод нашей схемы. Если мы хотим, чтобы наша схема передавала HIGH в определенном состоянии, мы устанавливаем 1 для этого состояния. В противном случае ставим 0.

Каждая стрелка представляет собой «переход» из одного состояния в другое. Переход происходит один раз за каждый такт. В зависимости от текущего ввода мы можем каждый раз переходить в другое состояние. Обратите внимание на число в середине каждой стрелки. Это текущий ввод.

Например, когда мы находимся в состоянии «Initial-Stand by» и «читаем» 1, диаграмма говорит нам, что мы должны перейти в состояние «Activate Pulse». Если мы читаем 0, мы должны оставаться в состоянии «Initial-Stand by».

Итак, что именно делает наша «Машина»? Он запускается из состояния «Начальное - Ожидание» и ждет, пока на входе не будет считана 1. Затем он переходит в состояние «Активировать импульс» и передает на свой выход ВЫСОКИЙ импульс. Если кнопка остается нажатой, схема переходит в третье состояние, «цикл ожидания».

Там он ждет, пока кнопка не будет отпущена (вход становится 0), одновременно передавая на выходе LOW. Тогда все снова!

Возможно, это самая сложная часть процедуры проектирования, потому что ее нельзя описать простыми шагами. Чтобы построить диаграмму состояний, требуется опыт и немного острого мышления, но все остальное - это просто набор заранее определенных шагов.

Шаг 3

Затем мы заменяем слова, описывающие различные состояния диаграммы, на двоичные . числа. Нумерацию мы начинаем с 0, который присваивается начальному состоянию. Затем мы продолжаем перечисление с любым состоянием, которое нам нравится, пока все состояния не будут иметь свои номера. Результат выглядит примерно так:(рисунок ниже)

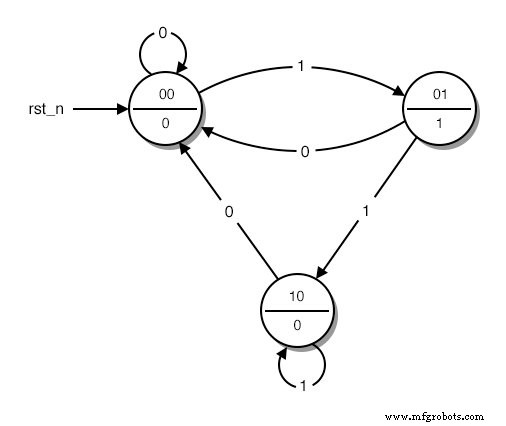
Диаграмма состояний с закодированными состояниями

Шаг 4

После этого мы заполняем Таблицу состояний . Эта таблица имеет очень специфическую форму. Я приведу таблицу нашего примера и воспользуюсь ею, чтобы объяснить, как ее заполнить (рисунок ниже)

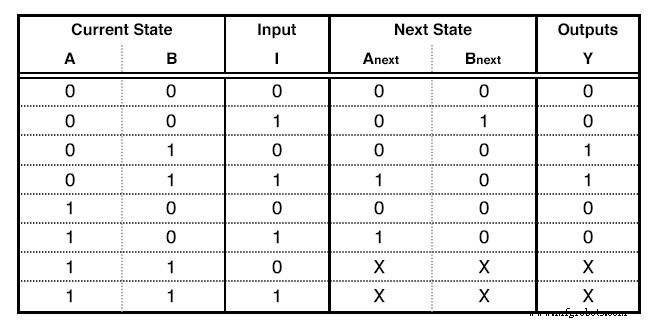
Таблица состояний

Первые столбцы равны битам наивысшего числа, которое мы присвоили диаграмме состояний. Если бы у нас было 5 состояний, мы бы использовали до 100, что означает, что мы использовали бы 3 столбца. В нашем примере мы использовали число до 10, поэтому нам понадобится всего 2 столбца. Эти столбцы описывают Текущее состояние нашей схемы.

Справа от столбцов "Текущее состояние" мы пишем Столбцы ввода . Их будет столько же, сколько и наших входных переменных. В нашем примере только один вход.

Затем мы пишем Столбцы следующего состояния . Их столько же, сколько столбцов "Текущее состояние".

Наконец, мы пишем Столбцы вывода . Это столько же, сколько и наших результатов. В нашем примере только один выход. Поскольку мы построили более конечный автомат, вывод зависит только от текущих состояний ввода. По этой причине в столбце output есть две единицы:для вывода логической функции, не зависящей от ввода I. Продолжайте читать, чтобы узнать подробности. Столбцы Current State и Input - это входы нашей таблицы. Заполняем их всеми двоичными числами от 0 до:

2 ^{(количество столбцов текущего состояния + количество столбцов ввода)} -1

К счастью, это проще, чем кажется. Обычно строк будет больше, чем фактических состояний, которые мы создали на диаграмме состояний, но это нормально.

Каждая строка столбцов следующего состояния заполняется следующим образом:мы заполняем ее состоянием, которого достигаем, когда на диаграмме состояний из текущего состояния той же строки мы следуем за входом той же строки. Если необходимо заполнить строку, номер текущего состояния которой не соответствует какому-либо фактическому состоянию на диаграмме состояний, мы заполняем ее условиями безразличия (X). В конце концов, нам все равно, куда мы можем уйти из несуществующего государства. Во-первых, нас бы там не было! Опять же, это проще, чем кажется.

Столбец выходов заполняется выходными данными соответствующего текущего состояния на диаграмме состояний.

Таблица состояний завершена! Он описывает поведение нашей схемы так же полно, как и диаграмма состояний.

Шаг 5а

Следующий шаг - взять эту теоретическую «Машину» и реализовать ее в схеме. Чаще всего в этой реализации используются шлепанцы. Это руководство посвящено этому типу реализации и описывает процедуру как для D-шлепанцев, так и для JK-шлепанцев. T - Вьетнамки не будут включены, так как они слишком похожи на два предыдущих случая. Выбор флип-флопа является произвольным и обычно определяется факторами стоимости. Наилучший выбор - выполнить как анализ, так и решить, какой тип триггера дает минимальное количество логических вентилей и меньшую стоимость.

Сначала мы рассмотрим, как мы реализуем нашу «Машину» с помощью D-шлепанцев.

Нам понадобится столько же D-Flip Flops, сколько столбцов State, в нашем примере 2. Для каждого триггера мы будем добавлять еще один столбец в нашу таблицу состояний (рисунок ниже) с именем входа триггера, в данном случае «D». Столбец, соответствующий каждому триггеру, описывает какие входные данные мы должны дать триггеру, чтобы перейти от текущего состояния к следующему состоянию . . Для D-триггера это просто:необходимый ввод равен следующему состоянию. В строках, содержащих X, мы также заполняем X в этом столбце.

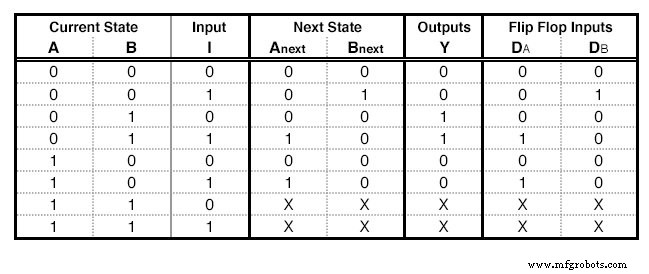
Таблица состояний с возбуждением D-триггера

Шаг 5б

Мы можем проделать те же шаги с JK - Flip Flops. Однако есть некоторые отличия. JK - Flip Flop имеет два входа, поэтому нам нужно добавить два столбца для каждого Flip Flop. Содержание каждой ячейки определяется таблицей возбуждения JK:

В этой таблице сказано, что если мы хотим перейти от состояния Q к состоянию Q _next , нам нужно использовать конкретный вход для каждого терминала. Например, чтобы перейти от 0 к 1, нам нужно скормить J с помощью 1, и нам все равно какой вход мы подаем на терминал К.

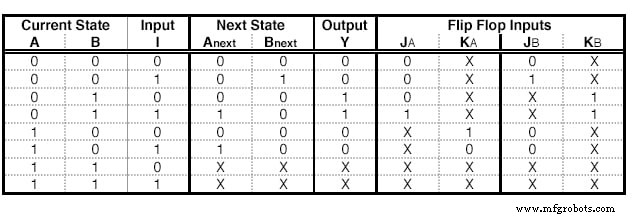
Таблица состояний с JK - Flip Flop Excitations

Шаг 6

Мы на завершающем этапе нашей процедуры. Остается определить логические функции, которые производят входные данные наших триггеров и выходных данных. Мы извлечем одну логическую функцию для каждого входного сигнала Flip Flop, который у нас есть. Это можно сделать с помощью карты Карно. Входными переменными этой карты являются переменные текущего состояния а также Входы.

Тем не менее, функции ввода для наших D-триггеров следующие:(рисунок ниже)

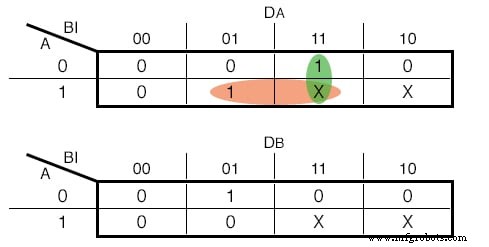
Карты Карно для входов D-триггера

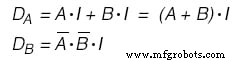
Если бы мы выбрали JK - Flip Flops, наши функции были бы следующими:(Рисунок ниже)

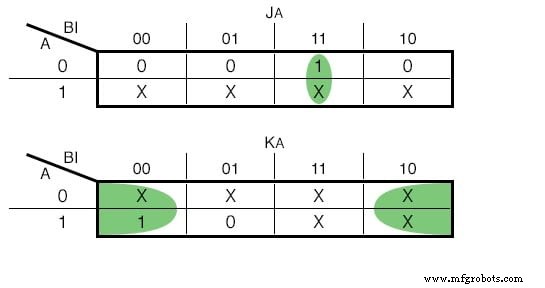
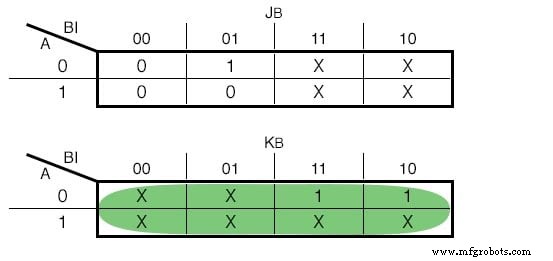
Карта Карно для JK - вход с триггером

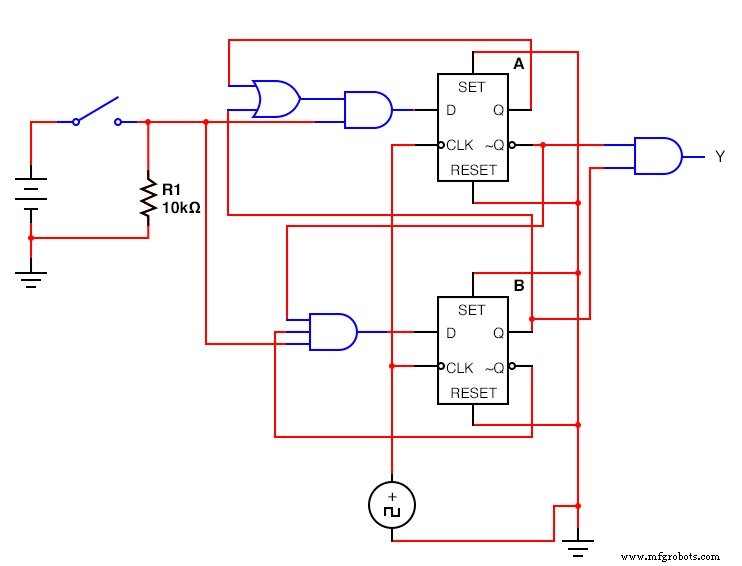
Карта Карно также будет использоваться для определения функции вывода:(рисунок ниже)

Карта Карно для выходной переменной Y

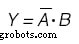
Шаг 7

Мы проектируем нашу схему. Мы размещаем триггеры и используем логические элементы для формирования вычисленных нами логических функций. Ворота принимают входные данные с выхода триггеров и входа схемы. Не забудьте подключить часы к шлепанцам!

Версия D - триггера:(рисунок ниже)

Завершенная последовательная схема D-триггера

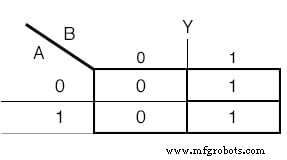
Версия JK - Flip Flop:(рисунок ниже)

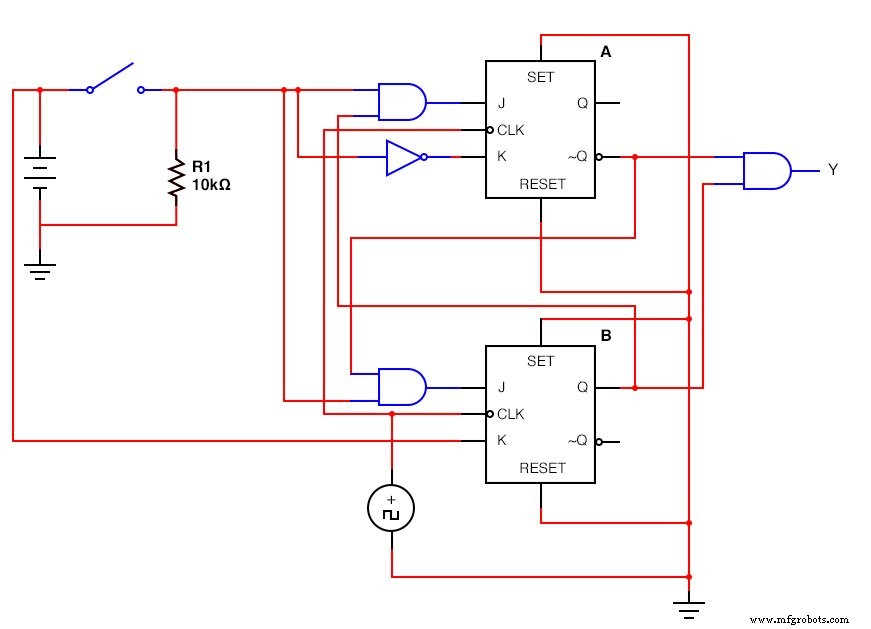
Завершенная JK - последовательная схема триггера

Это оно! Мы успешно спроектировали и построили последовательный контур. Сначала это может показаться сложной задачей, но после практики и повторения процедура станет тривиальной. Последовательные схемы могут пригодиться в качестве управляющих частей более крупных схем и могут выполнять любую последовательную логическую задачу, о которой мы только можем подумать. Небо это предел! (или хотя бы печатная плата)

ОБЗОР:

• Функция последовательной логики имеет функцию «памяти» и принимает во внимание прошлые входные данные, чтобы принять решение о выходе.
• Конечный автомат - это абстрактная математическая модель функции последовательной логики. У него конечные входы, выходы и количество состояний.
• Конечные автоматы реализуются в реальных схемах с помощью триггеров.
• Процедура реализации требует определенного порядка шагов (алгоритма) для выполнения.