Ячейки без заботы на карте Карно

До этого момента мы рассматривали задачи логической редукции, в которых входные условия были полностью заданы. То есть таблица истинности с тремя переменными или карта Карно имели 2 ⁿ =2 ³ или 8 записей, полная таблица или карта.

Для некоторых реальных проблем не всегда необходимо заполнять полную таблицу истинности. У нас может быть выбор не заполнять полную таблицу.

Например, при работе с числами BCD (двоично-десятичное кодирование), закодированными как четыре бита, нас могут не заботить какие-либо коды выше диапазона BCD (0, 1, 2… 9). 4-битные двоичные коды для шестнадцатеричных чисел (Ah, Bh, Ch, Eh, Fh) не являются допустимыми кодами BCD.

Таким образом, нам не нужно заполнять эти коды в конце таблицы истинности или K-карты, если нам это не нужно.

Обычно нам не нужно заполнять эти коды, потому что эти коды (1010, 1011, 1100, 1101, 1110, 1111) никогда не будут существовать, пока мы имеем дело только с числами в кодировке BCD. Эти шесть недействительных кодов наплевать что касается нас.

То есть нас не волнует, какой выходной сигнал выдает наша логическая схема, на это нас не волнует.

Не волнует

Неважно в карте Карно или в таблице истинности может быть либо 1 s или 0 s, до тех пор, пока нас не волнует, каков будет результат для входного условия, которое мы никогда не ожидаем увидеть. Мы отмечаем эти ячейки звездочкой * среди обычных 1 s и 0 с.

При формировании групп ячеек рассматривайте ячейку безразличия как 1 или 0 или игнорируйте безразличие.

Это полезно, если позволяет нам сформировать большую группу, чем это было бы возможно без безразличия. Нет необходимости сгруппировать все или часть безразличных действий.

Используйте их только в группе, если это упрощает логику.

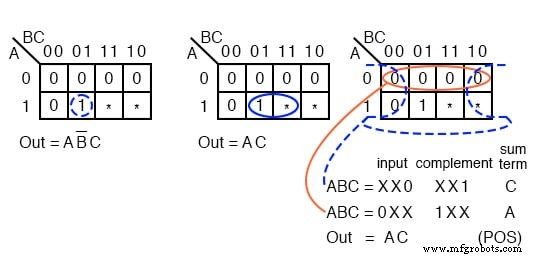
Выше приведен пример логической функции, где желаемый результат равен 1 . для ввода ABC =101 в диапазоне от 000 до 101 . Нас не волнует, каков будет результат для других возможных входов ( 110, 111) . . Сопоставьте этих двоих как безразличие. Мы показываем два решения.

Решение справа Out =AB’C является более сложным, поскольку мы не использовали ячейки без внимания. Решение посередине, Out =AC, менее сложно, потому что мы сгруппировали ячейку безразличия с одним 1 чтобы сформировать группу из двух человек.

Третье решение, произведение сумм справа, является результатом группировки безразличных элементов с тремя нулями, образующими группу из четырех 0 с. Это то же самое, менее сложное, Out =AC .

Мы показали, что клетки без заботы могут использоваться как 1 s или 0 s, в зависимости от того, что пригодится.

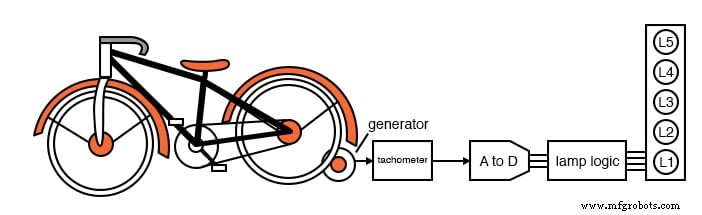
Класс электроники в Государственном колледже Лайтнинг попросили построить логику лампы для выставки стационарных велосипедов в местном научном музее. Когда гонщик увеличивает скорость вращения педалей, на гистограмме загораются лампы.

Ни одна лампа не загорится, если не будет движения. По мере увеличения скорости загорается нижняя лампа L1, затем L1 и L2, затем L1, L2 и L3, пока все лампы не загорятся с максимальной скоростью. Когда все лампы загорятся, дальнейшее увеличение скорости никак не повлияет на дисплей.

Небольшой генератор постоянного тока, подключенный к велосипедной шине, выдает напряжение, пропорциональное скорости. Он управляет платой тахометра, которая ограничивает напряжение на верхнем пределе скорости, когда горят все лампы. Никакое дальнейшее увеличение скорости не может увеличить напряжение выше этого уровня.

Это очень важно, поскольку нисходящий преобразователь A в D (аналого-цифровой) выдает 3-битный код ABC . , 2 ³ или 8-кодов, но у нас всего пять ламп. А самый старший бит, C младший значащий бит.

Логика лампы должна реагировать на шесть кодов от A до D. Для ABC =000 , ни движения, ни лампочек. Для пяти кодов (от 001 до 101) лампы L1, L1 и L2, L1, L2 и L3, вплоть до всех ламп, будут гореть по мере увеличения скорости, напряжения и кода от A до D (ABC).

Нас не волнует ответ на вводимые коды (110, 111) потому что эти коды никогда не выйдут из A в D из-за ограничения в блоке тахометра. Нам нужно разработать пять логических схем для управления пятью лампами.

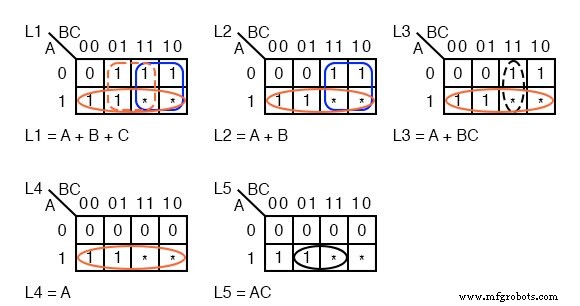
Поскольку ни одна из лампочек не горит в течение ABC =000 . от A до D введите 0 во всех K-картах для ячейки ABC =000 . Поскольку нас не волнуют никогда не встречающиеся коды (110, 111) , введите звездочки в эти две ячейки на всех пяти K-картах.

Лампа L5 будет гореть только при коде ABC =101 . . Введите 1 в этой ячейке и пять 0 s в оставшиеся пустые ячейки L5 K-карты.

L4 сначала загорится при коде ABC =100 . , и будет гореть, если код больше, ABC =101 , потому что все лампы ниже L5 загораются, когда горит L5. Введите 1 . s в ячейки 100 и 101 карты L4, чтобы он загорелся для этих кодов. Четыре 0 Заполняет оставшиеся ячейки L4

L3 сначала загорится при коде ABC =011 . . Он также загорается всякий раз, когда загораются L5 ​​и L4. Введите три 1 s в ячейки 011, 100, 101 для карты L3. Заполните три 0 s в оставшиеся ячейки L3.

L2 загорается для ABC =010 и коды больше. Заполните 1 s в ячейки 010, 011, 100, 101 , и два 0 s в остальных ячейках.

Единственный раз, когда L1 не горит, это отсутствие движения. Уже есть 0 в ячейке ABC =000 . Все остальные пять ячеек получают 1 . с.

Сгруппируйте 1 Как показано выше, использовать безразличие всякий раз, когда получается большая группа. На карте L1 показаны три термина продукта, соответствующие трем группам по 4 ячейки.

Мы использовали оба типа «безразлично» в двух группах и один «безразлично» в третьей группе. Безразличие позволило нам сформировать группы по четыре человека.

Подобным образом карты L2 и L4 создают группы из 4 клеток с помощью клеток без заботы. Уменьшение L4 поразительно тем, что лампа L4 управляется самым старшим битом аналого-цифрового преобразователя, L5 =A . .

Для лампы L4 не требуется никаких логических вентилей. На картах L3 и L5 отдельные клетки образуют группы из двух безразличных клеток. На всех пяти картах сокращенное логическое уравнение менее сложно, чем без безразличия.

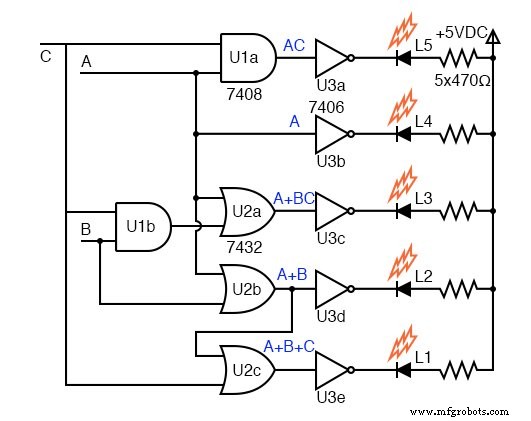
Схема ворот для схемы выше. Выходы пяти уравнений K-map управляют инверторами. Обратите внимание, что L1 ИЛИ гейт - это не вентиль с 3 входами, а вентиль с 2 входами, имеющий входы (A + B), C , вывод A + B + C открытый коллектор инверторы, 7406 , тем не менее, желательны для управления светодиодами, а не частью логической схемы K-карты.

Выход затвора с открытым коллектором или инвертора разомкнут на коллекторе, внутреннем по отношению к корпусу интегральной схемы, так что весь ток коллектора может протекать через внешнюю нагрузку. Активный высокий уровень на любом из инверторов подтягивает выходной низкий уровень, протягивая ток через светодиод и токоограничивающий резистор.

Скорее всего, светодиоды будут частью твердотельного реле, управляющего лампами на 120 В переменного тока для музейных экспонатов, которые здесь не показаны.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист схем цифрового дисплея
• Картографический лист Карно