Метод измерения параметров движения с несколькими степенями свободы на основе дифракционных решеток с перекрестной связью полидиметилсилоксана

Фон

Параметры движения с несколькими степенями свободы могут предоставить точную информацию о местоположении и ориентации конкретной цели, которая широко использовалась для больших конструкций в таких приложениях, как управление стабильностью ориентации самолета, стабильность прицеливания систем датчиков пушки, роботизированная рука. перемещение, выравнивание прецизионных деталей и позиционирование деталей для промышленной обработки [1,2,3].

Поэтому методы высокоточного обнаружения использовались для определения информации с несколькими степенями свободы (например, прямолинейности, тангажа и угла отклонения) о целях, и для этих методов требовались высокопроизводительные датчики, в том числе характеристики высокоскоростного обнаружения. , синхронизация, высокая точность измерения и в реальном времени. Эти методы широко использовались в аэрокосмической отрасли, в беспилотных летательных аппаратах, в точном производстве и в приложениях для оптической центровки [4,5,6].

Метод точного измерения в реальном времени и разделение динамической информации о движении с несколькими степенями свободы были ключевыми элементами для определения стабильности положения носителя. Hsieh [7] предложил трехмерную матрицу обнаружения, в которой использовались три группы модулей для обнаружения различных степеней свободы, в которых разные модули датчиков использовались для измерения различной информации о местоположении, а алгоритм использовался для вычисления угловых и многоуровневых измерений. информация о степенях свободы. Лю [8] представил метод измерения параметров движения с несколькими степенями свободы, основанный на изменении относительного угла между двумя сборными решетками для выполнения информационных измерений. Однако вышеупомянутый подход был подвержен ошибкам из-за сборки двух или более чувствительных элементов и сложности расчетов связи, а его точность также зависела от высокоточной приборной системы.

С развитием технологии производства микронано-нанотехнологий, нанотехнологий и наноматериалов исследователи изучили методы определения параметров движения с несколькими степенями свободы на основе однокристальной реализации с точки зрения миниатюризации и недорогого применения в области наноматериалов, оптических материалов и наноустройств. Тана [9] сообщил об алгоритме обнаружения параметров движения с несколькими степенями свободы с недифрагирующим лучом на основе портативной миниатюрной призменной конструкции, которая может минимизировать ошибки измерения. Наша команда представила метод векторного тензодатчика, основанный на единственном чувствительном элементе, который может быть применен для измерения поверхностной векторной деформации с использованием многоосных интегрированных механических датчиков, и послужил основой для исследований в этой статье [8, 10].

В этой работе был продемонстрирован метод измерения вектора смещения и угла с несколькими степенями свободы, основанный на одном элементе; Этот элемент был изготовлен с использованием технологии кислородно-плазменной обработки, чтобы сформировать структуру оптической решетки с ортогональным градиентом на обеих сторонах подложки из полидиметилсилоксана (PDMS), которая была предварительно изогнута в форму эллипса. Эти скрещенные оптические решетки могут вызывать дифракцию входного лазерного луча в двумерную матрицу пятен. Информация о местоположении дифракционного пятна может использоваться для достижения угла падения луча, рассчитанного алгоритмом определения местоположения в реальном времени. На основе этого метода и устройства с зарядовой связью (ПЗС) 480 × 640 пикселей разрешение измерения смещения и угла отклонения составляло 0,18 мкм и 0,0075 рад соответственно. Кроме того, ПЗС-матрица с более высокими пикселями может улучшить разрешение измерения смещения и угла отклонения до субнанометрового и микрорадианного уровней соответственно. Наконец, с помощью предложенного метода отслеживалось динамическое положение парящего винтокрылого аппарата в режиме реального времени; полученная информация может быть использована для корректировки положения корабля, и это доказывает новый метод стабилизации самолета в небе.

Экспериментальный

Приготовление полидиметилсилоксана (PDMS)

PDMS (Sylgard 184) был приобретен у Dow Corning. Мембраны из ПДМС (10:1) были приготовлены методом центрифугирования на кремниевых пластинах и отверждены сразу после центрифугирования при температурах менее 80 ° C в течение 2 часов. Подложки PDMS толщиной 600 мкм были приготовлены путем регулирования скорости прядения.

Подготовка двойной ортогональной решетки

В соответствии с требованиями эксперимента были изготовлены пленки ПДМС площадью 3 × 3 см ² . . Затем пленки PDMS были предварительно растянуты относительно оригинала в 1,5 раза по оси X с использованием самодельной трансляции. Морщинистый SiO _x затем были сформированы слои на O ₂ предварительно напряженный субстрат PDMS, подвергнутый плазменной обработке (IoN Wave 10, PVA-TePla, Германия), в условиях расхода кислорода 30 см3 / мин и времени окисления 40 с. Ровные и упорядоченные структуры с нанорешетками формировались на поверхности подложки PDMS после релаксации предварительного напряжения. Как показано на рис. 1а, этот процесс был повторен на другой стороне подложки PDMS с угловой разницей 90 °, чтобы сформировать ортогональные решетчатые структуры с обеих сторон подложки PDMS.

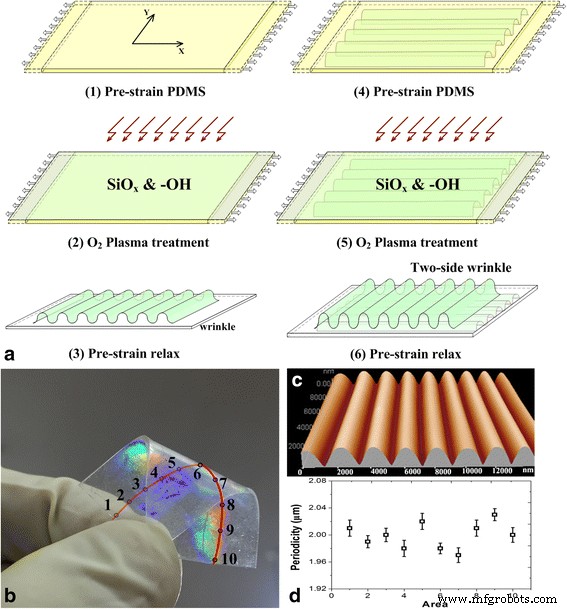
Характеристики процесса изготовления и морфологии двойной оптической решетки PDMS. а Изготовление двойной оптической решетки. б Оптические изображения решетки. c Изображение решетки с помощью атомно-силовой микроскопии. г Равномерность периодичности для выборок

Создание тестовой платформы

Система датчика угла смещения с четырьмя степенями свободы включает в себя лазерный источник света, узел платформы для измерения угла и смещения, держатель образца, экран, камеру CCD и компьютер. Как показано на рис. 2a, гелий-неоновый лазерный источник света (длина волны лазера 680 нм) был установлен в узле поворотно-смещенной платформы, который состоял из электрической вращающейся платформы и рамы для ручной трехмерной регулировки (Beijing Zolix Instrument Co., Ltd .). Платформа имеет точность вращения 0,1 ° и точность перемещения 2 мкм. Эта пересекающаяся оптическая решетка может вызвать дифракцию лазерного луча в двумерную матрицу пятен. Дополнительная камера металл-оксид-полупроводник (CMOS) с разрешением 480 × 640 пикселей использовалась для получения изображения двумерного массива пятен в реальном времени с использованием алгоритмов обработки изображений MATLAB, которые использовались для извлечения местоположения каждой точки дифракции и последующего вычисления x- и y -смещения осей и информация об углах. Была предоставлена ​​испытательная площадка в виде четырехвинтового самолета (Typhoon Q500, Yuneec Electric Aviation). И информация о четырех степенях свободы была получена для получения положения парения в помещении.

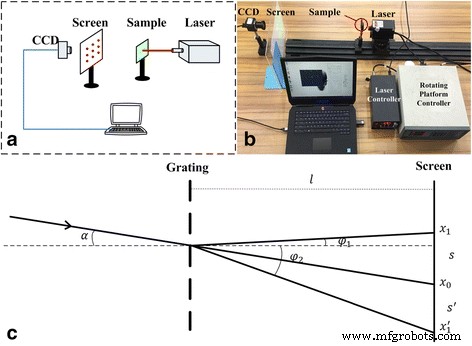
Принцип и система тестирования для параметра движения MODF. а схема системы. б Настройка системы. c Принцип проверки смещения и угла

Анализ и обсуждение

Характеристика ортогональной решетки PDMS

Процесс изготовления показан на рис. 1а. При гидрофильной модификации поверхности ПДМС использовалась кислородно-плазменная технология. SiO _x Таким образом, на предварительно изогнутых подложках PDMS с помощью кислородной плазмы образовывались гидрофильные группы (например, -OH). Когда предварительная деформация в подложке PDMS превышает критическое значение, решетчатые структуры на поверхности PDMS формировались после релаксации предварительной деформации [11, 12]. Периодичность решеток была достигнута настройкой применяемых условий предварительного изгиба и плазмы и может быть рассчитана в наших предыдущих работах. Как показано на рис. 1с, топографии микро- / нанорешеток были охарактеризованы с помощью атомно-силовой микроскопии (АСМ) (CSPM5500; Benyuan Co.). Как показано на рис. 1b, d, вдоль центральной линии на одной стороне образца было выбрано 10 участков для исследования периодичности и однородности решетчатых структур. Соответствующая периодичность решеток из 10 участков была равномерной и имела период (2 ± 0,05) мкм по всей поверхности образца.

Дифракционная решетка для определения параметров позиционного и углового движения

Согласно теории дифракции Фраунгофера [13], лазерный луч проходит мимо образца (с решеткой) и дифрагирует в матрицу световых пятен. Положение дифракционного пятна напрямую связано с положением и углом падающего луча, и, таким образом, информация о положении падающего луча может быть обнаружена с помощью информации о местоположении дифракционных пятен.

На рис. 2 показана движущаяся и вращающаяся платформа для отслеживания положения и соответствующих дифракционных пятен падающего луча. Согласно теории дифракции Фраунгофера, когда дифракционная решетка и расстояние до экрана фиксированы, то соотношение между падающим лучом, дифрагированным лучом и длиной волны может быть выражено следующим образом:

Здесь λ была длина волны падающего луча, d был период решетки, α угол падения, φ был угол дифракции, а м порядок дифракции на решетке.

Когда угол падения α не было равно 0, «+» означает, что дифракционный луч и падающий луч распределены на одной стороне нормали решетки, а «-» указывает, что дифракционный луч и падающий луч существуют по две стороны от нормали. При определенном угле падения расстояния между точками дифракции первого и нулевого порядка на экране не были равны. Следовательно, расстояние между точками может меняться в зависимости от угла падения. Угол падающего луча можно рассчитать количественно путем расчета положения дифракционного светового пятна. Одновременно подвижное расположение падающего луча вызывает перемещение нулевого порядка точки дифракции. Информация о положении падающего луча может быть вычислена по информации о местоположении нулевого порядка точки дифракционного луча.

На рисунке 2c показано одно направление дифракционной диаграммы решетки, где x ₀ был первым порядком дифракционных пятен, а x ₁ и \ ({x} _1 ^ {\ hbox {'}} \) обозначают второй порядок дифракционных пятен. Из рис. 2c, s и s ’- расстояние между дифракционными пятнами первого и второго порядка, которое выражалось следующим образом:

Из уравнения. (1):

Исходя из вышеизложенного, модель корреляции между углом падения луча и расстоянием между дифракционными спеклами может быть получена как:

Обнаружение и определение параметров движения с несколькими степенями свободы на основе ортогональной дифракционной решетки

Лазерный луч, проходящий через одностороннюю оптическую решетку, может образовывать одиночные дифракционные пятна. Ортогонально ориентированный элемент может быть сформирован, когда лазерный луч проходит через ортогональные решетки на двух сторонах подложки PDMS. Одномерный дифракционный луч решетки будет сформирован, когда световой луч будет передан вдоль направления решетки на одной стороне экрана, и размеры были установлены в x -ось. Затем формировался пучок одномерной дифракционной решетки, перпендикулярный оси x -axis, когда световой луч проходит по направлению решетки на другой стороне экрана, а затем размер был установлен в y -ось. На экране был сформирован двумерный массив точек дифракции, как показано на рис. 3b.

Параметр движения MODF зависит от перемещения дифракционных пятен. а Одномерные дифракционные пятна создавались однонаправленной решеткой. б Двумерный массив пятен создавался двойной поперечной оптической решеткой. c Перемещение массива пятен контролировалось перемещением лазерного источника. г Зазор, перемещающийся между решеткой пятен, контролировался как угол падения лазерного луча

Когда положение лазерного луча было изменено, нулевой порядок положения дифракционного светового пятна покажет соответствующее движение, и положение дифракционного растрового изображения изменится соответствующим образом на основе теории дифракции Фраунгофера. Положение падающего луча может быть непосредственно вычислено на основе направления движения решетки, а затем обнаружена информация о реализации положения светового луча вдоль x- и y -ось. Как показано на рис. 3c, первый порядок положения точки дифракции не может точно рассчитать смещение света из-за эффектов связи смещения и отклонения. Кроме того, нулевой порядок расположения точек дифракции был связан только с расположением источника. Следовательно, было бы более точно использовать нулевой порядок смещения точки дифракции для вычисления положения источника света. Как показано на рис. 3d, информация об угле отклонения падающих световых лучей вдоль x ось и y -ось может быть рассчитана по расстоянию между световыми пятнами на x ось и y -ось на основе связанной модели между углом и изменением пятна.

Однако ограничение причины смещения дифракционных пятен зависит от угла падения и расстояния между решеткой и экраном согласно формуле. (1). В наших работах решетка крепилась к экрану, то есть разброс расстояния между решеткой и экраном был равен нулю. При перемещении лазерного источника по z дифракционные пятна не смещались. -ось. Также, когда лазерный источник вращался по z -оси изменение угла падения равнялось нулю, что не привело бы к смещению дифракционных пятен.

В наших экспериментах изменение угла (Δ θ _x ) вдоль x -ось может быть рассчитана с точки зрения расстояния между столбцами ( s _x , \ ({s} _x ^ {\ hbox {'}} \)) дифракционных пятен и изменение угла (∆ θ _y ) вдоль y -ось может быть рассчитана на основе расстояния между столбцами ( s _y , \ ({s} _y ^ {\ prime} \)) дифракционных пятен. Платформа портфолио была настроена для изменения местоположения источника света, а затем изображения камеры были получены программным обеспечением MATLAB каждые 0,02 с для извлечения положения дифракционных пятен для сравнения с более ранними значениями, которые использовались для расчета смещений массива пятен на х ось и y -оси, а также изменения расстояния между столбцами и строками в массиве.

На основе алгоритма смещение массива пятен может быть проанализировано путем обработки изображения до и после перемещения для вычисления ∆ x , ∆ y , ∆ θ _x , и ∆ θ _y . Поскольку лазерное пятно включает в себя несколько пикселей в изображении, а его энергия соответствует гауссовскому распределению, для удаления фонового шума из изображения и точного определения местоположения центра лазерного пятна использовался метод подгонки гауссова распределения. Функция Гаусса лазерного пятна выражается следующим образом:

Вот, Я ( x , y ) была интенсивностью пятна, а H была амплитуда, ( x ₀ , y ₀ ) - координаты центра светового пятна, а σ ₁ , σ ₂ были стандартными отклонениями на x ось и y -оси соответственно.

К обеим сторонам приведенного выше уравнения можно применить логарифм, чтобы получить местоположение центра пятна, которое можно выразить следующим образом:

Здесь a , b , c , и d были полиномиальными коэффициентами, которые были получены с помощью гауссовой аппроксимации всех пикселей в пятне.

Изменения расстояния между двумя дифракционными пятнами были рассчитаны по двум изображениям до и после движения. А центральное пятно дифракционных пятен задано как система координатных центров перед движением:системы координат абсолютного и относительного перемещения светового пятна. Система координат абсолютного смещения дифракционного светового пятна взяла за основу неподвижный экран. Информация о движении ( Δx , Δy ) решетки на обоих экранах можно рассчитать по нулевому порядку координаты точки дифракции (то есть по положению центра). Система координат относительного смещения для светового пятна взяла нулевой порядок дифракционного пятна в качестве эталона, который можно использовать для расчета изменений расстояния между пятнами и решетками ( S _x ) и расстояние между рядами ( S _y ).

На рисунке 4 показана характеристика четырех степеней свободы. Когда лазерный луч косил вдоль x -оси, имело место соответствующее движение дифракционной решетки в x -axis, но смещение было около нуля в y -ось. Чувствительность смещения составляла около 5,4 пикселя / мкм. Этот метод можно использовать для расчета информации о местоположении источника света вдоль оси с высокой точностью, как показано на рис. 4а.

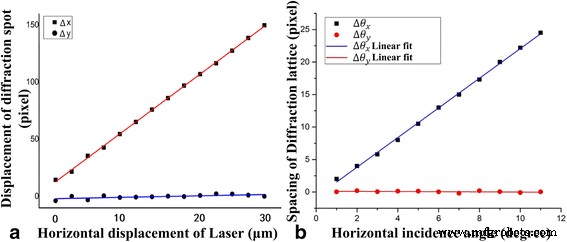
Характеристика четырех степеней свободы. а Смещение лазерного источника зависит от смещения дифракционных пятен. б Угол падения лазерного источника зависит от зазора между дифракционными пятнами

Когда лазер повернулся на небольшой угол вдоль x -оси, произошло соответствующее изменение расстояния между рядами дифракционных пятен и решеток, и расстояние между столбцами дифракционных пятен было равно нулю. Чувствительность смещения составляла около 2,3 пикселя на угол (/ °). Между тем, диапазон измерения угла составлял около 9,8 °, теоретически рассчитанный по формулам. (1) - (5) как расстояние s =0. Отнесение к первому порядку дифракционных пятен совпадает с нулевым порядком дифракционных пятен, поскольку при увеличении угла падения изменение расстояния между дифракционными пятнами будет равно нулю ( s =0). Этот метод можно использовать для получения информации об угле источника света вдоль x -ось. Информация о местоположении и ракурсе также может быть получена с помощью этого метода.

Разрешение обнаружения в один пиксель зависит от алгоритма, основанного на программном обеспечении MATLAB. Как вычислено выше, метод имеет чувствительность к смещению 5,4 пикселя / мкм, что означает разрешение 0,18 мкм . Для чувствительности к смещению 2,3 пикселя / ° , это было разрешение 0,0075 рад. Это показывает, что на основе представленного здесь метода и разрешения ПЗС разрешение смещения и угла составляло 0,18 мкм и 0,0075 рад соответственно. ПЗС-матрица 480 × 640 пикселей использовалась для получения изображения двумерной матрицы пятен в реальном времени. Кроме того, ПЗС-матрица с большим количеством пикселей и оптимизация светового пути могут улучшить разрешение смещения и угла отклонения до субнанометрового и микрорадианного масштабов соответственно.

Описание информации о параметрах движения несущего винта летательного аппарата

Винтокрылый летательный аппарат был разновидностью гражданской беспилотной летательной системы с низкой точностью, которая широко использовалась в авиации, авиамоделизме и навигации. Контроль устойчивости винтокрылого аппарата представляет собой микромир беспилотной боевой платформы. Для реализации высокоточного управления полетом наиболее важным аспектом было устойчивое управление ориентацией и положением самолета. И основным аспектом было декодирование высокоточной информации о положении и положении при зависании в реальном времени, так что точная информация о параметрах движения с четырьмя степенями свободы при зависании становится важным преимуществом.

В нашем эксперименте, основанном на перекрестно-связанной дифракционной решетке, был представлен метод измерения для получения информации об ориентации полета самолета с четырьмя степенями свободы в реальном времени. Во-первых, самолет с четырьмя винтами был использован для замены платформы, которая была составлена ​​из положения и положения испытательной системы с четырьмя степенями свободы, которая была основана на двойной решетке для установки четырех степеней свободы. -система проверки ориентации на свободу для четырехвинтовых самолетов. В испытательной системе небольшая лазерная указка была закреплена в центре четырехвинтового самолета в качестве источника света, и она направляла лазерные лучи вертикально вниз. Образец с двойной решеткой, экраном и камерой разворачивается по центру оптической оси. Эта пересекающаяся оптическая решетка может вызвать дифракцию лазерного луча в двумерную матрицу пятен. В экспериментах камера использовалась для получения изображения с экрана и передачи изображений на компьютер в реальном времени для вычисления информации о смещении с помощью программного обеспечения MATLAB.

Чтобы добиться быстрых, точных измерений сигналов полета в режиме реального времени, четырехвинтовой самолет завис в воздухе и быстро отслеживал сигнал положения, сохраняемый в течение 4 с. Информация об осевых перемещениях по x ось и y -оси для четырехвинтового самолета были получены за время 4 с, как показано на рис. 5c. На основе установления плоской системы координат (т. Е. x -ось и y -ось), x и y значения конвертируются в эти координатные точки. 200 результатов позиционирования за 4 секунды означают, что одна точка была получена за 0,02 секунды. Это представляет собой использование метода слежения за самолетом каждые 0,02 с в реальном времени для определения его местоположения и местоположения. Самолет имеет максимальное смещение 2,1 мм в x ось и максимальное смещение 2,3 мм по оси y -ось, согласно алгоритму.

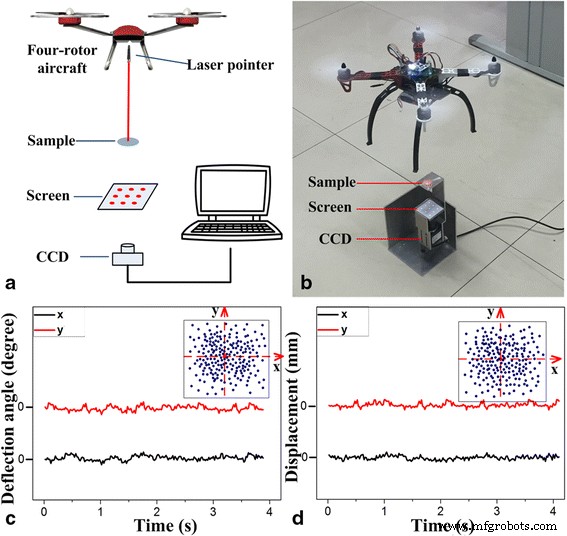
Характеристики отношения четырехвинтового корабля. а Схема системы. б Настройка системы. c Угол отклонения винтокрылого аппарата. г Водоизмещение винтокрылого аппарата

Кроме того, информация об угле тангажа и угле крена для летательного аппарата была рассчитана с помощью вышеуказанного алгоритма и способа обработки данных. Как показано на вставке к рис. 5d, точечная диаграмма угла поворота самолета с четырьмя винтами доставляла точную информацию об угле для самолета путем отслеживания в реальном времени каждые 0,02 с. Было замечено, что самолет имеет максимальное угловое отклонение 1 ° в x -ось и y- ось. Таким образом, с помощью этого метода можно вычислить информацию о четырех степенях свободы для самолета, которая может передавать точные сигналы местоположения и угла в систему управления полетом в течение 0,02 с для повышения устойчивости самолета.

Выводы

Таким образом, была продемонстрирована простая технологическая технология изготовления ортогональной оптической решетчатой ​​структуры с периодичностью 2 мкм на двух сторонах подложки PDMS. На основе структуры ортогональной оптической решетки был изучен способ идентификации положения луча и информации о параметрах углового движения с использованием информации о положении дифракционного светового пятна на основе эффекта дифракции Фраунгофера. ПЗС-матрица размером 480 × 640 пикселей использовалась для получения изображений двумерной матрицы пятен в реальном времени. Результаты показывают, что при использовании этого метода и описанной выше ПЗС-матрицы разрешение смещения и угла отклонения составляло 0,18 мкм и 0,0075 рад соответственно. Кроме того, с более высокой пиксельной ПЗС-матрицей разрешение смещения и угла отклонения может улучшиться до субнанометрового и микрорадианного масштабов соответственно. Этот метод может использоваться для определения точных положений наведения и информации об угле несущего винта самолета в реальном времени с высокой точностью каждые 0,02 с. Информация может возвращаться для управления системой полета беспилотных летательных аппаратов в воздухе. Этот метод был простым, недорогим и высокоточным. Он позволял осуществлять мониторинг в реальном времени, обеспечивая при этом исследовательскую основу для стабильного полета и точного управления летательными аппаратами для беспилотных боевых платформ.