Высококачественные двухзонные резонансы Фано, индуцированные двойными связанными состояниями в континууме с использованием плоской пластины с нанотверстиями

Введение

Улучшение взаимодействия между светом и веществом, которое имеет большое значение для улучшения характеристик оптических устройств, может быть реализовано за счет использования высококачественных (Q) -факторных откликов [1]. Резонанс Фано, характеризующийся асимметричной формой линий и резким спектральным профилем, обеспечивает эффективный подход для достижения высокой добротности в оптических метаматериалах и получил большое внимание [2]. В последнее десятилетие о резонансе Фано сообщалось во многих системах осцилляторов нанометрового размера, обеспечиваемых плазмонными наноструктурами [3, 4], где резонанс Фано возбуждается поверхностным плазменным резонансом на границе раздела металл-диэлектрик. Хотя металлические метаматериалы являются многообещающими кандидатами для манипуляции со светом, резонанс Фано в плазмонных метаматериалах обычно страдает низкой добротностью в видимой и ближней инфракрасной (БИК) областях спектра из-за присущих металлу омических потерь.

С другой стороны, полностью диэлектрические метаматериалы обеспечивают сильные резонансы типа Ми с индуцированными токами смещения, подобные таковым в плазмонных метаматериалах, но имеют меньшие диссипативные потери в видимом и ближнем ИК диапазоне [5]. Энергия падающего света может быть сильно локализована в диэлектрических наноструктурах из-за возбуждения электрических и / или магнитных диполярных резонансов, что снижает диссипативные потери и обеспечивает значительное резонансное усиление как электрического, так и магнитного полей. В последние годы связанные состояния в континууме (BIC) стали наиболее многообещающей схемой для достижения откликов с высокой добротностью в полностью диэлектрических метаматериалах [6, 7]. BIC находятся внутри непрерывного спектра расширенных состояний, но, как это ни парадоксально, остаются идеально локализованными в пространстве с теоретически бесконечным временем жизни [8, 9]. Хотя BIC не наблюдаются из непрерывного спектра из-за неизлучающего свойства, резонансы Фано с высокой добротностью могут быть достигнуты, поскольку BIC преобразуются в квази-BIC (QBIC) [10, 11], потенциальные применения включают, например, направленные генерация [12], оптические фильтры [13], нелинейное преобразование частоты [14], сверхчувствительные датчики [15, 16] и оптические вихревые пучки [17].

Как правило, формирование BIC тесно связано с симметрией (в плоскости и вертикальной симметрии) фотонной структуры из-за ее интерференционной природы. Более конкретно, BIC могут быть возмущены посредством наклонного падения или наноструктур с нарушенной симметрией, а QBIC могут быть реализованы, когда канал излучения между собственными состояниями и свободным пространством открыт [18, 19]. Однако большинство диэлектрических наноструктур, используемых для возбуждения QBIC с высокой добротностью, сложны, такие как асимметричные нанокрестики [20], асимметричные нанокольца [21], асимметричные наностержни [22,23,24] и асимметричные наностержни [25,26, 27,28], которые сложно изготовить из-за необходимости вставки глубоких субволновых щелей [20,21,22,23,24] или наноотверстий [25,26,27,28] в фотонные структуры. Другие наноструктуры, такие как прямоугольные стержни измененной формы [29, 30], имеют увеличенные острые края, что затрудняет их точное изготовление с помощью обычных литографических методов, что снижает добротность и резонансный срок службы устройств из-за открытия дополнительные негерметичные каналы [31, 32]. Более того, наклонные наноструктуры [33, 34], другой тип структур, испытывают трудности с точным контролем ориентации нанополос с глубокими субволновыми пространствами между резонаторами, поддерживаемыми в процессе нанопроизводства. В приложениях имеет смысл реализовать BIC и резонансы Фано с высокой добротностью, используя полностью диэлектрические метаматериалы с более простой архитектурой, такие как наноструктурированные планарные плиты [35,36,37,38]. Кроме того, множественные резонансы Фано очень полезны в таких приложениях, как усиление генерации многополосных гармоник [39], многоканальное зондирование [40] и излучение света [41]. Таким образом, получение множественных резонансов Фано с высокой добротностью дает существенное преимущество при использовании сравнительно простой архитектуры, основанной на возбуждении QBIC.

В этой работе предлагается новая плоская плита с нанотверстиями (PNS), состоящая из тетрамеризованных отверстий, для достижения двухзонных резонансов Фано с высокой добротностью. Сжимая или расширяя тетрамеризованные отверстия PNS по диагоналям сверхрешетки, возбуждаются два QBIC, и положение двух резонансов Фано, а также их добротность можно гибко настраивать. Множественные разложения в дальнем поле и распределения сверхрешетки в ближнем поле выполняются, чтобы выявить резонансные особенности PNS, что указывает на то, что двухзонные резонансы Фано являются результатом резонансного взаимодействия между электрическими тороидальными диполями или магнитными тороидальными диполями. Двухдиапазонный резонанс Фано PNS обладает поляризационно-независимым свойством, и они могут сохраняться даже при значительном изменении геометрических параметров PNS, что делает его более подходящим для потенциальных приложений.

Методы

Структура и дизайн решетки

На рис. 1 показана схематическая геометрия предлагаемой ПНС и ее спектры пропускания. ПНС состоит из четырех наноотверстий, которые можно сжимать (Δ <0) или расширять (Δ> 0) с расстоянием сдвига Δ по диагоналям сверхрешетки, а Δ =0 соответствует простой решетке с периодом, уменьшенным вдвое, где каждое наноотверстие находится в центре четверти площади сверхрешетки. Период и высота PNS равны Λ и H соответственно; радиус наноотверстия r . Показатель преломления PNS составляет n _s =3,2, а фон - воздух с показателем преломления n _а =1. На рисунке 1c показаны спектры PNS в зависимости от расстояния сдвига Δ, где PNS освещается нормально падающим x -поляризованный свет. Спектры, а также распределения электромагнитного поля PNS, представленные в этой статье, рассчитаны с использованием коммерческого программного обеспечения COMSOL Multiphysics для метода конечных элементов. Как показано на рис. 1c, для неусаженной ПНС с Δ =0 резонанса Фано нет. Однако два резонанса Фано со 100% глубиной модуляции (определяемой как разность пропускания между пиками Фано и провалами Фано) могут быть получены с помощью слегка усаживая или расширяя наноотверстия. По сравнению с ответом передачи сжатой PNS, ответ передачи сжатой PNS резко меняется, в то время как боковые полосы остаются почти такими же.

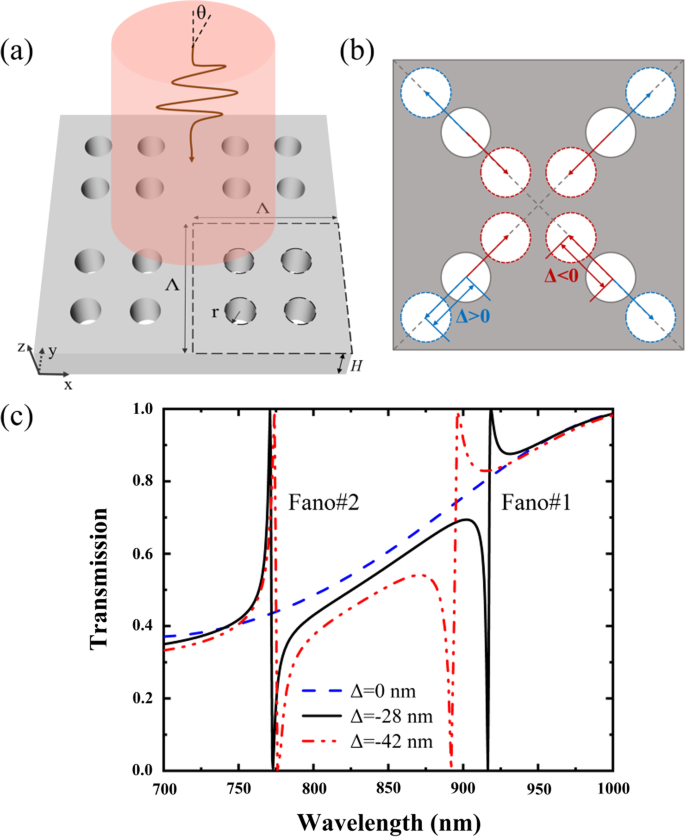
а Перспективный вид ПНС. б Вертикальный вид ПНС в виде четырех наноотверстий, которые сжимаются (Δ <0) или расширяются (Δ> 0) по диагоналям сверхрешетки. c Спектры пропускания PNS в зависимости от расстояния сдвига Δ. PNS находится под освещением x -поляризованная падающая волна с углом падения θ =0. Параметры ПНС:Λ =350 нм, r =35 нм и H =175 нм

Чтобы ясно показать эволюцию двухзонных резонансов Фано, возникающих из-за сжатия или расширения тетрамеризованных дырок, 2D-карта пропускания PNS в зависимости от расстояния сдвига Δ показана на рис. 2a. Как показано на рис. 2а, два BIC возникают в интересующей области длин волн, поскольку Δ =0, и подобное явление двойных BIC ранее сообщалось в структурах метамембран с двойной решеткой [13] и разъемного кольцевого резонатора [21]. В случае Δ ≠ 0 реализуются двухзонные резонансы Фано, поскольку BIC индуцируются в QBIC из-за нарушения симметрии PNS, то есть от центросимметрии простой решетки к четырехкратной вращательной (C ₄ ) симметрия сверхрешетки. Кроме того, поскольку C ₄ Симметрия PNS может поддерживаться по мере того, как тетрамеризованные дырки сжимаются или расширяются по диагоналям сверхрешетки, спектры пропускания PNS одинаковы для одного и того же абсолютного значения | Δ |. В принципе, сжатие или расширение тетрамеризованных отверстий уменьшает площадь первой зоны Бриллюэна PNS, поскольку элементарная ячейка PNS изменяется от простой решетки к сверхрешетке, а защищенный симметрией BIC может возбуждаться при нормальном падении из-за внесение поверхностных возмущений, а также сворачивание зоны Бриллюэна ПНС [42, 43]. Как правило, добротность BIC с защитой от симметрии показывает обратную квадратичную зависимость от степени асимметрии δ на основе теории возмущений [21]:

где ĸ - константа пропорциональности, S - площадь сверхрешетки, ω - угловая частота, а параметр асимметрии равен \ (\ delta {=} \ sqrt 2 \ Delta / \ Lambda \).

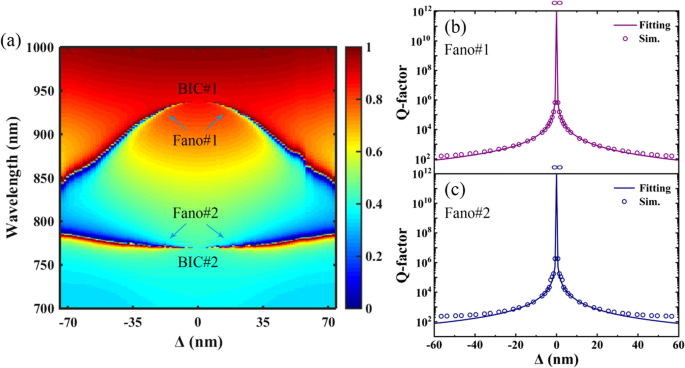
а 2D-карта пропускания PNS как функция расстояния сдвига Δ по диагоналям сверхрешетки. б и c Добротность и результат аппроксимации Фано № 1 и Фано № 2 соответственно. Остальные параметры такие же, как на рис. 1c

На рис. 2b, c показаны Q-фактор и результат подгонки для Фано № 1 и Фано № 2, соответственно. Добротность PNS рассчитывается как отношение резонансной длины волны λ _r и его полная ширина на полувысоте (FWHM) Δλ, где Δλ - область длин волн между пиком и провалом резонанса Фано. Результаты подгонки PNS рассчитываются с использованием уравнения. (1). Как показано на рис. 2b, c, расходящиеся траектории PNS, где добротности расходятся до бесконечности при Δ =0, подтверждаются с помощью отношения обратных квадратов для соответствия данным. Могут быть получены отличные результаты подгонки, и небольшое расхождение при большей асимметрии связано с отклонением от предположения о крошечном возмущении в уравнении. (1). Существенным преимуществом PNS является то, что расположение и добротность двухдиапазонных резонансов Фано можно настроить путем сжатия или расширения тетрамеризованных отверстий, что облегчает динамическое управление резонансными характеристиками многократного сигнала с высокой добротностью. Резонансы Фано.

Физические механизмы и интерпретация

Чтобы понять происхождение двухзонных резонансов Фано посредством сжатия или расширения тетрамеризованных отверстий PNS, мы разложим излучение дальнего поля BIC и резонанса Фано на вклады различных мультипольных компонентов для дальнейшего обсуждения их особенностей. Мультипольные моменты могут быть рассчитаны на основе плотности тока смещения j в сверхрешетке ПНС [26, 44, 45]:

где P , M , Т , Q ^{( e )} и Q ^{( м )} - моменты электрического диполя (ED), магнитного диполя (MD), тороидального диполя (TD), электрического квадруполя (EQ) и магнитного квадруполя (MQ) соответственно; c - скорость света в вакууме, а α , β = x , y , z . Здесь плотность заряда ρ , которая обычно встречается в определениях ED и MQ, была заменена на плотность тока смещения j через соотношение сохранения заряда \ (i \ omega \ rho + \ nabla \ cdot {\ varvec {j}} =0 \). В случае гармонического возбуждения ~ exp ( iωt ), рассеивающая способность индуцированных мультипольных моментов, вносящих вклад в ответ в дальней зоне, может быть записана как:

где первые два члена соответствуют обычному рассеянию ЭД (заряда) и МД. Третий член соответствует ПД-рассеянию. Четвертый и пятый члены происходят от EQ и MQ. Последний член - это член более высокого порядка, который содержит многопольное рассеяние высокого порядка и связь между ними, и им, как правило, можно пренебречь. Используя уравнения. Используя формулы (2) - (7), можно получить вклады различных мультиполей в рассеивающую способность дальнего поля.

На рис. 3 показана рассеивающая способность разных мультиполей ДНС для разного расстояния сдвига Δ, остальные параметры такие же, как на рис. 1в. Как показано на рис. 3a – d, для PNS с Δ =0, ED и MD являются доминирующими диполями, и они не являются резонансными в интересующей области длин волн. Однако путем сжатия или расширения наноотверстий ПНС с | Δ | ≠ 0 могут быть реализованы двухзонные резонансы Фано из-за возбуждений резонансных дипольных мод. Чтобы ясно увидеть важную роль резонансных дипольных мод в формировании наблюдаемых двухзонных резонансов Фано, на рис. 3e, f показана нормализованная рассеивающая способность различных мультиполей с Δ =- 28 нм вокруг Fano # 1 и Fano # 2, соответственно. . Как показано на рис. 3e, доминирующими резонансными модами являются ED и TD вокруг Фано № 1, а Фано № 1 является прямым следствием резонансной связи электрических тороидальных диполей. В частности, ED и TD сильно увеличиваются до сопоставимой величины на резонансной вершине (918,5 нм) Fano # 1; таким образом, 100% передача может быть получена из-за деструктивной интерференции между ED и TD. В то время как для резонансного провала (916,5 нм) Фано № 1 отражение увеличивается до максимума, а пропускание стремится к нулю из-за усиленного рассеяния ED и TD. Точно так же, как показано на рис. 3f, Fano # 2 возникает из-за резонансной связи магнитных тороидальных диполей, его вершина (771,1 нм) указывает на деструктивную интерференцию между MD и TD, а его наклон (772,9 нм) связан с усиленное рассеяние MD и TD. Обратите внимание, что из-за сильной связи электрических тороидальных диполей или магнитных тороидальных диполей, резонансные моды устойчивы как для Фано № 1, так и для Фано № 2, даже если Δ изменяется.

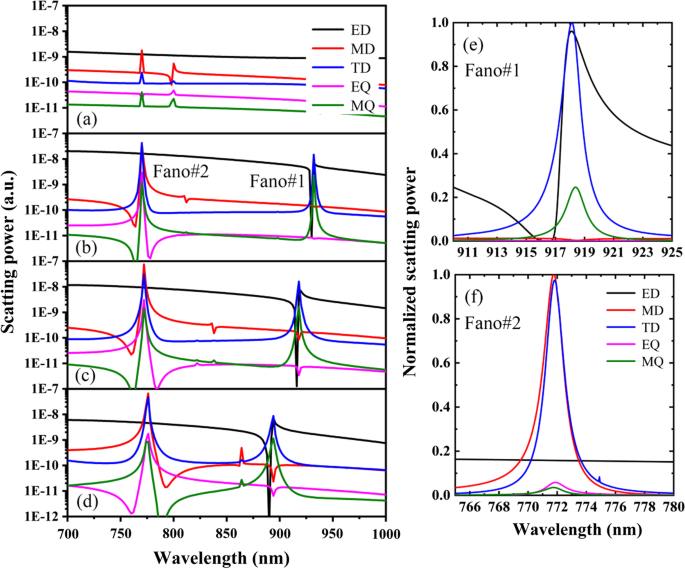
Рассеивающая способность декартовых ED, MD, TD, EQ и MQ при a Δ =0, b Δ =- 14 нм, c Δ =- 28 нм и d Δ =- 42 нм. е и е Нормированная рассеивающая способность различных мультиполей с Δ =- 28 нм вокруг Фано № 1 и Фано № 2 соответственно. Остальные параметры такие же, как на рис. 1c

Чтобы связать реакцию передачи двухзонных резонансов Фано в дальней зоне с возбуждением индуцированных мультипольных моментов, на рис. 4 показаны распределения электромагнитного поля и тока смещения резонансов Фано сверхрешетки ПНС. На рис. 4а, б электрическое поле Фано №1 хорошо удерживается в сверхрешетке ПНС с током смещения вдоль x ось, указывающая на резонансный режим ЭД. Более того, ток смещения Fano # 1 образует две перевернутые петли между центром и краями сверхрешетки, а магнитное поле образует петлю в yz плоскости, соответствующей TD-резонансной моде вдоль x ось [44, 46]. Следовательно, Fano # 1 возникает из-за резонансной связи между модами ED и TD, которые соответствуют прогнозируемым результатам мультипольных разложений, как упомянуто выше. Фактически, из-за резонансных характеристик электрических тороидальных диполей Fano # 1, распределения электромагнитного поля и тока смещения в резонансном пике (918,5 нм), центральной длине волны (917,5 нм) и резонансном падении (916,5 нм) Fano №1 почти такие же, за исключением небольшой разницы в амплитуде поля (дополнительный файл 1:Рис. S1). В случае Fano # 2, как показано на рис. 4c, электрическое поле сильно усиливается, и ток смещения формирует две обратные петли между центром сверхрешетки и соседней сверхрешеткой PNS, что указывает на режим резонанса TD вдоль г ось. Кроме того, магнитное поле Фано № 2 сильно локализовано в сверхрешетке с направлением вдоль y ось, показанная на рис. 4d, с резонансным режимом MD. В результате Fano # 2 является прямым следствием резонансной связи магнитных тороидальных диполей, что согласуется с предсказанием мультипольных разложений дальнего поля PNS. Кроме того, из-за связи магнитных тороидальных диполей Fano # 2 электромагнитное поле и ток смещения на резонансном пике (771,1 нм), центральной длине волны (772,0 нм) и резонансном падении (722,9 нм) Fano # 2 показывают аналогичные дистрибутивов (дополнительный файл 1:рисунок S2).

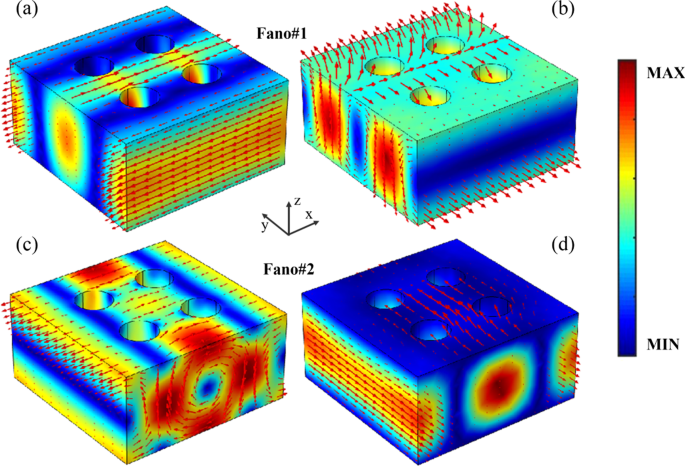
Распределения электромагнитного поля и тока смещения резонансов Фано сверхрешетки ПНС, цветная полоса представляет амплитуду поля, а красные стрелки указывают вектор поля или вектор тока смещения. Остальные параметры такие же, как на рис. 1в, с Δ =- 28 нм. а и c Распределения амплитуды электрического поля и вектора тока смещения Фано № 1 и Фано № 2 соответственно. б и d Распределения амплитуды магнитного поля и вектора магнитного поля Фано № 1 и Фано № 2 соответственно

Результаты и обсуждение

На рисунке 5 показаны спектры пропускания PNS в зависимости от радиуса r . наноотверстия, а остальные параметры такие же, как на рис. 1в с Δ =- 28 нм. Как показано на рис. 5а, двухдиапазонный резонанс Фано может поддерживаться как r изменяется от 0 до максимального значения 67,5 нм, т.е. , тетрамеризованные дырки касаются друг друга в сверхрешетке. Увеличение радиуса нанотверстия r увеличивает поверхностные возмущения PNS и снижает его эффективный показатель преломления (ERI), что приводит к увеличению добротности и синему смещению резонансов Фано. В частности, резонансное расположение Фано №1 более чувствительно к изменению r , и двухзонные резонансы Фано имеют тенденцию сливаться в одну резонансную моду по мере приближения тетрамеризованных дырок друг к другу. Как показано на рис. 5b, увеличение r не только смещает в синий цвет резонансное положение резонансов Фано, но также увеличивает их полуширину. Как r увеличивается с 25 до 45 нм, резонансные пики Fano # 1 и Fano # 2 смещены в синий цвет с 936,7 нм и 793,2 нм до 887,6 нм и 743,8 нм соответственно; и их FWHM увеличиваются с 0,8 нм и 0,6 нм до 6,8 нм и 3,1 нм соответственно. Обратите внимание на увеличение r также улучшает глубину модуляции резонансов Фано, а 100% глубина модуляции может быть реализована как r больше 30 нм. Кроме того, оценивая сдвиг длины волны пика Фано, на который влияют структурные параметры PNS, показано, что радиус наноотверстия r является наиболее чувствительным структурным параметром как для Фано № 1, так и для Фано № 2 (Дополнительный файл 1:Рисунок S3). Следовательно, вариант r обеспечивает эффективный подход к динамическому управлению резонансными характеристиками двухдиапазонных резонансов Фано PNS.

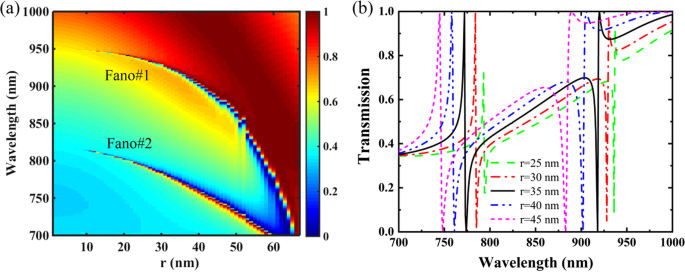
а 2D-карта передачи PNS как функция радиуса r наноотверстия. б Спектры пропускания ПНС для различного радиуса наноотверстия r . Остальные параметры такие же, как на рис. 1в с Δ =- 28 нм

На рисунке 6 показано влияние симметрии конструкции на характеристики передачи PNS, где радиус r ' двух наноотверстий варьируется от нуля до касательной друг к другу, а остальные параметры такие же, как на рис. 1в с Δ =- 28 нм. Как показано на рис. 6а, для сверхрешетки с зеркальной симметрией вдоль x ось (направление электрического поля падающего света), как радиус r 'Двух наноотверстий увеличивается, резонансные положения двухзонных резонансов Фано смещены в синюю сторону из-за уменьшения ERI PNS, а их ширина полосы расширяется из-за увеличения поверхностных возмущений. Однако, как показано на рис. 6b, хотя два резонанса Фано могут поддерживаться с увеличением r ′, Два дополнительных резонанса Фано возникнут как зеркальная симметрия сверхрешетки вдоль x ось сломана. В общем, нарушение структурной симметрии вдоль x ( г ) также нарушит симметрию режима вдоль оси x ( г ) оси периодической решетки, а безызлучательная невырожденная мода способна взаимодействовать с внешним излучением благодаря своей вырожденной составляющей [47]. Следовательно, тот факт, что два дополнительных резонанса Фано присутствуют только для структуры с нарушенной зеркальной симметрией вдоль x ось указывает, что они вызваны возмущенными невырожденными модами.

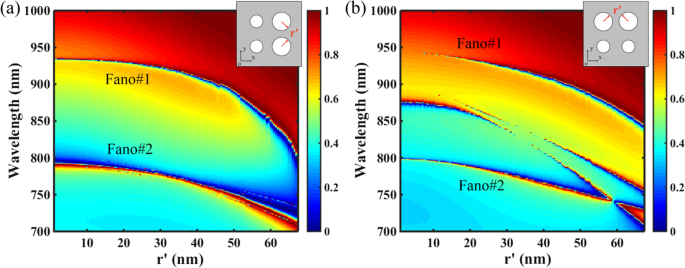
Влияние симметрии структуры на характеристики передачи PNS. Остальные параметры такие же, как на рис. 1в, с Δ =- 28 нм. На вставках изображена принципиальная схема сверхрешетки ПНС. а 2D-карта передачи PNS как функция радиуса r ′ Двух наноотверстий, где структурная симметрия сверхрешетки вдоль x ось сохраняется. б 2D-карта передачи PNS как функция радиуса r ′ Двух наноотверстий, где структурная симметрия сверхрешетки вдоль x ось сломана

Далее мы охарактеризовали резонансные характеристики PNS под влиянием угла падения и угла поляризации. Как показано на рис. 7a, двухдиапазонный резонанс Фано PNS невосприимчив к изменению угла поляризации из-за C ₄ симметричная топология. Поскольку угол поляризации изменяется от 0 до 90 °, то есть от x -поляризация на y -поляризация, Фано № 1 и Фано № 2 остаются неизменными. Однако в случае угла падения, как показано на рис. 7b, хотя Fano # 1 также нечувствителен к изменению угла падения, Fano # 2 смещается в красную сторону, поскольку угол падения отклоняется от нормального, и возникает дополнительный резонанс Fano. (Фано № 3) происходит из-за подавления радиационного распада защищенного симметрией BIC, которое отменяется при падении с отклонением от нормы. В общем, этот тип подавления распада излучения BIC тесно связан с деструктивной интерференцией между полями испускаемого излучения от двух встречных вытекающих мод на любом из двух краев стоп-зоны периодических решеток [48]. Обратите внимание, что из-за сильной связи между Фано № 2 и Фано № 3 в соседней области между ними может быть возбуждено узкое окно наведенной прозрачности.

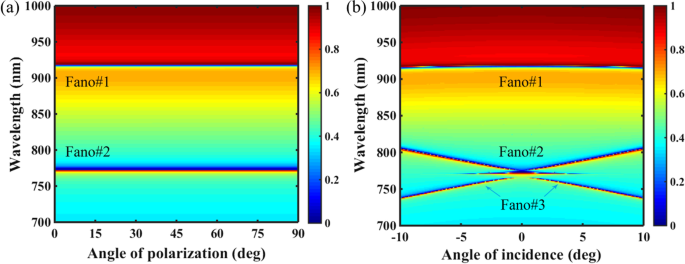
а 2D-карта пропускания PNS как функция угла поляризации. б 2D-карта пропускания PNS в зависимости от угла падения. Остальные параметры такие же, как на рис. 1в с Δ =- 28 нм

Наконец, мы показали, что множественные резонансы Фано могут быть получены за счет увеличения высоты H плиты PNS. На рис. 8 показана двумерная карта пропускания PNS в зависимости от H для неусадочной (Δ =0 нм) и усадочной (Δ =- 28 нм) структур. Как показано на рис. 8а, при изменении H нет резонанса Фано, за исключением резонансов Фабри – Перо (F – P) для несжатой ПНС. Согласно теории F – P, состояние резонанса полости F – P безусадочной ПНС можно записать как:

где δ - фазовый сдвиг, λ длина волны в свободном пространстве, n _эфф - ЭОП эквивалентной однородной плиты ДНС, φ - дополнительная фаза и м целое число, указывающее порядок резонанса. Используя теорию эффективной среды [49], ERI PNS можно оценить как:

где f - коэффициент заполнения PNS, а f =1–4π ( r / Λ) ² .

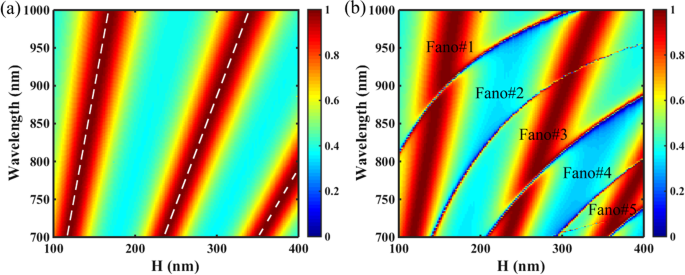
а 2D-карта пропускания PNS в зависимости от высоты плиты H с Δ =0 нм, белые пунктирные линии - результаты модели полости F – P. б 2D-карта пропускания PNS в зависимости от высоты плиты H с Δ =- 28 нм. Остальные параметры такие же, как на рис. 1c

Используя уравнения. (8) и (9), местоположения F – P-резонанса безусадочной ПНС можно рассчитать как λ _{F – P} =2 π · H · n _эфф / ( mπ - φ ). В расчете, хотя дополнительная фаза φ нельзя рассматривать как константу, потому что это явно влияет на фазовый сдвиг δ , его значения могут быть вычислены с помощью метода линейной аппроксимации [50, 51]. На рис. 8а показана двумерная карта пропускания ПНС с Δ =0 нм, а результаты теории F – P обозначены белыми пунктирными линиями. Как показано на рис. 8a, белые пунктирные линии модели полости F – P совпадают с линиями пиков пропускания PNS, подтверждая, что именно резонанс F – P улучшает передачу неусаженных PNS в пространстве. спектральная область интереса. Однако, как показано на рис. 8b, для усеченной ПНС с Δ =- 24 нм возбуждаются пять резонансов Фано с высокой добротностью, которые сосуществуют с резонансами F – P, когда H изменяется в диапазоне 100–400 нм. , резонансы Фано настолько сильны, что они расщепляют резонансы F – P в области пересечения между резонансами Фано и F – P. Согласно теории пластинчатого волновода, увеличение толщины пластины фотонного кристалла обеспечивает большее количество вытекающих мод, ограниченных в структуре [32, 52]; таким образом, количество резонансов Фано может быть увеличено простым увеличением толщины PNS. Обратите внимание, что сдвиг тетрамеризованных отверстий не изменит ERI PNS, таким образом, расположение резонансов F – P остается почти одинаковым как для неусадочной, так и для усадочной структур.

Выводы

High-Q-factor dual-band Fano resonances can be realized by using a comparatively simple architecture of PNS based on the excitation of dual QBICs. By shrinking or expanding four nanoholes of the PNS along the diagonals of the superlattice, two symmetry-protected BICs can be transformed to dual-band Fano resonances and their locations as well as their Q-factors can be flexibly tuned. The dual-band Fano resonances of the PNS are resulted from the resonant couplings between the electric toroidal dipoles or the magnetic toroidal dipoles, and their correlations between the far-field multiple decompositions and the near-field distributions of the superlattice are verified. The dual-band Fano resonances of the PNS possess polarization-independent feature, and their high-Q-factor features are robust to the variations of the geometric parameters. By increasing the height of the PNS, the number of high-Q-factor Fano resonances can be improved as more leaky modes can be supported by the structure. Our results give more tuning freedoms for the realization of high-Q-factor resonators with better performances, which may provide a further step in the development of lasing, sensing and nonlinear photonics.

Доступность данных и материалов

Наборы данных, использованные и / или проанализированные в ходе текущего исследования, доступны у соответствующего автора по разумному запросу.

Сокращения

Q-factor:

Quality factor

PNS:

Planar nanohole slab

BICs:

Bound states in the continuum

NIR:

Near-infrared

QBICs:

Quasi-BICs

FWHM:

Полная ширина на половине максимальной

ED:

Электрический диполь

MD:

Магнитный диполь

TD:

Toroidal dipole

EQ:

Электрический квадруполь

MQ:

Магнитный квадруполь

ERI:

Effective refractive index

F–P:

Fabry–Pérot