Преобразование звезды в дельту и дельты в звезду. Преобразование Y-Δ

Преобразование звезды в дельту и дельты в звезду — преобразование Y-Δ

В электрической сети импеданс может быть подключен в различных конфигурациях. Наиболее распространенными из этих конфигураций являются сеть, соединенная звездой или треугольником. Чтобы решить сложные электрические сети или упростить их, мы используем метод преобразования звезда-треугольник. Он заменяет любую сеть с подключением по схеме «звезда» эквивалентной сетью с подключением по схеме «треугольник» и наоборот. Мы собираемся предоставить краткую формулу для преобразования нагрузки между нагрузкой, соединенной звездой и треугольником.

Преобразование "звезда-треугольник"

Мы знаем основы последовательного, параллельного или комбинированного последовательного и параллельного соединения, но Y-Δ — это еще одна немного сложная конфигурация компонентов. Трехфазные сети состоят из трех проводов и обычно подключаются по схеме звезда-треугольник. . Трехфазное питание или нагрузка, подключенная в любой конфигурации, может быть преобразована в эквивалентную. Мы используем такое преобразование для упрощения математических расчетов, необходимых для анализа цепей сложной электрической сети.

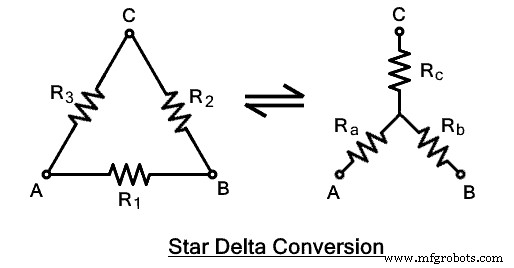
Дельта-подключенная сеть

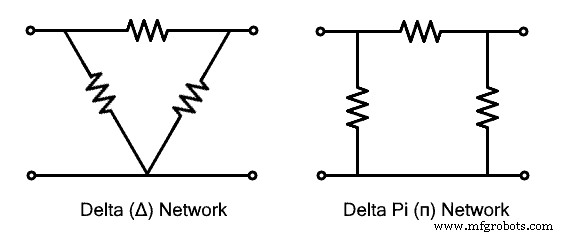
Сеть, соединенная треугольником, формируется, когда три ветви сети или импедансы соединяются в петлю таким образом, что их головки соединяются с хвостами соседней ветви. Полученная сеть образует форму треугольника, напоминающую греческую букву дельта «Δ», поэтому она и названа в ее честь. Она также известна как сеть π (пи), потому что она напоминает букву после перестановки ветвей. Узнайте больше о Delta Connection в предыдущем посте.

Подключенная сеть Star

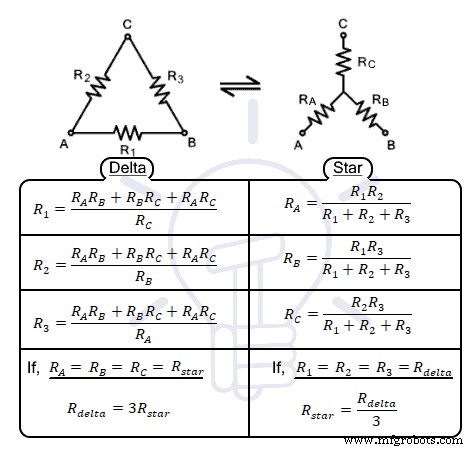
Сеть, соединенная звездой, формируется, когда три ответвления или импеданса соединяются вместе в общей точке. Остальные концы филиальных сетей свободны. Полученная форма напоминает букву «Y», поэтому ее также называют сетью, соединенной «Y» или «звездой». Она также известна как сеть с Т-образным соединением из-за ее формы после перестановки ветвей сети. Узнайте больше о Star Connection в предыдущем посте. 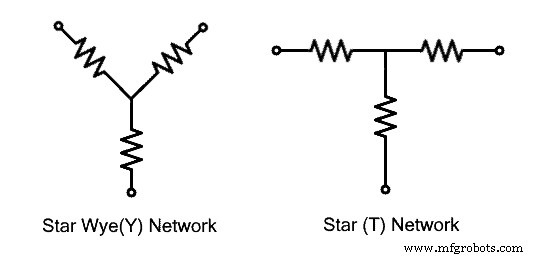Приведенные выше схемы можно преобразовать с помощью следующего преобразования. Во время преобразования клеммы A, B, C должны оставаться в том же положении, меняется только импеданс и их расположение. Следующий рисунок иллюстрирует приведенное выше утверждение.

Преобразование дельты в звезду

Сеть, соединенную треугольником, можно преобразовать в конфигурацию звезды с помощью набора электрических формул. Выведем уравнение для каждого импеданса. 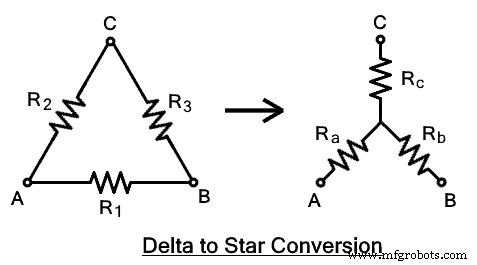На данном рисунке показана дельта-сеть с выводами A, B, C с импедансами R_{1 , R2 , R3 . Эквивалентная сеть со звездообразным соединением с RA , РБ &RC где они подключены к соответствующим клеммам, как показано на рисунке.}

Как упоминалось ранее, клеммы A, B, C остаются прежними, как и импеданс между ними, должен оставаться прежним.

Общий импеданс между AB в дельта-сети; 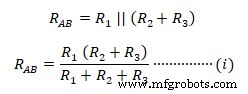Аналогично импеданс между клеммами B-C 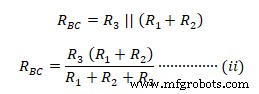Аналогично импеданс между A-C 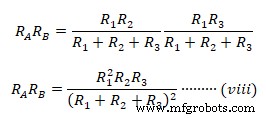Согласно звездной сети;

R_AB =Р_А + Р_Б

R_BC =Р_В + R_С

R_AC =Р_А + R_С

Складываем уравнения (i), (ii) и (iii) вместе. 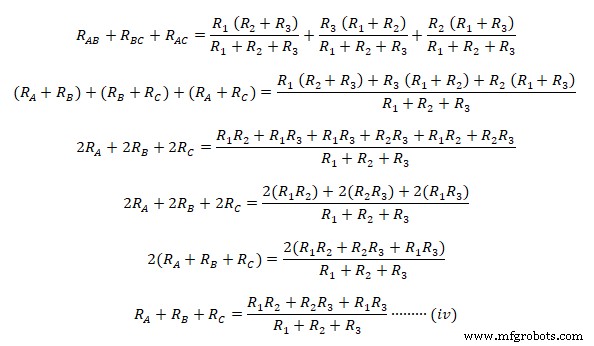Теперь вычтите уравнения (i), (ii) и (iii) одно за другим из уравнения (iv)

Сначала вычтите (ii) из (iv) 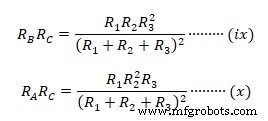Аналогичное вычитание (i) и (iii) из (iv) приводит к 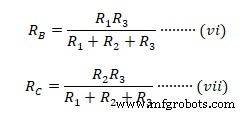Из полученных уравнений для звездообразных импедансов R_A , Р_Б , &R_С мы можем сделать вывод о связи между преобразованиями дельта-звезда как; эквивалентный импеданс звезды равен произведению импедансов соседних треугольников с конечным делением на сумму всех трех импедансов треугольника.

В случае, если все три импеданса одинаковы в дельта-сети эквивалентное сопротивление звезды станет

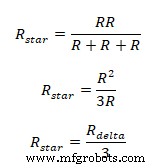Поскольку все импедансы в дельта-сети равны, каждые три эквивалентных сопротивления звезды будут в 1/3 раза больше дельта импеданс.

Преобразование со звезды на треугольник

Теперь мы собираемся преобразовать импеданс, соединенный звездой, в импеданс, соединенный треугольником. Давайте выведем уравнения, используемые для преобразования звезды в треугольник.

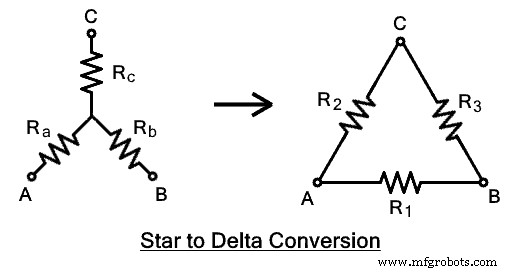На данном рисунке показано сопротивление соединения звездой R_A , Р_Б &R_К. В то время как требуемый дельта-эквивалентный импеданс составляет R₁ , R₂ &R₃ как показано на рисунке.

Чтобы найти эквивалентное дельта-сопротивление, умножьте предыдущее уравнение (v) и (vi), а также (vi) &(vii) &(v) &( vii) вместе.

 Умножение (v) и (vi) 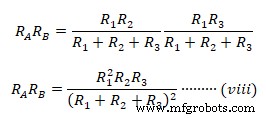Аналогично умножение (vi) на (vii) и (v) на (vii)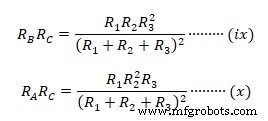

Теперь сложите уравнения (viii), (ix) и (x) вместе. 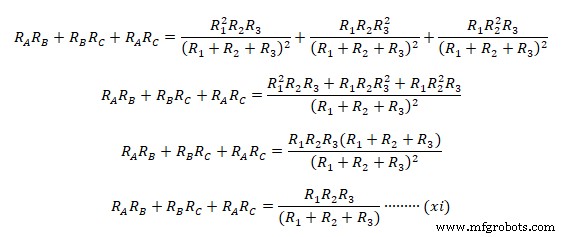Чтобы получить индивидуальный эквивалентный дельта-импеданс, мы разделим уравнение (xi) на (v), (vi ) и (vii) отдельно, например.

Деление (xi) на (v) 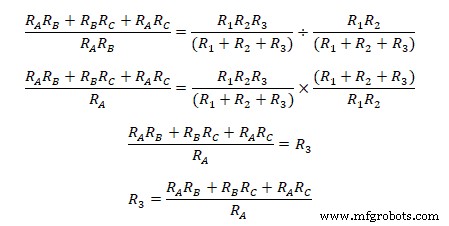Аналогичное деление уравнения (xi) на (vi) и (vii) по отдельности дает

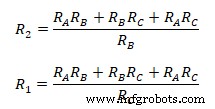Соотношение между эквивалентным импедансом звезды и треугольника ясно из данного уравнения. Сумма двойного произведения всех импедансов звезды, деленная на импеданс звезды соответствующего терминала, равна импедансу треугольника, связанного с противоположным терминалом.

Упрощение уравнений приведет к 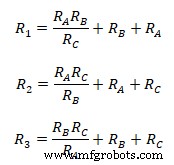В случае, если все импедансы звезд равны, эквивалентный импеданс треугольника будет;

Используя предыдущее уравнение,

Это уравнение предполагает, что каждое эквивалентное сопротивление треугольника в 3 раза больше сопротивления звезды.