Анализ схемы SUPERNODE | Шаг за шагом с решенным примером

Анализ суперузла — Заявление , формула и пошаговый пример решения

Что такое анализ суперузлов?

Сегодня мы попытаемся ответить на распространенный вопрос о том, почему мы используем анализ схем суперузлов. в то время как мы можем упростить схему с помощью простого анализа узлов или узловых цепей. .

В предыдущей статье мы обсудили, почему мы используем анализ цепей суперсетки . вместо использования простого анализа сетки для упрощения схемы. Если вы поняли этот момент, то это тот же случай с дискуссией. Если вы не удовлетворены, позвольте мне попытаться объяснить это на следующем примере.

Рассмотрите обе схемы на следующем рис. 1. Вы заметили что-то другое?

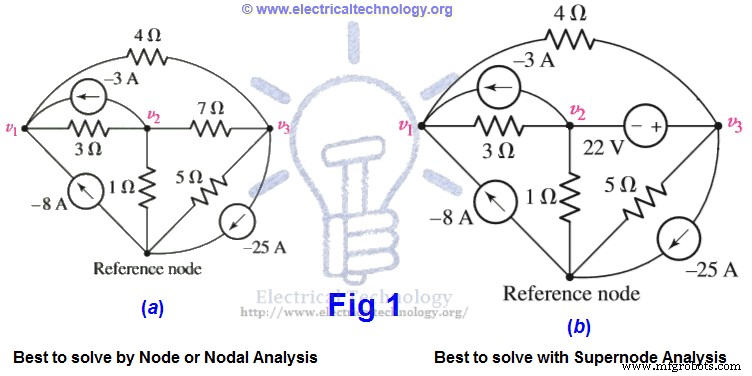
Разница в обеих схемах заключается в том, что дополнительный источник напряжения 22В вместо резистора 7Ом между узлом 2 и узлом 3. И это главное.

В Node или Узловой анализ , мы применяем KCL (закон тока Кирхгофа) к каждому небазисному узлу, т. е. мы применяем простой KCL сразу к трем узлам на рис. 1(a).

Если мы сделаем то же самое, т. е. применим анализ узлов вместо анализа цепей надузлов к схеме на рис. 1 (b), мы столкнемся с некоторыми трудностями в узле 1 и узле 2, потому что мы не знаем, какой ток в ветке с источником напряжения? Кроме того, нет такого способа, которым мы регулируем ситуацию, т.е. мы не можем выразить ток как функцию напряжения, где определение источника напряжения заключается в том, что напряжение не зависит от тока. Из-за этих трудностей и проблем мы используем анализ схемы суперузла вместо анализа узлов на приведенном выше рис. 1 (b).

Есть два способа упростить схему на рис. 1 (b) выше.

Первый ^й один, более сложный, состоит в том, чтобы присвоить неизвестное значение тока ветви, содержащей источник напряжения. Затем трижды примените KCL к 3 узлам (по одному уравнению KCL для каждого узла). Наконец, примените KVL (закон напряжения Кирхгофа), который равен v ₃ <сильный> – в ₂ =22 В между узлом 2 и узлом 3. В этом случае мы получаем четыре (4) уравнения для неизвестных значений в приведенном выше примере, который немного сложно упростить.

Второй ^й метод проще, чем описанный выше метод, который называется анализом суперузлов. В этом методе мы рассматриваем узел 2, узел 3 и источник напряжения 22 В вместе как своего рода суперузел и применяем KCL к обоим узлам (узлу 2 и узлу 3) одновременно.

Суперузел обозначается областью, обведенной пунктирной линией. Это возможно, потому что, если общий ток, выходящий из узла 2, равен нулю (0), а общий ток, выходящий из узла 3, равен нулю (0), то общий ток, выходящий из комбинации, равен нулю. Эта концепция показана на следующем рис. 2 (b) с суперузлом (область, обведенная пунктирной линией).

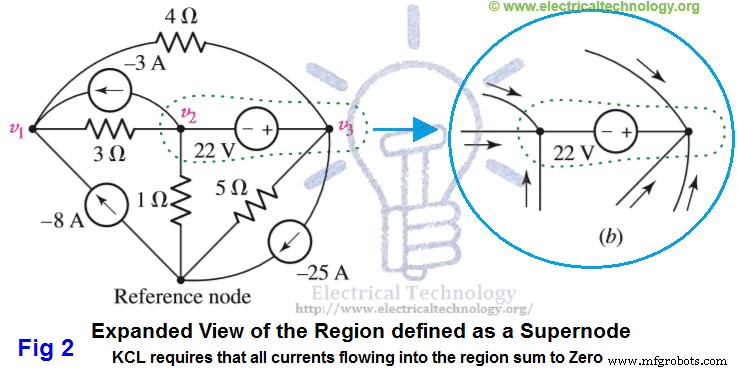
Теперь мы шаг за шагом решим приведенную ниже схему. пошаговый анализ схемы суперузла, а затем мы суммируем весь анализ суперузла (шаг за шагом).

• Похожая запись:анализ цепей SUPERMESH | Шаг за шагом с решенным примером

Пример анализа суперузла

Пример:

Используйте анализ суперузла, чтобы найти напряжение на каждом источнике тока, т. е. v ₁ &v ₂ на следующем рис. 3 (а)?

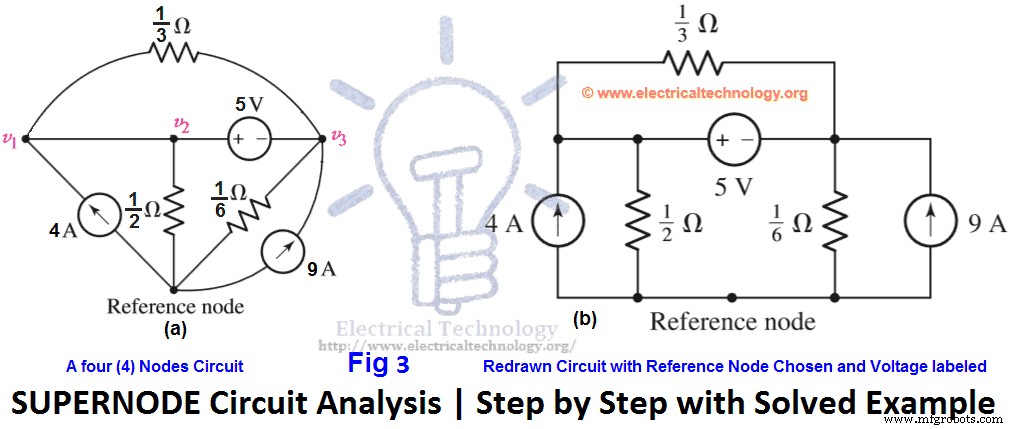
Решение:

Во-первых, мы перерисовываем схему, как показано на рис. 3(b).

Начнем с написания уравнения KCL для узла 1.

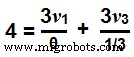
4 =0 + 3v ₁ + 3в ₃ …  → Уравнение 1.

Теперь рассмотрим суперузел (комбинация узлов Node1 и Node2). Причем подключены один источник тока и три резистора. Таким образом,

Применить KCL к суперузлу (Node1 и Node2)

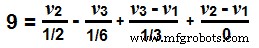
9 =2v ₂ + 6в ₃ + 3в ₃ – 3в ₁ + 0.

9 =– 3v ₁ + 2в ₂ + 9в ₃ …  → Уравнение 2.

Поскольку у нас есть три неизвестных значения, нам нужно еще одно уравнение. Незаметно, мы выберем источник напряжения 5В между узлами 2 и 3, т.е.

v ₂ – в ₃ =5  …  → Уравнение 3.

Решение уравнений 1, 2 и 3 с помощью правила Крамера или калькулятора правила Крамера , Устранение , Исключение Гаусса или компьютерная программа например, MATLAB , находим,

• в ₃ =0,575 В или 375 мВ.
• в ₂ =5,375 В.
• в ₁ =1,708 В.

Краткий обзор анализа суперузла (шаг за шагом)

1. Перерисуйте схему если можно.
2. Подсчитайте количество узлов в цепи.
3. Создание опорного узла . Это может быть узел с наибольшим количеством ветвей. Таким образом, мы можем минимизировать количество уравнений.
4. Назовите узловые напряжения . Какие (N-1) , где N – количество узлов.
5. Формировать надузел если цепь или сеть содержат источники напряжения. Эта работа выполняется путем закрытия терминала источника и другого элемента схемы, подключенного между двумя терминалами, корпусом, обозначенным пунктирной линией. Это показано на рис. 2 (b) выше.
6. Напишите KCL (Текущий закон Кирхгофа) для каждого нереференсного узла, а также для каждого суперузла, который не содержит эталонный узел. На первой стороне добавьте потоки, впадающие в суперузел. или узел из текущих источников. С другой стороны, добавьте токи, выходящие из суперузла или узла через резисторы. При записи уравнений KCL и решении схемы возьмите знак «-» в счете.
7. Для каждого определенного суперузла требуется один KCL (действующий закон Кирхгофа), что может быть достигнуто простым применением KCL . Проще говоря, свяжите напряжение на каждом источнике напряжения с узловыми напряжениями.
8. Если в цепи появляются зависимые источники , В этом случае укажите любые дополнительные неизвестные значения и такие величины, как токи или напряжения, отличные от узловых напряжений, с точки зрения подходящих узловых напряжений.
9. Расположите и организуйте систему уравнений .
10. Наконец, решите систему уравнений для узловых напряжений например, V₁ , В₂ и V₃ и т. д. их будет (N-1, где «N» =количество узлов). Если у вас возникли трудности с решением системы уравнений, обратитесь к приведенному выше примеру решения.

Похожие сообщения:

• Теорема Тевенина. Пошаговая процедура с решенным примером
• Теорема Нортона. Простая пошаговая процедура с примером (изображения)
• Закон Ома:простое объяснение с утверждением и формулами
• Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
• Закон Кирхгофа о токе и напряжении (KCL и KVL) | Решенный пример
• Теорема о компенсации – доказательство, объяснение и примеры решения
• Теорема о подстановке — пошаговое руководство с примером решения
• Теорема Миллмана. Анализ цепей переменного и постоянного тока. Примеры.
• Теорема о суперпозиции — анализ цепей с решенным примером
• Теорема Теллегена — Решенные примеры и моделирование в MATLAB
• Правило делителя напряжения (VDR) — примеры решений для цепей R, L и C
• Current Divider Rule (CDR) – Решенные примеры для цепей переменного и постоянного тока
• Преобразование из звезды в дельту и из дельты в звезду. Преобразование Y-Δ