Схема подключения

До сих пор мы анализировали схемы с одной батареей и одним резистором без учета соединительных проводов между компонентами, пока формируется полная цепь. Имеет ли значение для наших расчетов длина провода или «форма» цепи? Давайте посмотрим на несколько принципиальных схем и выясним:

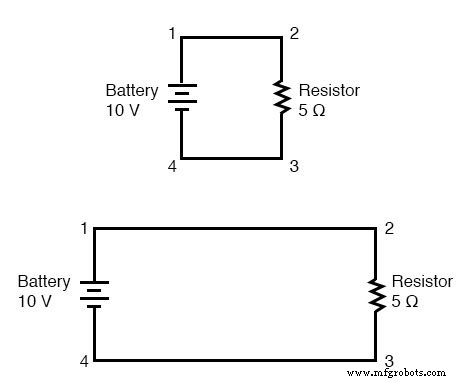
Когда мы рисуем провода, соединяющие точки в электрической цепи, мы обычно предполагаем, что эти провода имеют незначительное сопротивление. Как таковые, они не вносят заметного влияния на общее сопротивление цепи, и поэтому единственное сопротивление, с которым нам приходится бороться, - это сопротивление компонентов. В приведенных выше схемах единственное сопротивление исходит от резисторов 5 Ом, так что это все, что мы будем учитывать в наших расчетах.

В реальной жизни металлические проволоки действительно имеют сопротивление (как и источники питания!), но эти сопротивления обычно настолько меньше, чем сопротивление других компонентов схемы, что их можно безопасно игнорировать. Исключения из этого правила существуют в электропроводке энергосистемы, где даже очень небольшое сопротивление проводника может вызвать значительные падения напряжения при нормальных (высоких) уровнях тока.

Электрически общие точки в цепи

Если сопротивление соединительного провода очень мало или отсутствует, мы можем рассматривать соединенные точки в цепи как электрически общие . . То есть точки 1 и 2 в приведенных выше схемах могут быть физически соединены близко друг к другу или далеко друг от друга, и это не имеет значения для любых измерений напряжения или сопротивления относительно этих точек.

То же самое касается точек 3 и 4. Это как если бы концы резистора были присоединены непосредственно к клеммам батареи, что касается наших расчетов по закону Ома и измерений напряжения.

Это полезно знать, потому что это означает, что вы можете заново нарисовать принципиальную схему или повторно подключить схему, сокращая или удлиняя провода по желанию, не оказывая заметного влияния на работу схемы. Важно только то, что компоненты прикрепляются друг к другу в одинаковой последовательности.

Это также означает, что измерения напряжения между наборами «электрически общих» точек будут одинаковыми. То есть напряжение между точками 1 и 4 (непосредственно на батарее) будет таким же, как напряжение между точками 2 и 3 (непосредственно на резисторе). Внимательно посмотрите на следующую схему и попытайтесь определить, какие точки являются общими друг для друга:

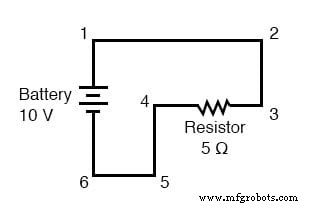
Здесь у нас есть только 2 компонента, не считая проводов:батарея и резистор. Хотя соединительные провода образуют законченную цепь извилистым путем, на пути тока есть несколько электрически общих точек. Точки 1, 2 и 3 являются общими друг для друга, потому что они напрямую связаны друг с другом проводом. То же самое и с пунктами 4, 5 и 6.

Напряжение между точками 1 и 6 составляет 10 вольт, идущее прямо от батареи. Однако, поскольку точки 5 и 4 являются общими для 6, а точки 2 и 3 являются общими для 1, те же 10 вольт также существуют между этими другими парами точек:

 Между точками 1 и 4 =10 вольт Между точками 2 и 4 =10 вольт Между точками 3 и 4 =10 вольт (непосредственно через резистор) Между точками 1 и 5 =10 вольт Между точками 2 и 5 =10 вольт Между точками 3 и 5 =10 В Между точками 1 и 6 =10 В (непосредственно на батарее) Между точками 2 и 6 =10 вольт Между точками 3 и 6 =10 вольт 

Поскольку электрически общие точки соединены вместе проводом (нулевого сопротивления), между ними нет значительного падения напряжения, независимо от величины тока, проводимого от одной к другой через этот соединительный провод. Таким образом, если бы мы считали напряжения между общими точками, мы должны были бы показать (практически) ноль:

 Между точками 1 и 2 =0 вольт Точки 1, 2 и 3 между точками 2 и 3 =0 В электрически общий Между точками 1 и 3 =0 вольт Между точками 4 и 5 =0 вольт Точки 4, 5 и 6 между точками 5 и 6 =0 В электрически общий Между точками 4 и 6 =0 вольт 

Расчет падения напряжения по закону Ома

Это тоже имеет смысл математически. С батареей на 10 В и резистором 5 Ом ток в цепи будет 2 ампера. Если сопротивление провода равно нулю, падение напряжения на любом непрерывном участке провода можно определить с помощью закона Ома как такового:

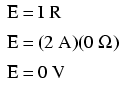
Должно быть очевидно, что рассчитанное падение напряжения на любом непрерывном отрезке провода в цепи, где предполагается, что провод имеет нулевое сопротивление, всегда будет равно нулю, независимо от величины тока, поскольку ноль, умноженный на что-либо, равен нулю.

Поскольку общие точки в цепи будут показывать одинаковые измерения относительного напряжения и сопротивления, провода, соединяющие общие точки, часто имеют одно и то же обозначение. Это не означает, что терминал точки подключения обозначены одинаково, только соединительные провода. Возьмем для примера эту схему:

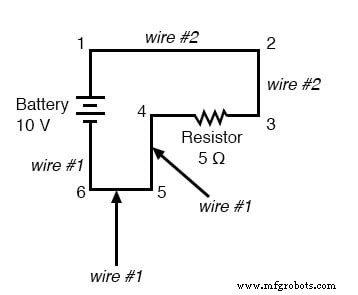
Точки 1, 2 и 3 являются общими друг для друга, поэтому точки подключения проводов 1–2 обозначены так же (провод 2), что и точки подключения проводов 2–3 (провод 2). В реальной схеме провод, тянущийся от точки 1 до 2, может даже не быть того же цвета или размера, что и провод, соединяющий точку 2 и 3, но они должны иметь точно такую ​​же метку. То же самое касается проводов, соединяющих точки 6, 5 и 4.

Падение напряжения должно равняться нулю в общих точках

Знание того, что электрически общие точки имеют нулевое падение напряжения, является ценным принципом поиска и устранения неисправностей. Если я измеряю напряжение между точками в цепи, которые должны быть общими друг для друга, я должен прочитать ноль.

Если, однако, я обнаружил значительное напряжение между этими двумя точками, то я с уверенностью знаю, что они не могут быть напрямую соединены друг с другом. Если эти баллы предполагаются чтобы быть электрически обычными, но они регистрируются иначе, тогда я знаю, что между этими точками есть «открытый сбой».

Нулевое напряжение технически означает незначительное напряжение

Последнее замечание:для большинства практических целей можно предположить, что проводники имеют нулевое сопротивление от конца до конца. В действительности, однако, всегда будет небольшое сопротивление по длине провода, если только это не сверхпроводящий провод. Зная это, мы должны помнить, что изученные здесь принципы, касающиеся общих электрических точек, в значительной степени действительны, но не для абсолютного степень.

То есть правило, согласно которому электрически общие точки гарантированно имеют нулевое напряжение между ними, более точно сформулировано как таковое:электрически общие точки будут иметь очень мало между ними упало напряжение. Этот небольшой, практически неизбежный след сопротивления, обнаруживаемый на любом участке соединительного провода, должен создавать небольшое напряжение по всей его длине, когда через него проходит ток.

Если вы понимаете, что эти правила основаны на идеальном условиях, вы не будете недоумевать, если столкнетесь с каким-либо условием, которое может оказаться исключением из правила.

ОБЗОР:

• Предполагается, что соединительные провода в цепи имеют нулевое сопротивление, если не указано иное.
• Провода в цепи можно укорачивать или удлинять, не влияя на работу схемы - все, что имеет значение, - это то, что компоненты подключены друг к другу в одной и той же последовательности.
• Точки, напрямую соединенные в цепь нулевым сопротивлением (проводом), считаются электрически общими . .
• Электрически общие точки с нулевым сопротивлением между ними будут иметь нулевое падение напряжения между ними, независимо от величины тока (в идеале).
• Показания напряжения или сопротивления между наборами электрически общих точек будут одинаковыми.
• Эти правила относятся к идеальному условия, при которых предполагается, что соединительные провода имеют абсолютно нулевое сопротивление. В реальной жизни это, вероятно, не так, но сопротивление проводов должно быть достаточно низким, чтобы общие принципы, изложенные здесь, по-прежнему действовали.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист простых схем
• Рабочий лист элементарной схемы
• Рабочий лист схемы делителя напряжения