Диаграммы и наборы Венна

Математики используют диаграммы Венна чтобы показать логические отношения наборов (коллекции объектов) друг к другу. Возможно, вы уже видели диаграммы Венна при изучении алгебры или других математических исследований. Если да, то вы можете вспомнить перекрывающиеся круги и объединение и пересечение наборов.

Мы рассмотрим перекрывающиеся круги диаграммы Венна. Мы будем использовать термины ИЛИ и И вместо объединения и пересечения, поскольку это терминология, используемая в цифровой электронике.

Диаграмма Венна соединяет булеву алгебру из предыдущей главы с картой Карно. Мы свяжем то, что вы уже знаете о булевой алгебре, с диаграммами Венна, а затем перейдем к картам Карно.

набор представляет собой набор объектов из юниверса, как показано ниже. участники набора - объекты, содержащиеся в наборе. У участников набора обычно есть что-то общее; однако это не является обязательным требованием.

Из вселенной действительных чисел, например, набор всех положительных целых чисел {1,2,3…} является набором. Набор {3,4,5} является примером меньшего набора или подмножества множества всех натуральных чисел. Другой пример - совокупность всех мужчин из вселенной студентов колледжа. Вы можете придумать еще несколько примеров наборов?

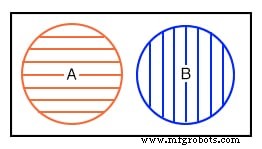
Вверху слева у нас есть диаграмма Венна, показывающая множество A в круге внутри вселенной U, прямоугольной области. Если все внутри круга - это A, то все, что находится за пределами круга, не является A. Таким образом, выше центра мы помечаем прямоугольную область за пределами круга A как A-not вместо U. Мы показываем B и B-not в a аналогичным образом.

Что произойдет, если и A, и B содержатся в одной вселенной? Мы показываем четыре возможности.

Давайте подробнее рассмотрим каждую из четырех возможностей, показанных выше.

Первый пример показывает, что набор A и набор B не имеют ничего общего согласно диаграмме Венна. Между областями A и B, заштрихованными круговыми штрихами, нет перекрытия. Например, предположим, что наборы A и B содержат следующие элементы:

 установить A ={1,2,3,4} установить B ={5,6,7,8} 

Ни один из элементов набора A не содержится в наборе B, ни один из элементов B не содержится в A. Таким образом, нет перекрытия кругов.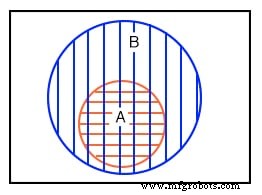

Во втором примере на приведенной выше диаграмме Венна набор A полностью содержится в наборе B. Как мы можем объяснить эту ситуацию? Предположим, что наборы A и B содержат следующие элементы:

 установить A ={1,2} установить B ={1,2,3,4,5,6,7,8} 

Все элементы набора A также являются членами набора B. Следовательно, набор A является подмножеством набора B. Поскольку все элементы набора A являются членами набора B, набор A полностью отрисовывается в границах набора B.

Есть пятый случай, который не показан, с четырьмя примерами. Подсказка:аналогично последнему (четвертому) примеру. Нарисуйте диаграмму Венна для пятого случая.

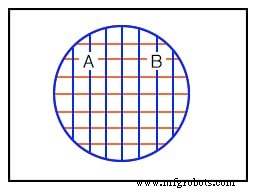
Третий пример выше показывает полное перекрытие между набором A и набором B. Похоже, что оба набора содержат одинаковые идентичные элементы. Предположим, что наборы A и B содержат следующее:

 установить A ={1,2,3,4} установить B ={1,2,3,4} 

Поэтому

 Установить A =Установить B 

Множества И B одинаково равны, потому что они оба имеют одинаковые идентичные элементы. Области A и B на соответствующей диаграмме Венна выше полностью перекрываются. Если есть какие-либо сомнения относительно того, что представляют собой вышеперечисленные шаблоны, обратитесь к любому рисунку выше или ниже, чтобы быть уверенным, как выглядели круглые области до того, как они были перекрыты.

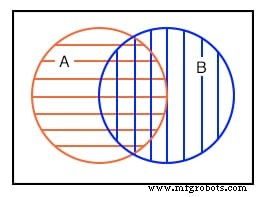
Четвертый пример выше показывает, что есть что-то общее между набором A и набором B в области перекрытия. Например, мы произвольно выбираем следующие наборы, чтобы проиллюстрировать нашу точку зрения:

 установить A ={1,2,3,4} установить B ={3,4,5,6} 

Оба набора A и B имеют общие элементы 3 и 4. Эти элементы являются причиной перекрытия центра, общего для A и B. Нам необходимо более внимательно изучить эту ситуацию.