Сложные схемы
Что мы будем делать, если встретим схему более сложную, чем простые последовательные конфигурации, которые мы видели до сих пор? Возьмем для примера эту схему:
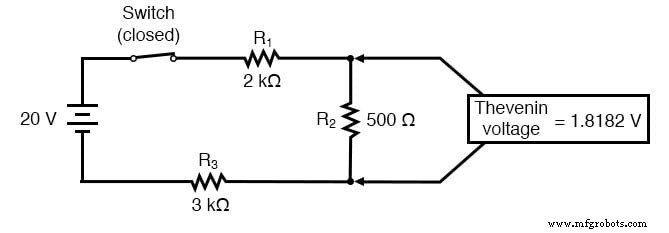
Простая формула постоянной времени (τ =RC) основана на простом последовательном сопротивлении, подключенном к конденсатору. В этом отношении формула постоянной времени для индуктивной цепи (τ =L / R) также основана на предположении о простом последовательном сопротивлении. Итак, что мы можем сделать в такой ситуации, когда резисторы соединены последовательно-параллельно с конденсатором (или катушкой индуктивности)?
Теорема Тевенина
Ответ дают наши исследования сетевого анализа. Теорема Тевенина говорит нам, что мы можем сократить любое преобразование линейной схемы в эквивалент одного источника напряжения, одного последовательного сопротивления и компонента нагрузки с помощью пары простых шагов. Чтобы применить теорему Тевенина к нашему сценарию здесь, мы будем рассматривать реактивную составляющую (в приведенном выше примере схемы, конденсатор) как нагрузку и временно отключать ее от схемы, чтобы найти напряжение Тевенина и сопротивление Тевенина.
Затем, как только мы определим значения эквивалентной схемы Тевенина, мы повторно подключим конденсатор и решим значения напряжения или тока с течением времени, как мы это делали до сих пор.
Определив конденсатор как «нагрузку», мы удаляем его из схемы и определяем напряжение на клеммах нагрузки (конечно, при условии, что переключатель замкнут):

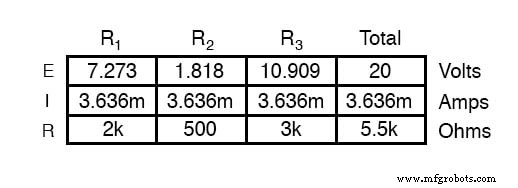
Этот шаг анализа показывает нам, что напряжение на клеммах нагрузки (такое же, как и на резисторе R 2 ) будет 1,8182 В без подключенной нагрузки. С небольшим отражением должно быть ясно, что это будет наше конечное напряжение на конденсаторе, поскольку полностью заряженный конденсатор действует как разомкнутая цепь, потребляя нулевой ток. Мы будем использовать это значение напряжения для напряжения источника нашей эквивалентной схемы Тевенина.
Теперь, чтобы вычислить сопротивление Тевенина, нам нужно исключить все источники питания в исходной цепи и рассчитать сопротивление, видимое с клемм нагрузки:
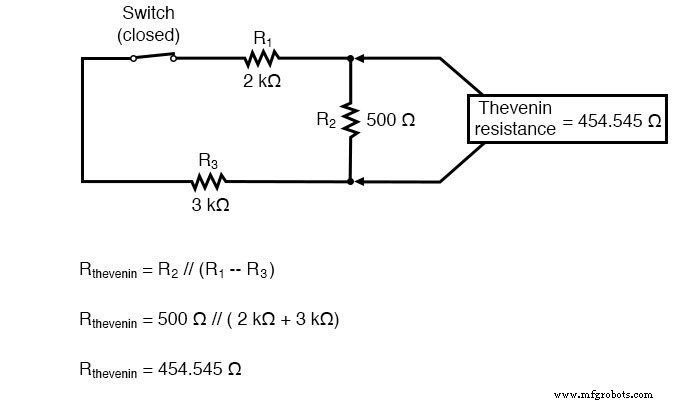
Перерисовывая нашу схему как эквивалент Тевенина, мы получаем следующее:
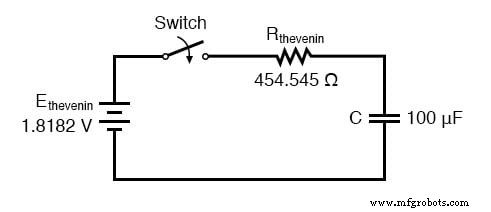
Наша постоянная времени для этой цепи будет равна сопротивлению Тевенина, умноженному на емкость (τ =RC). Используя указанные выше значения, мы рассчитываем:

Теперь мы можем найти напряжение на конденсаторе напрямую с помощью нашей универсальной формулы постоянной времени. Давайте посчитаем значение 60 миллисекунд. Поскольку это емкостная формула, мы настроим наши расчеты для напряжения:

Опять же, поскольку наше начальное значение напряжения конденсатора было принято равным нулю, фактическое напряжение на конденсаторе за 60 миллисекунд равно величине изменения напряжения от нуля, или 1,3325 вольт.
Мы могли бы пойти еще дальше и продемонстрировать эквивалентность RC-цепи Тевенина и исходной схемы с помощью компьютерного анализа. Я буду использовать программу анализа SPICE, чтобы продемонстрировать это:
Сравнительный RC-анализ * сначала список соединений для исходной схемы:v1 1 0 постоянного тока 20 г1 1 2 2к г2 2 3 500 r3 3 0 3k c1 2 3 100u ic =0 * тогда список соединений для эквивалента thevenin:v2 4 0 постоянного тока 1.818182 г4 4 5 454,545 c2 5 0100u ic =0 * теперь мы анализируем переходный процесс, выборка каждые 0,005 секунды * в течение всего 0,37 секунды, распечатывая список * значения напряжения на конденсаторе в оригинале * цепь (между режимами 2 и 3) и через конденсатор в * эквивалентная схема Тевенина (между узлами 5 и 0) .tran .005 0,37 мкК .print tran v (2,3) v (5,0) .конец
Что печатается как:
На каждом этапе анализа конденсаторы в двух схемах (исходная схема и эквивалентная схема Тевенина) находятся под одинаковым напряжением, что демонстрирует эквивалентность двух схем.
ОБЗОР:
- Чтобы проанализировать RC- или L / R-схему, более сложную, чем простая последовательная, преобразуйте схему в эквивалент Тевенина, рассматривая реактивный компонент (конденсатор или катушку индуктивности) как «нагрузку» и уменьшив все остальное до эквивалентной схемы одного источник напряжения и один последовательный резистор. Затем проанализируйте, что происходит с течением времени, с помощью формулы универсальной постоянной времени.
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:
- Рабочий лист теорем Тевенина, Нортона и максимальной мощности
Промышленные технологии
- Уравнения цепи переменного тока
- Цепи управления двигателем
- Использование нескольких комбинационных схем
- Схемы усилителя
- Радиосхемы
- Цепи управления
- Что такое электрические цепи?
- Компьютерное моделирование электрических цепей
- Резонанс в последовательно-параллельных цепях
- Введение в различные гидравлические схемы



