Вычислительные схемы

Когда кто-то упоминает слово «компьютер», обычно на ум приходит цифровое устройство. Цифровые схемы представляют числовые величины в двоичном формате формат:комбинации единиц и нулей, представленные множеством транзисторных схем, работающих в насыщенном или отсеченном состояниях. Однако аналоговая схема также может использоваться для представления числовых величин и выполнения математических расчетов с использованием сигналов переменного напряжения вместо дискретных состояний включения / выключения.

Вот простой пример двоичного (цифрового) представления в сравнении с аналоговым представлением числа «двадцать пять»:

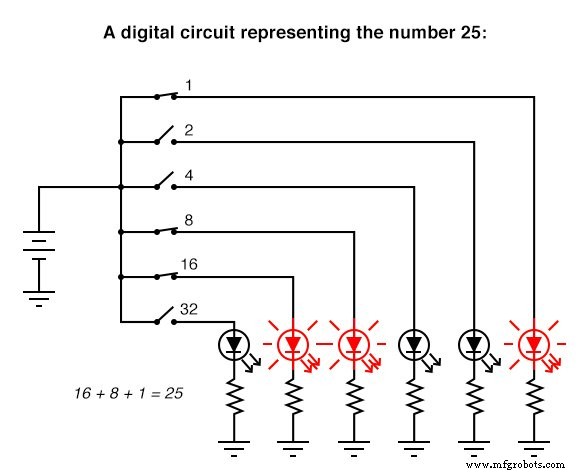
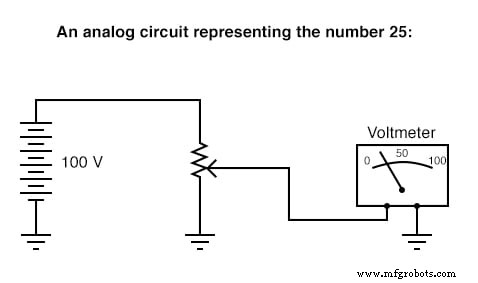
Цифровые схемы сильно отличаются от схем, построенных на аналоговых принципах. Цифровые вычислительные схемы могут быть невероятно сложными, и для получения окончательного ответа расчеты часто должны выполняться в виде последовательных «шагов», подобно тому, как человек может выполнять арифметические вычисления поэтапно с помощью карандаша и бумаги. С другой стороны, аналоговые вычислительные схемы довольно просты в сравнении и выполняют свои вычисления непрерывно в режиме реального времени. Однако есть недостаток использования аналоговой схемы для представления чисел:неточность. Цифровая схема, показанная выше, точно представляет число двадцать пять. Показанная выше аналоговая схема может или не может быть точно откалибрована на 25 000 вольт, но подвержена «дрейфу» и ошибкам.

В приложениях, где точность не критична, аналоговые вычислительные схемы очень практичны и элегантны. Здесь показаны несколько схем операционного усилителя для выполнения аналоговых вычислений:

Вычислительные схемы операционных усилителей

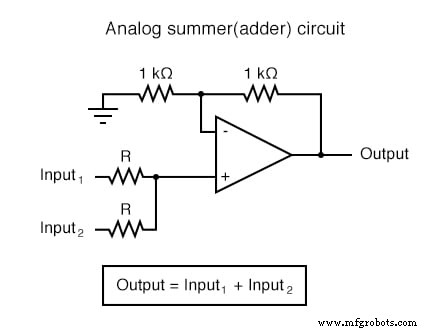
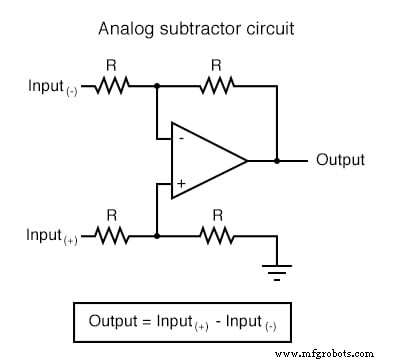
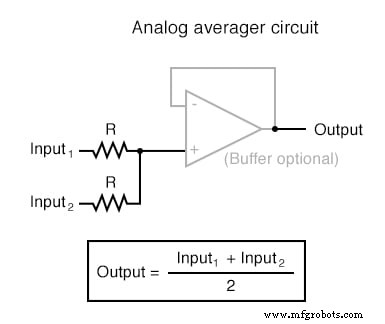
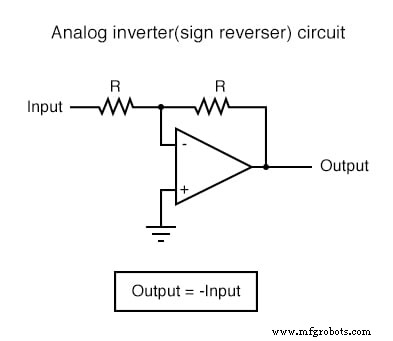
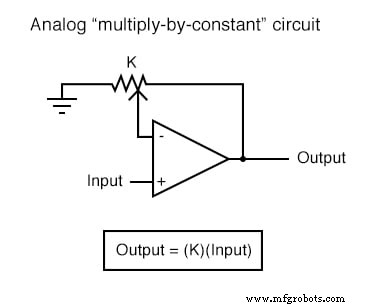
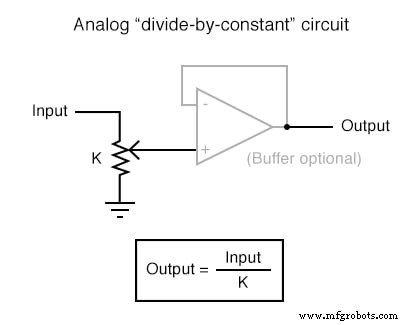
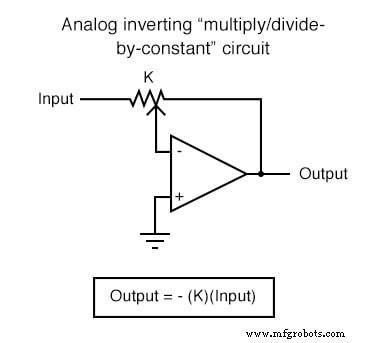
Каждую из этих схем можно использовать по модульному принципу для создания схемы, способной выполнять несколько вычислений. Например, предположим, что нам нужно вычесть определенную долю одной переменной из другой переменной. Объединив схему деления на константу со схемой вычитания, мы могли бы получить требуемую функцию:

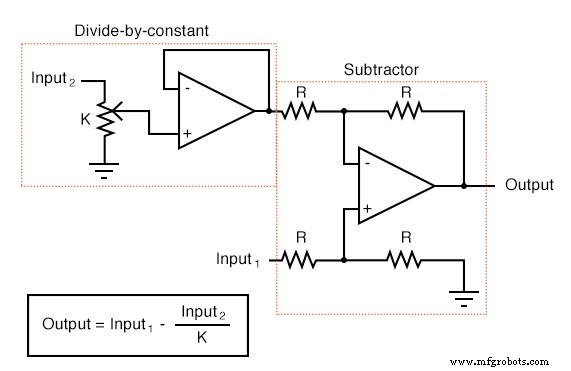
Устройства, называемые аналоговыми компьютерами раньше было обычным явлением в университетах и ​​инженерных мастерских, где десятки схем операционных усилителей могли быть «соединены» вместе со съемными перемычками для моделирования математических утверждений, обычно с целью моделирования какого-либо физического процесса, лежащие в основе уравнения которого были известны. Цифровые компьютеры сделали аналоговые компьютеры почти устаревшими, но аналоговые вычислительные схемы не могут быть побеждены цифровыми с точки зрения чистой элегантности и экономии необходимых компонентов.

Аналоговая вычислительная схема отлично справляется с вычислительными операциями интегрированием и дифференциация относительно времени за счет использования конденсаторов в цепи обратной связи операционного усилителя. Однако, чтобы полностью понять работу и приложения этих схем, мы должны сначала понять значение этих фундаментальных концепций исчисления. К счастью, применение схем операционного усилителя к реальным задачам, связанным с исчислением, служит отличным средством обучения основам исчисления. По словам Джона И. Смита из его выдающегося учебника Modern Operational Circuit Design :

«Некоторым читателям предлагается примечание ободрения:интегральное исчисление - одна из математических дисциплин, которые используются в схемах операционных [усилителей] и при этом скорее разрушают как препятствие для понимания». (стр. 4)

Мнения г-на Смита о педагогической ценности аналоговых схем как учебного пособия по математике не уникальны. Примите во внимание мнение инженера Джорджа Фокса Лэнга в статье, которую он написал для августовского выпуска журнала Sound and Vibration за 2000 год. , озаглавленный:«Аналог был не компьютерная торговая марка! »:

«Создание реальной физической сущности (схемы), управляемой определенным набором уравнений, и взаимодействие с ней обеспечивает уникальное понимание этих математических утверждений. Нет лучшего способа развить «чутье» на взаимодействие между физикой и математикой, чем испытать такое взаимодействие. Аналоговый компьютер был мощным междисциплинарным обучающим инструментом; его устаревание оплакивают многие преподаватели в самых разных областях ». (стр. 23)

Дифференциация - это первая операция, которую обычно изучают начинающие студенты, изучающие математику. Проще говоря, дифференциация определяет мгновенную скорость изменения одной переменной по отношению к другой. В схемах аналогового дифференциатора независимой переменной является время, поэтому скорости изменения, с которыми мы имеем дело, представляют собой скорости изменения электронного сигнала (напряжения или тока) относительно времени.

Предположим, мы должны были измерить положение автомобиля, движущегося по прямому пути (без поворотов), от начальной точки. Назовем это измерение x . Если автомобиль движется с такой скоростью, что расстояние от «старта» до него неуклонно увеличивается с течением времени, его положение будет отображаться на графике в виде линейного функция (прямая линия):

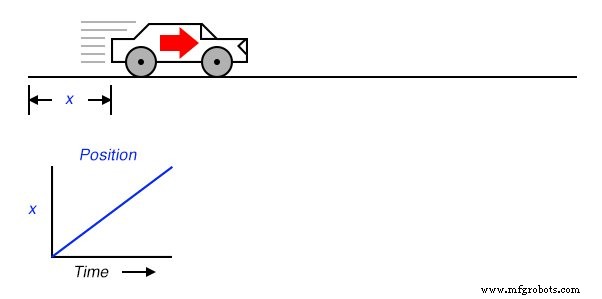
Если бы мы вычислили производную положения автомобиля относительно времени (то есть определить скорость изменения положения автомобиля относительно времени), мы пришли бы к величине, представляющей скорость автомобиля. Функция дифференцирования представлена ​​дробным обозначением d / d . , поэтому при различении позиции ( x ) по времени ( t ), мы обозначим результат (производную) как dx / dt :

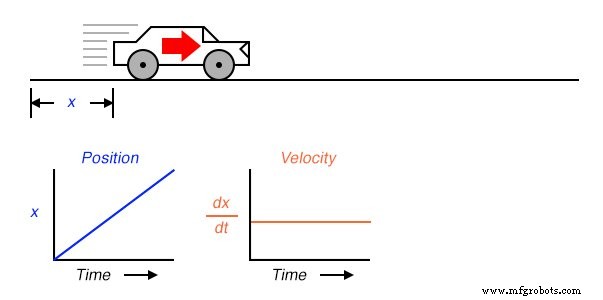
Для линейного графика x со временем производное от позиции ( dx / dt ), иначе и более известное как скорость , будет ровной линией, неизменной по значению. Графически производная математической функции может пониматься как ее наклон при нанесении на график, и здесь мы видим, что позиция ( x ) график имеет постоянный наклон, что означает, что его производная ( dx / dt ) должен быть постоянным во времени.

Теперь предположим, что расстояние, пройденное автомобилем, экспоненциально увеличивалось с течением времени:то есть он начал свой путь медленными движениями, но преодолел все большее дополнительное расстояние с каждым периодом времени. Тогда мы увидим, что производная от позиции ( dx / dt ), иначе известная как скорость ( v ), не будет постоянным с течением времени, но будет увеличиваться:

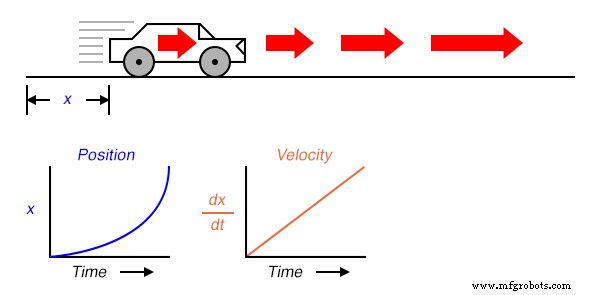
Высота точек на графике скорости соответствует скорости изменения или наклону точек в соответствующие моменты времени на графике положения:

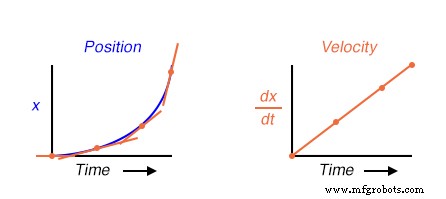
При чем здесь аналоговые электронные схемы? Что ж, если бы у нас был аналоговый сигнал напряжения, представляющий положение автомобиля (представьте себе огромный потенциометр, стеклоочиститель которого был прикреплен к автомобилю, генерирующий напряжение, пропорциональное положению автомобиля), мы могли бы подключить схему дифференциатора к этому сигналу и получить схема непрерывно вычислить скорость автомобиля с отображением результата через вольтметр, подключенный к выходу схемы дифференциатора:

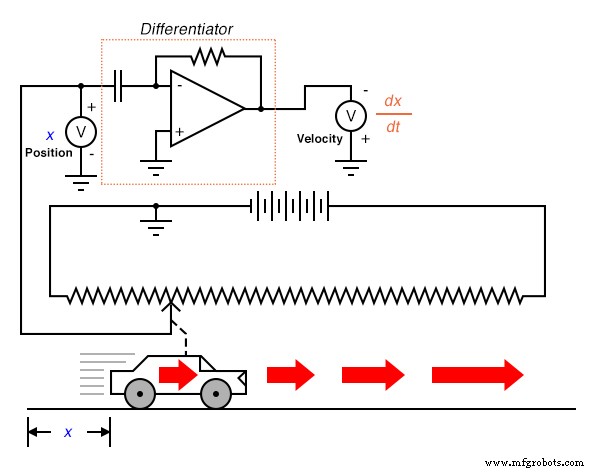
Вспомните из предыдущей главы, что схема дифференциатора выдает напряжение, пропорциональное скорости изменения входного напряжения во времени . ( d / dt ). Таким образом, если входное напряжение изменяется со временем с постоянной скоростью , выходное напряжение будет постоянным. Если автомобиль движется таким образом, что пройденное расстояние с течением времени увеличивается с постоянной скоростью, это означает, что автомобиль движется с постоянной скоростью, и схема дифференциатора будет выдавать постоянное напряжение, пропорциональное этой скорости. Если пройденное расстояние автомобиля с течением времени изменяется нестационарно, выходной сигнал схемы дифференциатора также будет нестабильным, но всегда на уровне, представляющем скорость изменения входного сигнала с течением времени.

Отметим, что вольтметр, регистрирующий скорость (на выходе схемы дифференциатора), подключен с «обратной» полярностью к выходу операционного усилителя. Это потому, что показанная схема дифференциатора инвертирующая :вывод отрицательного напряжения для положительной скорости изменения входного напряжения. Если мы хотим, чтобы вольтметр регистрировал положительное значение скорости, его необходимо подключить к операционному усилителю, как показано. Каким бы непрактичным ни было подключение гигантского потенциометра к движущемуся объекту, например, автомобилю, концепция должна быть ясной:выполняя электронное вычисление функции дифференцирования для сигнала, представляющего положение, мы получаем сигнал, представляющий скорость.

Начинающие студенты-математики изучают символические методы дифференциации. Однако для этого необходимо знать уравнение, описывающее исходный график. Например, студенты, изучающие математику, узнают, как взять такую ​​функцию, как y =3x и найти его производную по x ( d / dx ), 3 , просто манипулируя уравнением. Мы можем проверить точность этой манипуляции, сравнив графики двух функций:

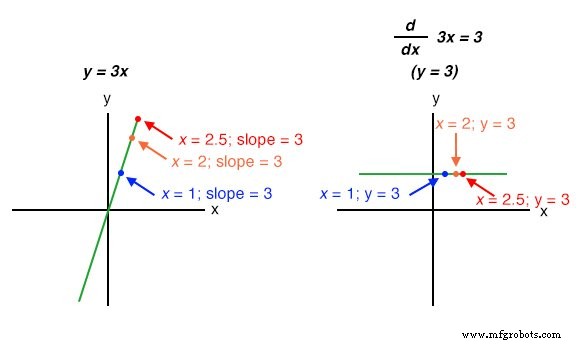
Нелинейные функции, такие как y =3x ² также могут различаться символическими средствами. В этом случае производная от y =3x ² относительно x 6x :

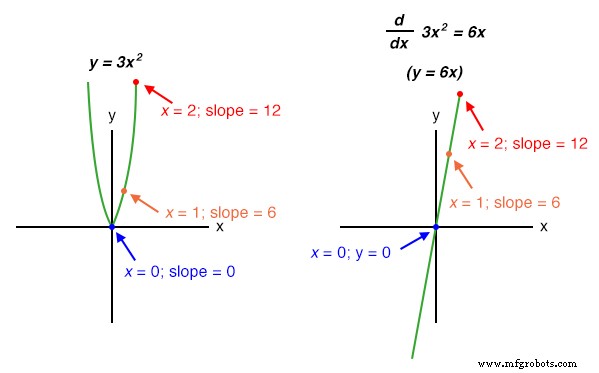
Однако в реальной жизни мы часто не можем описать поведение какого-либо физического события простым уравнением типа y =3x . , и поэтому символическая дифференциация того типа, который усвоили изучающие математику, может быть невозможно применить к физическому измерению. Если кто-то хотел определить производную от положения нашего гипотетического автомобиля ( dx / dt =скорость) символическими средствами, они сначала должны были бы получить уравнение, описывающее положение автомобиля во времени, основанное на измерениях положения, сделанных в реальном эксперименте - почти невыполнимая задача, если только автомобиль не эксплуатируется в тщательно контролируемых условиях, приводящих к очень простой граф положения. Однако аналоговая схема дифференциатора, использующая поведение конденсатора в отношении напряжения, тока и времени i =C (dv / dt) , естественно дифференцирует любой реальный сигнал по времени и может выводить сигнал, соответствующий мгновенной скорости ( dx / dt ) в любой момент. Регистрируя сигнал положения автомобиля вместе с выходным сигналом дифференциатора с помощью самописца или другого устройства сбора данных, оба графика естественным образом представляются для проверки и анализа.

Мы можем пойти дальше принципа дифференцирования, применив его к сигналу скорости с помощью другой схемы дифференцирования. Другими словами, используйте его для расчета скорости изменения скорости, которая, как мы знаем, является скоростью изменения положения. К какой практической мере мы пришли бы, если бы сделали это? Подумайте об этом с точки зрения единиц измерения, которые мы используем для измерения положения и скорости. Если бы мы измеряли положение автомобиля от начальной точки в милях, то, вероятно, выражали бы его скорость в милях в час . ( dx / dt ). Если бы мы продифференцировали скорость (измеренную в милях в час) по времени, мы получили бы единицу измерения миль в час в час . На вводных курсах физики учащимся рассказывается о поведении падающих предметов и измерении положения в метрах . , скорость в метрах в секунду , и изменение скорости с течением времени в метрах в секунду, в секунду . Эта последняя мера называется ускорением . :скорость изменения скорости во времени:

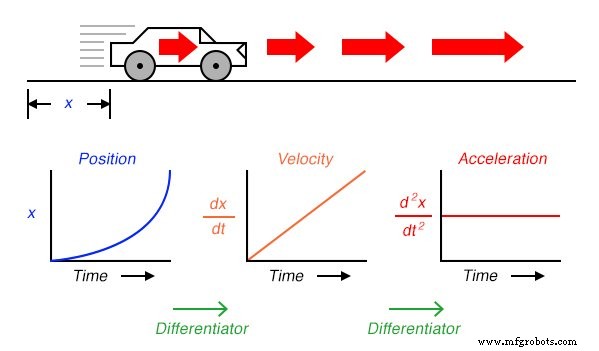
Выражение d ² x / dt ² называется второй производной позиции ( x ) по времени ( t ). Если бы мы подключили вторую схему дифференциатора к выходу первого, последний вольтметр регистрировал бы ускорение:

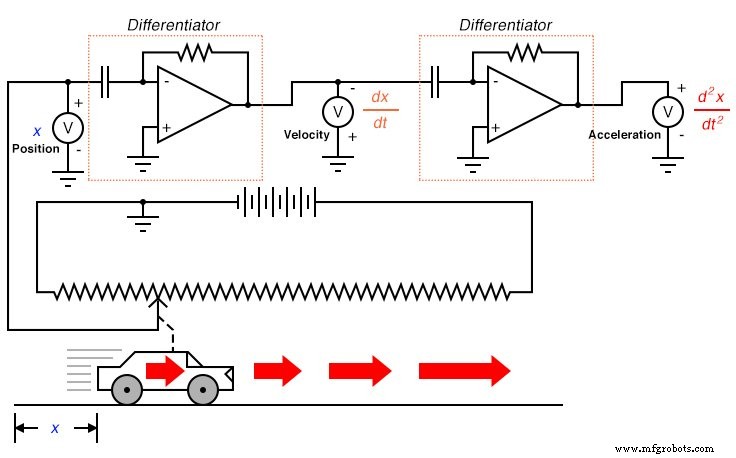
Получая скорость из положения и ускорение из скорости, мы видим, как очень четко проиллюстрирован принцип дифференциации. Это не единственные физические измерения, связанные друг с другом таким образом, но они, пожалуй, самые распространенные. Другой пример действующего исчисления - взаимосвязь между потоком жидкости ( q ) и жидкого объема ( v ) накапливается в сосуде с течением времени:

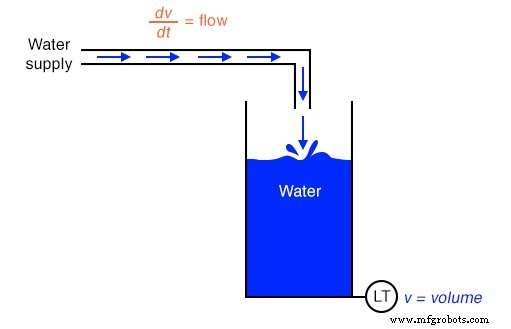
Устройство «Датчик уровня», установленное на резервуаре для хранения воды, выдает сигнал, прямо пропорциональный уровню воды в резервуаре, который - если резервуар имеет постоянную площадь поперечного сечения по всей его высоте - прямо соответствует хранящемуся объему воды. Если бы мы взяли этот объемный сигнал и дифференцировали его по времени ( dv / dt ), мы получили бы сигнал, пропорциональный расходу воды расходом через трубу, по которой вода поступает в резервуар. Схема дифференциатора, подключенная таким образом, чтобы принимать этот объемный сигнал, будет производить выходной сигнал, пропорциональный потоку, возможно, заменяя устройство измерения потока («Датчик потока»), установленное в трубе.

Возвращаясь к автомобильному эксперименту, предположим, что наша гипотетическая машина была оборудована тахогенератором на одном из колес, производящим сигнал напряжения, прямо пропорциональный скорости. Мы могли бы дифференцировать сигнал, чтобы получить ускорение с помощью одной схемы, например:

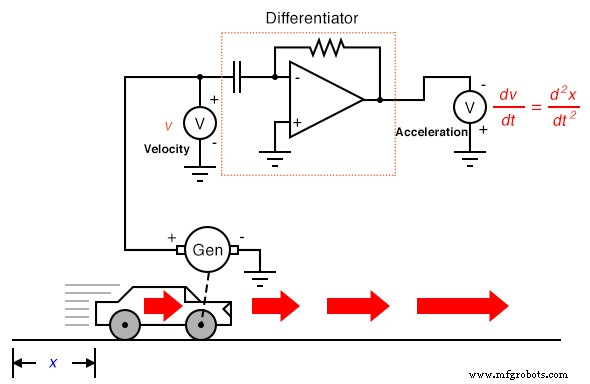
По самой своей природе тахогенератор определяет положение автомобиля во времени, генерируя напряжение, пропорциональное тому, насколько быстро угловое положение колеса изменяется с течением времени. Это дает нам необработанный сигнал, уже представляющий скорость, с единственным шагом дифференцирования, необходимым для получения сигнала ускорения. Тахогенератор, измеряющий скорость, конечно же, является гораздо более практичным примером автомобильной аппаратуры, чем гигантский потенциометр, измеряющий его физическое положение, но то, что мы получаем с практической точки зрения, мы теряем при измерении положения. Независимо от того, сколько раз мы проводим различие, мы никогда не сможем определить положение автомобиля по сигналу скорости. Если процесс дифференциации привел нас от положения к скорости к ускорению, тогда нам нужно каким-то образом выполнить «обратный» процесс дифференцирования, чтобы перейти от скорости к положению. Такой математический процесс действительно существует, и он называется интегрированием . . Схема «интегратора» может использоваться для выполнения этой функции интегрирования по времени:

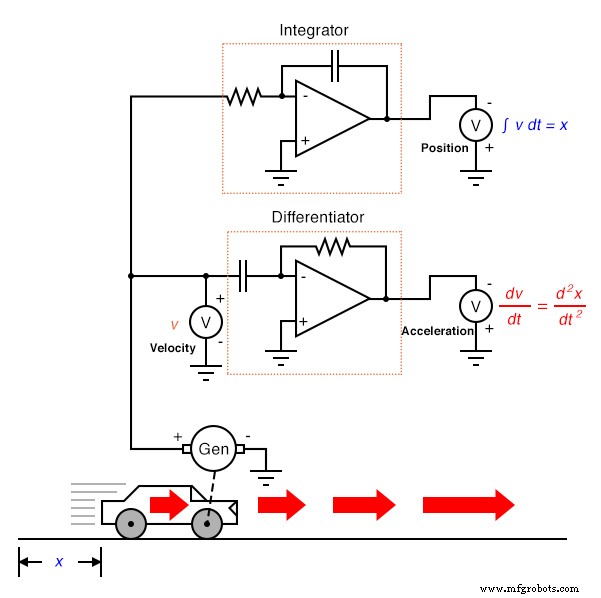
Вспомните из предыдущей главы, что схема интегратора выдает напряжение, скорость изменения которого во времени пропорциональна величине входного напряжения. Таким образом, при постоянном входном напряжении выходное напряжение будет изменяться . с постоянной скоростью . Если автомобиль движется с постоянной скоростью (постоянное напряжение, поступающее в схему интегратора от тахогенератора), то пройденное расстояние будет неуклонно увеличиваться с течением времени, и интегратор будет выдавать постоянно изменяющееся напряжение, пропорциональное этому расстоянию. Если скорость автомобиля непостоянна, то скорость изменения во времени не будет зависеть от выходного сигнала схемы интегратора, но выходное напряжение будет точно отображать расстояние, пройденное автомобилем в любой момент времени.

Символ интеграции выглядит как очень узкая курсивная буква «S» (∫). Уравнение, использующее этот символ (∫ v dt =x ) сообщает нам, что мы интегрируем скорость ( v ) по времени ( dt ) и получение позиции ( x ) в результате.

Итак, мы можем выразить три показателя движения автомобиля (положение, скорость и ускорение) через скорость ( v ) так же легко, как и с точки зрения позиции ( x ):

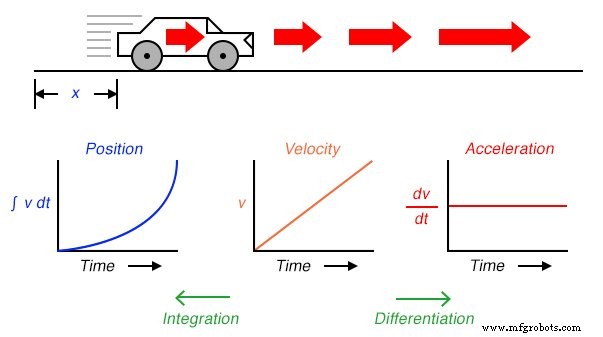
Если бы у нас был акселерометр, прикрепленный к автомобилю, генерирующий сигнал, пропорциональный скорости ускорения или замедления, мы могли бы (гипотетически) получить сигнал скорости с одним шагом интегрирования и сигнал положения со вторым шагом интегрирования:

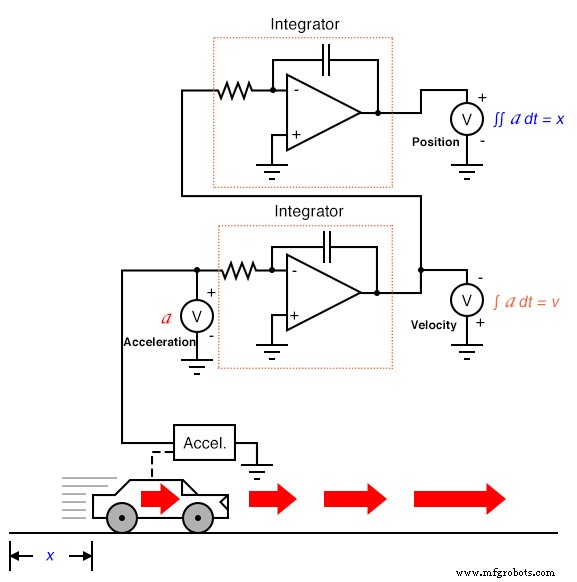
Таким образом, все три показателя движения автомобиля (положение, скорость и ускорение) могут быть выражены в терминах ускорения:

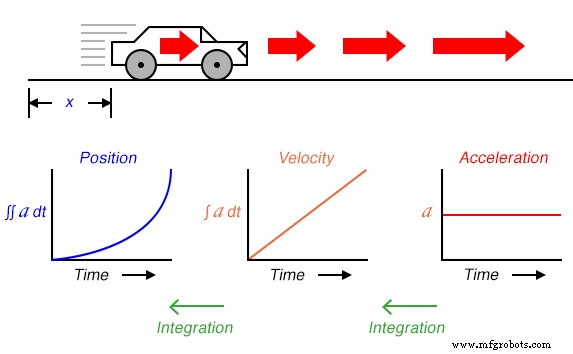
Как вы могли догадаться, процесс интеграции можно проиллюстрировать и применить к другим физическим системам. Возьмем, к примеру, резервуар для воды и пример потока, показанные ранее. Если скорость потока является производной объема резервуара по времени ( q =dv / dt ), то можно также сказать, что объем - это интеграл расхода по времени:

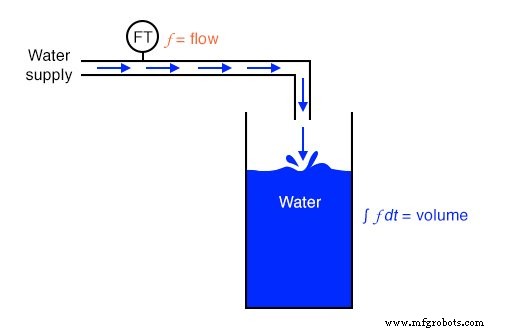
Если бы мы использовали устройство «Датчик расхода» для измерения расхода воды, то с помощью интегрирования по времени мы могли бы вычислить объем воды, накопленный в резервуаре с течением времени. Хотя теоретически возможно использовать схему интегратора емкостного операционного усилителя для получения объемного сигнала из сигнала потока, механические и цифровые электронные «интеграторы» более подходят для интеграции в течение длительных периодов времени и часто используются в воде. отрасли обработки и распределения.

Так же, как существуют символические методы дифференциации, существуют также символические методы интеграции, хотя они, как правило, более сложные и разнообразные. Однако применение символьной интеграции к реальной проблеме, такой как ускорение автомобиля, по-прежнему зависит от наличия уравнения, точно описывающего измеряемый сигнал - часто трудно или невозможно вывести из измеренных данных. Однако схемы электронного интегратора выполняют эту математическую функцию непрерывно, в реальном времени и для любых профиль входного сигнала, предоставляя тем самым мощный инструмент для ученых и инженеров.

Сказав это, есть предостережения в отношении использования методов исчисления для получения одного типа измерения из другого. Дифференциация имеет нежелательную тенденцию к усилению «шума», обнаруживаемого в измеряемой переменной, поскольку шум обычно проявляется в виде частот, намного превышающих измеряемую переменную, а высокие частоты по самой своей природе обладают высокой скоростью изменения во времени.

Чтобы проиллюстрировать эту проблему, предположим, что мы производим измерение ускорения автомобиля по сигналу скорости, полученному от тахогенератора с изношенными щетками или переключающими стержнями. Точки плохого контакта между щеткой и коммутатором будут вызывать кратковременные «провалы» выходного напряжения тахогенератора, и подключенная к нему схема дифференциатора будет интерпретировать эти провалы как очень быстрые изменения скорости. Для автомобиля, движущегося с постоянной скоростью - без ускорения или замедления - сигнал ускорения должен составлять 0 вольт, но «шум» в сигнале скорости, вызванный неисправным тахогенератором, приведет к тому, что дифференцированный сигнал (ускорение) будет содержать «пики», что ложно указывает на короткие периоды резкого ускорения и замедления:

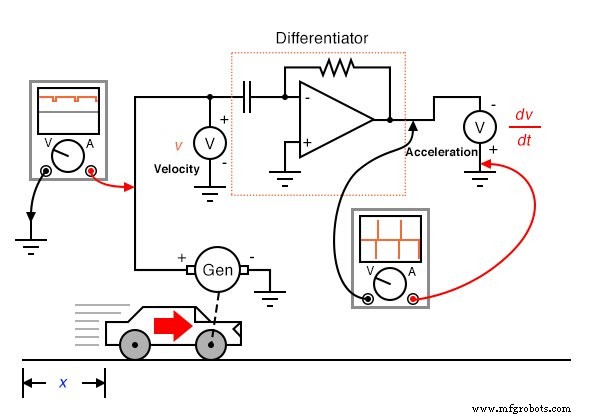
Шумовое напряжение, присутствующее в дифференцируемом сигнале, не обязательно должно иметь значительную амплитуду, чтобы вызвать проблемы:все, что требуется, - это чтобы профиль шума имел быстрое время нарастания или спада. Другими словами, любой электрический шум с высоким значением dv / dt компонент будет проблематичным при дифференцировании, даже если он имеет низкую амплитуду.

Следует отметить, что эта проблема не является артефактом (идиосинкразической ошибкой измерительного / вычислительного прибора) аналоговой схемы; скорее, это присуще процессу дифференциации. Независимо от того, как мы можем выполнять дифференцирование, «шум» в сигнале скорости неизменно искажает выходной сигнал. Конечно, если мы дифференцируем сигнал дважды, как мы это делали для получения скорости и ускорения из сигнала положения, усиленный шумовой сигнал, выводимый первой схемой дифференциатора, будет снова усилен следующим дифференциатором, что усугубит проблему:

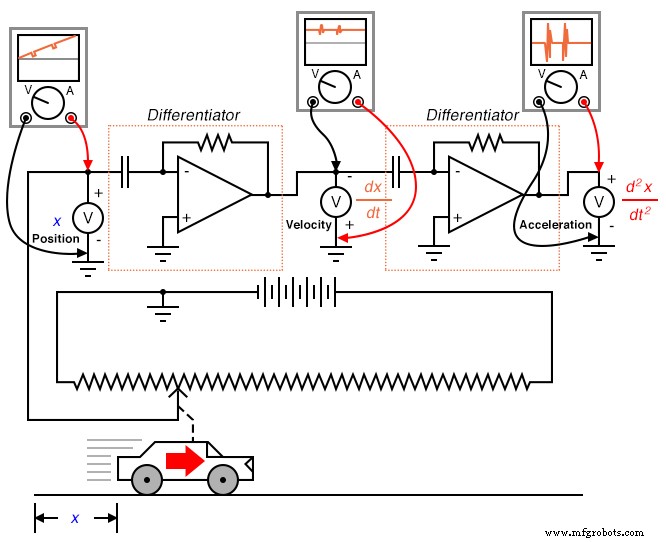
Интеграция не страдает от этой проблемы, потому что интеграторы действуют как фильтры нижних частот, ослабляя высокочастотные входные сигналы. Фактически, все высокие и низкие пики, возникающие из-за шума в сигнале, усредняются вместе с течением времени, что приводит к уменьшению конечного результата. Тогда можно было бы предположить, что мы могли бы избежать всех проблем, если бы напрямую измерили ускорение и интегрировали этот сигнал для получения скорости; фактически, вычисление «в обратном» порядке, как было показано ранее:

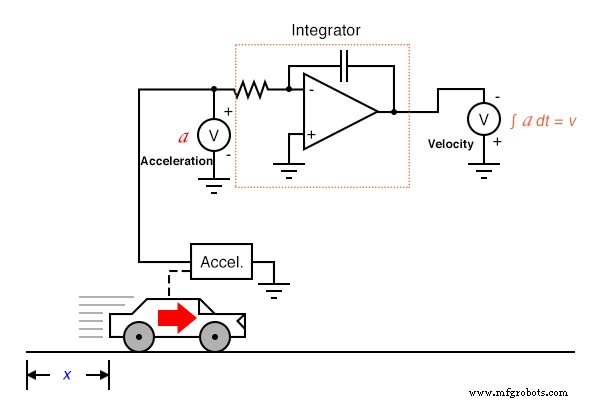
К сожалению, следование этой методике может привести нас к другим трудностям, одна из которых является обычным артефактом схем аналогового интегратора, известным как дрейф . . Все операционные усилители имеют некоторое количество входного тока смещения, и этот ток будет иметь тенденцию вызывать накопление заряда на конденсаторе в дополнение к тому заряду, который накапливается в результате сигнала входного напряжения. Другими словами, все схемы аналогового интегратора страдают от тенденции иметь выходное напряжение «дрейфа» или «ползучести» даже при полном отсутствии входного напряжения, в результате чего со временем накапливаются ошибки. Кроме того, несовершенные конденсаторы со временем будут терять свой накопленный заряд из-за внутреннего сопротивления, что приводит к «дрейфу» в сторону нулевого выходного напряжения. Эти проблемы являются артефакты аналоговой схемы и могут быть устранены с помощью цифровых вычислений.

Несмотря на артефакты схемы, возможные ошибки могут возникнуть в результате интеграции одного измерения (например, ускорения) для получения другого (например, скорости) просто из-за того, как работает интеграция. Если «нулевая» точка калибровки датчика необработанного сигнала не идеальна, он будет выдавать небольшой положительный или отрицательный сигнал даже в условиях, когда он ничего не должен выдавать. Рассмотрим автомобиль с неправильно откалиброванным акселерометром или тот, на который действует сила тяжести, чтобы обнаружить небольшое ускорение, не связанное с движением автомобиля. Даже при идеальном интегрирующем компьютере эта ошибка датчика заставит интегратор накапливать ошибку, что приводит к выходному сигналу, указывающему на изменение скорости, когда автомобиль не ускоряется и не замедляется.

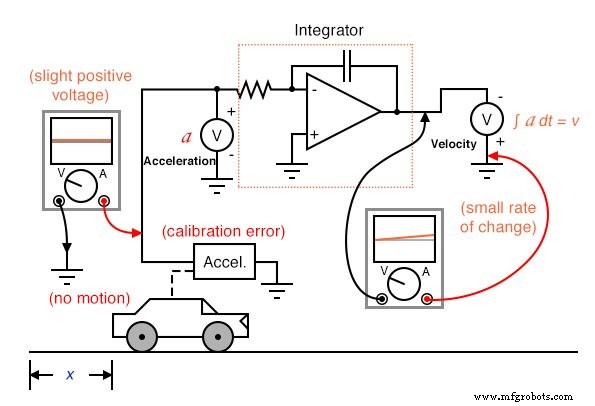
Как и в случае дифференцирования, эта ошибка также усугубится, если интегрированный сигнал будет передан в другую схему интегратора, поскольку «дрейфующий» выход первого интегратора очень скоро представит значительный положительный или отрицательный сигнал для следующего интегратора для интегрирования. Следовательно, следует соблюдать осторожность при объединении сигналов датчика:если установка датчика на «ноль» не идеальная , интегрированный результат будет дрейфовать, даже если сама схема интегратора идеальна.

Пока что единственные обсуждаемые ошибки интеграции носили искусственный характер:они возникают из-за недостатков в схемах и датчиках. Также существует источник ошибки, присущий самому процессу интеграции, и это неизвестная константа . проблема. Начинающие студенты-математики узнают, что всякий раз, когда функция интегрируется, существует неизвестная константа (обычно представленная как переменная C ) добавлен к результату. Эту неопределенность легче всего понять, сравнив производные нескольких функций, которые отличаются только добавлением постоянного значения:

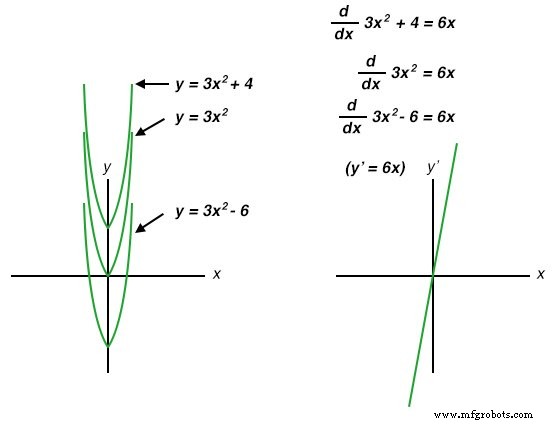
Обратите внимание на то, как каждая параболическая кривая ( y =3x ² + C ) имеют одинаковую форму, но отличаются друг от друга вертикальным смещением. Однако все они имеют одну и ту же производную функцию: y ’=(d / dx) (3x ² + C) =6x , потому что все они имеют одинаковую скорость изменения (наклоны) в соответствующих точках вдоль x ось. Хотя это кажется вполне естественным и ожидаемым с точки зрения дифференциации (разные уравнения имеют общую производную), это обычно кажется начинающим студентам странным с точки зрения интеграции, потому что существует несколько правильных ответов для интеграла функции. Переходя от уравнения к его производной, есть только один ответ, но переход от этой производной к исходному уравнению приводит нас к ряду правильных решений. В честь этой неопределенности символическая функция интегрирования называется неопределенным интегралом . .

Когда интегратор выполняет интегрирование живого сигнала по времени, выходной сигнал представляет собой сумму интегрированного входного сигнала по времени и начальное значение произвольной величины, представляющее ранее существовавший выходной сигнал интегратора на момент начала интегрирования. Например, если я проинтегрирую скорость автомобиля, едущего по прямой от города, вычислив, что постоянная скорость 50 миль в час в течение 2 часов даст расстояние (∫ v dt ) 100 миль, это не обязательно означает, что автомобиль будет в 100 милях от города через 2 часа. Все, что он нам говорит, это то, что машина будет на 100 миль дальше подальше от города через 2 часа езды. Фактическое расстояние от города после 2 часов езды зависит от того, как далеко находился автомобиль от города в момент начала интеграции. Если мы не знаем это начальное значение расстояния, мы не сможем определить точное расстояние автомобиля от города через 2 часа езды.

Эта же проблема возникает, когда мы интегрируем ускорение по времени, чтобы получить скорость:

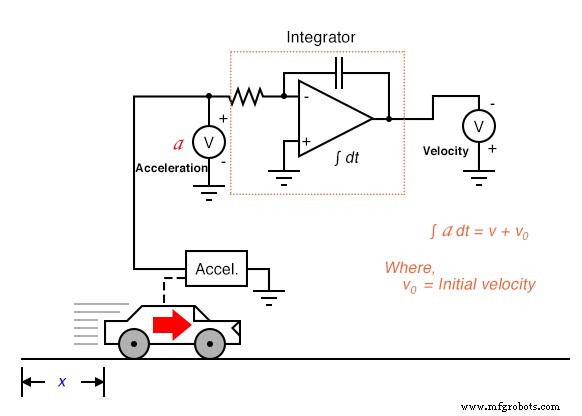
В этой системе интегратора расчетная скорость автомобиля будет действительна только в том случае, если схема интегратора инициализирована . на нулевое выходное значение, когда автомобиль неподвижен ( v =0). В противном случае интегратор вполне мог бы выдавать ненулевой сигнал для скорости ( v ₀ ), когда автомобиль неподвижен, поскольку акселерометр не может определить разницу между неподвижным состоянием (0 миль в час) и состоянием постоянной скорости (скажем, 60 миль в час, без изменений). Эта неопределенность выходного сигнала интегратора является неотъемлемой частью процесса интеграции, а не артефактом схемы или датчика.

Таким образом, если для любого физического измерения требуется максимальная точность, лучше измерить эту переменную напрямую, а не вычислять ее на основе других измерений. Это не означает, что вычисления бесполезны. Напротив, часто это единственный практический способ получить желаемое измерение. Однако для получения точных измерений необходимо понимать и соблюдать пределы вычислений.

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Рабочий лист линейных вычислительных схем