Механизм подповерхностной деформации при нанорезке арсенида галлия с использованием моделирования молекулярной динамики

Введение

Арсенид галлия (GaAs) - типичный вид соединений AIIIBV, а также один из важнейших полупроводниковых материалов. Благодаря своим прекрасным свойствам, таким как прямая запрещенная зона, высокая подвижность электронов и высокое удельное сопротивление, монокристаллический арсенид галлия находит широкое применение в различных областях, таких как инфракрасные оптические устройства и микроволновые устройства. В связи с постоянным развитием производства, строгие требования к шероховатости и точности формы поверхности, а также к внутренним повреждениям становятся все более востребованными. Технология нанорезки позволяет улучшить характеристики оптических элементов из арсенида галлия и расширить область их применения. Процесс наноразрезки кристаллов арсенида галлия сталкивается со многими трудностями, такими как хрупкое растрескивание, анизотропия и другие подповерхностные повреждения. Таким образом, исследование механизма нанорезки арсенида галлия имеет большое значение для решения проблем механической обработки, улучшения качества поверхности арсенида галлия и разработки соответствующей нанометрической технологии обработки.

Во многих исследованиях проводились наноразмерные эксперименты с арсенидом галлия. Fang et al. [1] сравнили характеристики наноиндентирования и наноцарапины арсенида галлия и кремния. Тейлор и др. [2] исследовали наноиндентирование при сверхнизкой нагрузке в арсениде галлия (100) с острием в виде куба. Брэдби и др. [3] обнаружили всплывающие события арсенида галлия в сферической выемке. Fang et al. [4, 5] исследовали свойства механической обработки мягких, хрупких полупроводников и впервые получили зеркальную поверхность из арсенида галлия методом алмазного точения. Хотя сообщалось о многих исследованиях вдавливания и физических свойств арсенида галлия, мало что известно о его процессе нанорезки и механизме образования повреждений. Это в основном из-за больших трудностей в проведении экспериментов и последующей характеризации. С одной стороны, практически невозможно проверить процесс нанорезки и измерить нанометрические данные с помощью онлайн-измерения из-за нанометрового масштаба и высокой скорости резания. С другой стороны, проведение серии экспериментов по нанометрической обработке и измерениям обходится дорого.

Моделирование молекулярной динамики (МД) - один из наиболее эффективных методов исследования механизма нанометрической обработки. Shimada et al. [6, 7] доказали, что МД моделирование является эффективным способом описания нанометрического процесса обработки. Komanduri et al. [8] обнаружили явление структурного перехода кремния в процессе нанорезки с помощью МД-моделирования. Pei et al. [9] исследовали дислокационное образование меди с помощью крупномасштабных МД-моделей нанометрической обработки. Lai et al. [10] изучали влияние критического переднего угла и деформацию материала германия при нанометрической резке, а также исследовали процесс наноразрезки с частичным перекрытием [11]. Кроме того, многомасштабный подход к моделированию получил широкое развитие в области сверхточной обработки [12,13,14]. Мультимасштабное моделирование объединяет методы моделирования в разных масштабах, такие как модель MD в наномасштабе и модель FE в нано / микромасштабе [15], для более полного и реалистичного изучения процесса обработки. В этой статье основное внимание уделяется механизму подповерхностной деформации процесса нанорезки, поэтому в качестве метода исследования выбрано моделирование МД.

Что касается исследуемых материалов, большинство исследований МД-моделирования в нанометрической обработке сосредоточено на полупроводниках, таких как кремний и германий, или металлах, таких как медь и алюминий. О численном анализе нанорезки арсенида галлия сообщалось меньше исследований. Fan et al. [16] исследовали пластический отклик арсенида галлия с помощью МД моделирования и токарных экспериментов. Йи и др. [17] исследовали фазовое превращение и анизотропию арсенида галлия в процессе наночастиц с помощью МД-моделирования. В этой статье проводится серия трехмерных МД-моделирования для исследования пластической деформации в процессе нанорезки монокристаллического арсенида галлия. Также систематически изучается влияние параметров резания, таких как скорость резания и ориентация резания.

Методы

Для изучения деформационного поведения хрупкого кристаллического арсенида галлия в процессе нанорезки созданы модели МД-моделирования. Трехмерная модель МД показана на рис. 1. Заготовка представляет собой монокристаллический арсенид галлия, кристаллизующийся в решетке цинковой обманки с атомами Ga и As, занимающими две ГЦК-подрешетки. Размер заготовки 85 нм × 30 нм × 35 нм. Модель детали состоит из трех слоев:пограничного слоя, термостатического слоя и ньютоновского слоя. Заготовка фиксируется пограничным слоем, в то время как термостатический слой устанавливается на постоянную температуру 293 K для имитации рассеивания тепла в реальном процессе обработки. Слой Ньютона - это область разреза, которая раскрывает механизм процесса нанорезки. Движение атомов в ньютоновском слое подчиняется классическому второму закону Ньютона. Чтобы имитировать алмазный инструмент в реальном процессе резания, создается модель полусферического алмазного инструмента с радиусом кромки инструмента 10 нм, а глубина резания установлена ​​на 4 нм. Алмазный инструмент настраивается на определенную скорость для врезания в заготовку. С ограничением вычислительных ресурсов модель минимизирована и упрощена, но все же убедительно объясняет пластическую деформацию и образование повреждений в нанометровом масштабе. Алмазный инструмент упрощен как полусфера для изучения поведения пластичного удаления в горизонтальном направлении, такого как боковой поток и скопление на двух сторонах инструмента, что является важными характеристиками трехмерного моделирования. Для изучения влияния параметров процесса строятся модели с разными скоростями резания и ориентациями. В таблице 1 перечислены параметры моделей.

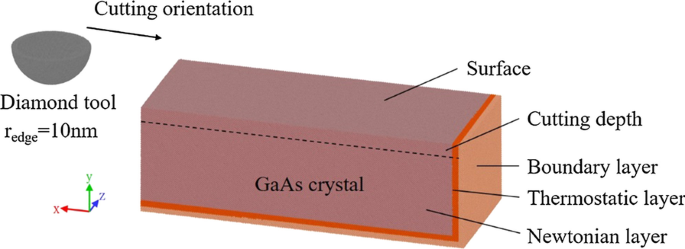
Имитационная модель МД

Потенциал - это основа для расчета силы и энергии между атомами, а также одна из самых важных настроек в моделировании МД. В предыдущем исследовании потенциальная система, состоящая из трех видов потенциала, была определена для моделирования арсенида галлия и модели алмазного инструмента [18]. В этой системе для описания взаимодействия между Ga и As используется потенциал Терсоффа-Бреннера, демонстрирующий хороший эффект моделирования [19]. Установлен экспоненциальный отталкивающий потенциал для описания взаимодействия между алмазным инструментом и заготовкой из арсенида галлия с помощью квантово-химического метода, который имеет форму упрощенного потенциала Борна – Майера [18]. В алмазном инструменте используется потенциал Терсоффа-ZBL. Потенциальная система представлена ​​на рис. 2.

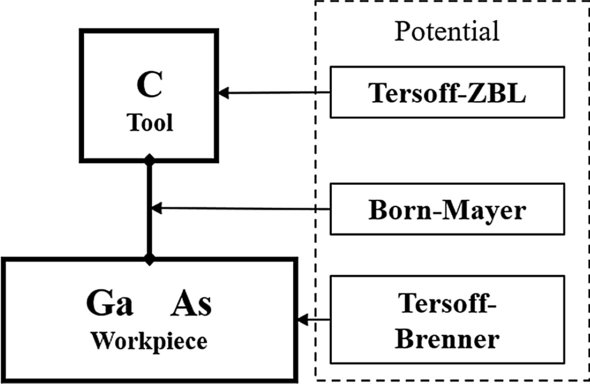
Возможная система в модели

LAMMPS используется для моделирования MD, а визуализация и анализ выполняются через OVITO, включая анализ дислокаций (DXA), расчет напряжений и анализ координации. Релаксация детали задана как ансамбль NPT, чтобы минимизировать энергию системы и стабилизировать свободную поверхность, в то время как процесс нанорезки задан как ансамбль NVE. Временной шаг для интегрирования при моделировании составляет 1,0 фс.

Результаты и обсуждение

Общее описание

Как показано на рис. 3, заготовка из арсенида галлия обрабатывается на расстоянии резания 60 нм со скоростью резания 400 м / с в направлении [\ (\ overline {1} \) 00] на (010) самолет. Заготовка окрашена в соответствии со смещением атома по y -направление. Наблюдается, как атомы перед инструментом растекаются вверх, превращаясь в стружку при экструзии. Множество атомов стекают вниз и образуют обработанную поверхность. С обеих сторон обработанной канавки атомы накапливаются на высоте 2 нм из-за выдавливания и вспашки инструмента. Результат показывает, что деформация и удаление хрупкого кристалла арсенида галлия представляет собой пластичное поведение, когда обработка осуществляется в нанометрическом масштабе. Небольшое количество кластеров арсенида, выпадающих на обработанную поверхность, очевидно в процессе моделирования. Это исследование показывает наличие выделений арсенида после отжига [20]. Потенциал Терсоффа-Бреннера позволил моделировать осаждение кластеров арсенида [19]. В процессе резки материал поверхности нагревается теплом, а затем отжигается, образуя кластеры арсенида. Однако это осаждение не является серьезной проблемой в процессе нанорезки. Поэтому эти атомы будут скрыты в последующем анализе.

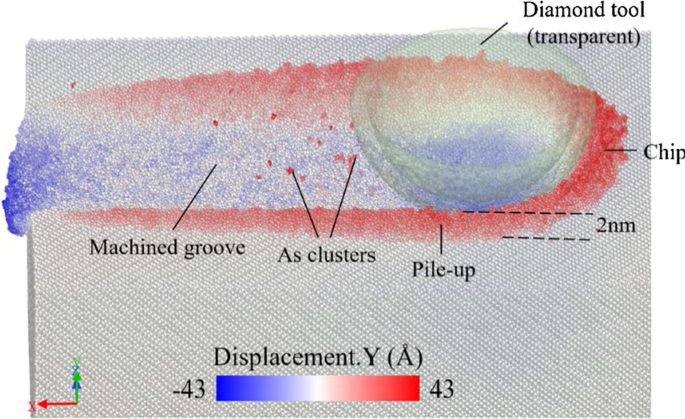
Результат моделирования нанорезки окрашен смещением атома по y -направление

Сравните кривую силы резания во время процесса обработки на рис. 4. Вначале тангенциальная сила и нормальная сила возрастают по мере врезания инструмента в материал. Боковая сила колеблется около 0, потому что силы компенсируются в z -направление. Когда силы стабилизируются, нормальная сила и касательная сила колеблются около 1700 нН и 700 нН соответственно. Обнаружено, что сила в y -направление является доминирующим в процессе резания из-за большого эффективного отрицательного переднего угла алмазного инструмента, представленного в модели. Отрицательный передний угол создает большое сжимающее напряжение, которое вызывает большую нормальную силу в процессе резания.

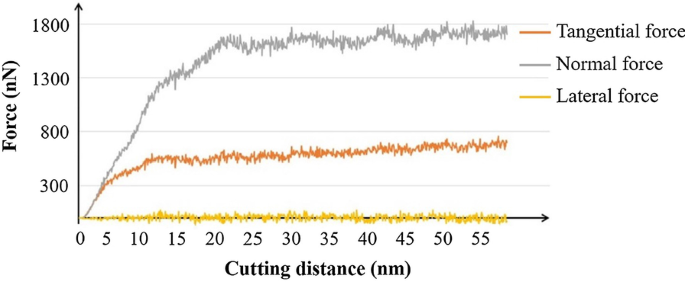
Сила резания в процессе нанорезки

Дислокации и ошибки укладки

Формирование подповерхностных повреждений - важная часть изучения механизма нанорезки. Для дальнейшей оптимизации параметров обработки необходимо выяснить механизм образования повреждений арсенида галлия во время обработки. Кристаллы обладают анизотропией атомной структуры, и это одна из самых серьезных проблем в процессе обработки, которая может повлиять на производительность процесса при различных ориентациях.

Распределение дислокаций в обрабатываемой поверхности показано на рис. 5, а движение инструмента происходит по (010) [\ (\ overline {1} \) 00] ориентации резания. Дислокации наблюдаются вокруг обработанной канавки, образуя дислокационный слой около 8 нм. В обрабатываемой поверхности присутствуют два основных типа дислокаций. Дислокации 1/2 [110] в основном скользят по двум боковым стенкам обработанной канавки, а дислокации 1/6 [112] распределяются под дном канавки. Дислокации 1/2 [110] и 1/6 [112] оказались совершенными дислокациями (синие линии) и частичными дислокациями (зеленые линии) соответственно. Образование дислокаций означает переходные движения локальных атомов, что означает, что деформация и удаление находятся в пластичном состоянии. Доказано, что хрупкий материал также демонстрирует пластичное состояние в достаточно малых масштабах.

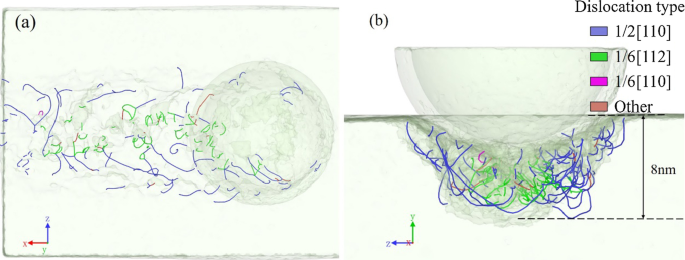
Перспективные виды распределения дислокаций в обрабатываемой геологической среде на а г -направление и b x -направление

Напряжение фон Мизеса, которое рассчитывается с учетом составляющих напряжения сдвига, обычно используется для определения образования дислокации. На рис. 6 показано поперечное сечение дислокации и распределение напряжений по Мизесу. Область высоких напряжений сосредоточена под инструментом из-за выдавливания. Когда напряжение, создаваемое инструментом, превышает предел текучести материала заготовки, материал будет скользить по поверхности скольжения, и относительное движение материала скольжения приведет к дислокациям. Следовательно, дислокации зарождаются и распространяются в монокристалл из-за высокого напряжения в зоне обработки. Локальная энергия будет высвобождена атомным движением.

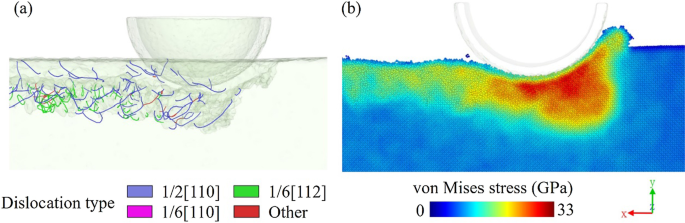
а Распространение вывиха и б Распределение напряжений по Мизесу в подповерхностной части модели наноразрезания

Дислокации в хрупких и пластичных материалах сильно различаются. Арсенид галлия представляет собой типичный хрупкий кристалл, а дислокации сосредоточены вблизи обработанной поверхности. Однако дислокации в пластичных материалах, таких как медь, будут расширяться и проскальзывать глубоко в заготовку и образовывать кластер дислокаций с высокой плотностью во время процесса резки [21], как показано на рис. 7a. Дислокации возникают в результате пластической деформации материалов. Расширение кластеров дислокаций для пластичных материалов приводит к широкому диапазону пластичных деформаций и диффузного напряжения. Однако локализация дислокаций в хрупких материалах, таких как арсенид галлия, указывает на то, что пластическая деформация происходит только вблизи поверхности без полного снятия напряжения. Когда напряжение сконцентрировано до порогового значения, могут появиться другие виды повреждений, такие как фазовые превращения или трещины. В нашем предыдущем исследовании [18] было изучено образование трещин арсенида галлия, и было обнаружено, что режим удаления изменится с пластичного с образованием дислокаций на хрупкий режим с трещинами при увеличении скорости резания. Образование дислокации снимет напряжение, которое может вызвать возникновение трещины, и в этом случае режим деформации будет иметь тенденцию к пластичности, а не к хрупкости.

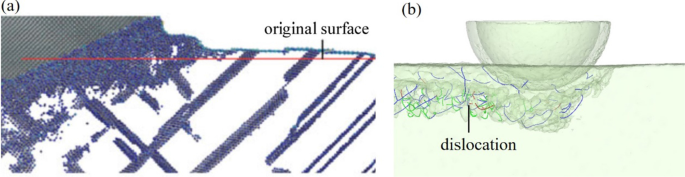
Дислокации при нанорезке различных монокристаллических материалов: a медь [21] и b арсенид галлия

На Рисунке 8 показаны дефекты упаковки, обнаруженные в обработанном слое. Атомы в заготовке окрашиваются в соответствии с координационным числом. Для удобства осмотра четырехкоординационные атомы с оригинальной структурой цинковой обманки скрыты. Можно заметить, что существуют трехкоординационные атомы, периодически размещаемые в обрабатываемой подповерхности. В сочетании с частичными дислокациями, обнаруженными под дном канавки, частичные дислокации, которые в основном выходят из границ зерен или свободных поверхностей, могут вызывать образование дефектов упаковки или двойникование [22, 23]. Дефекты упаковки в модели представляют собой не полностью дислоцированные атомные плоскости, а несколько небольших участков на границе монокристалла и аморфного слоя, поэтому частичные дислокации существуют на границах дефектов упаковки. Также можно сделать вывод, что в фактически обработанном слое могут быть дефекты упаковки.

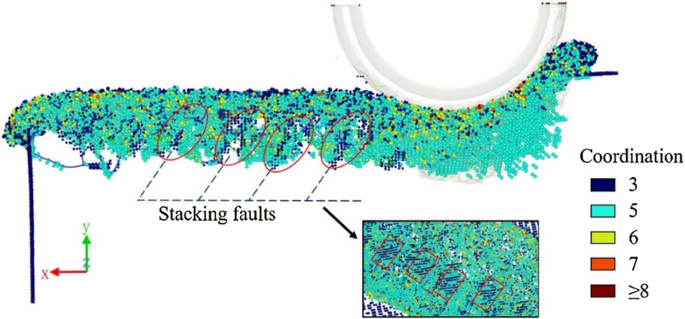
Дефекты штабелирования в обработанном слое

Фазовое преобразование и аморфизация

Структура решетки материала может измениться из-за высокого напряжения во время нанорезки. Изучая процесс фазового превращения, можно лучше понять процесс резки арсенида галлия, что полезно для оптимизации параметров процесса или при разработке эксперимента по предварительной обработке перед наноразрезкой.

Монокристаллический арсенид галлия имеет структуру цинковой обманки при нормальном давлении и температуре. Однако структура превращается в шестикоординатный GaAs-II, когда сжимающее напряжение достигает 17 ГПа [24]. Фазовое превращение заканчивается структурой вюрцита, когда напряжение превышает 60 ГПа [25].

На рис. 9а показано структурное изменение модели со скоростью резания 400 м / с при ориентации (010) [\ (\ overline {1} \) 00]. Слой обработанной области демонстрирует аморфную структуру толщиной около 6 нм без характерной структуры кристалла.

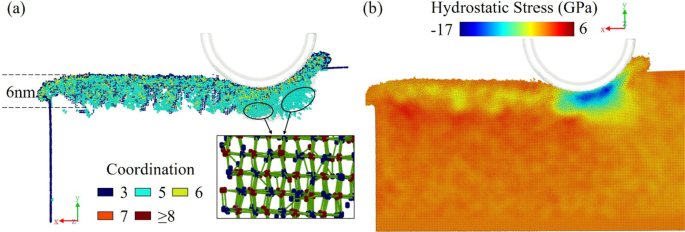
Распространение a высококоординированные атомы и пятикоординированная структура и b распределение гидростатического напряжения

Очевидно, что часть атомов в позиции обработки превращается в пятикоординационную структуру. Подобно структуре bct-5 кристалла кремния, образующегося под действием сжимающего напряжения, эта пятикоординационная структура рассматривается как промежуточная при образовании шестикоординированного GaAs-I. Гидростатическое напряжение увеличивается и вызывает искажение решетки при резке инструмента. Однако, как показано на распределении гидростатического напряжения на рис. 9b, максимальное гидростатическое напряжение составляет 17 ГПа, что как раз достигает критического значения преобразования из GaAs-I в GaAs-II. Подповерхностная область, где гидростатическое напряжение превышает 17 ГПа, очень мала, и большая часть площади заготовки имеет гидростатическое напряжение ниже порога перехода. В результате трудно найти большие куски атомов с шестикоординированной структурой, а пятикоординационная структура является промежуточной фазой от GaAs-I к GaAs-II.

На рисунке 10 показаны кривые функции радиального распределения для выбранной области в процессе резания, то есть области под алмазным инструментом. Рассчитываются кривые радиального распределения до, во время и после обработки. Заготовка вначале имеет упорядоченную структуру цинковой обманки, кривая которой состоит из регулярных пиков. Когда алмазный инструмент достигает выбранной области, функция радиального распределения показывает неупорядоченное состояние как в ближнем, так и в дальнем диапазоне. Это подразумевает наличие сильной аморфизации с неупорядоченным расположением атомов в области. Однако кривая обработанной поверхности подразумевает, что структура может восстанавливаться и становится упорядоченной на коротком расстоянии и неупорядоченной на большом расстоянии. При снятии напряжения материал изменит структуру на структуру с минимальным энергетическим состоянием. Атомы с промежуточной фазой могут переходить в аморфное или другое состояние. Таким образом, кривая показывает стабильное состояние после механической обработки с аморфным арсенидом галлия. Можно обнаружить, что в процессе обработки есть боковой пик на 3,3 Å, и пик исчезает, когда инструмент выходит. Это явление свидетельствует об образовании и исчезновении промежуточной фазы, которую можно рассматривать как упругую деформацию в процессе резания. Без усилия инструмента часть атомов восстановится до структуры цинковой обманки, а другие перейдут в другую стабильную фазу или аморфное состояние, что представляет собой постоянную пластичную деформацию.

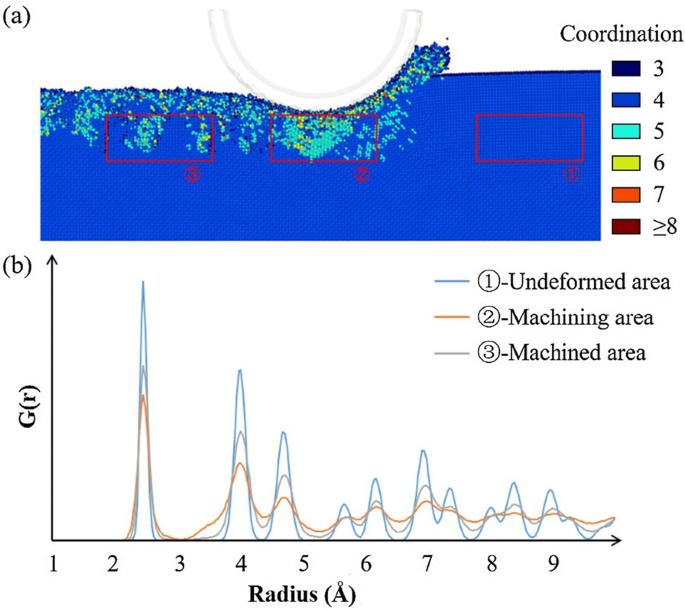
Функция радиального распределения выбранной площади: a избранные районы; б соответствующие кривые радиальной функции распределения

Влияние скорости резания и ориентации на деформацию подповерхностных слоев

На формирование поверхностных / подповерхностных повреждений влияет множество факторов, и различные параметры резки будут влиять на формирование дислокации.

Распределение дислокаций при разных скоростях резания сравнивается на рис. 11a – c. Плотность дислокаций постепенно уменьшается с увеличением скорости резания. Обработанная поверхность богато дислокациями, особенно при скорости резания до 200 м / с. Когда процесс резания происходит с высокой скоростью деформации, времени для зарождения и распространения дислокаций недостаточно. В результате количество дислокаций меньше, и пластическая деформация, вызываемая дислокациями, также становится менее доминирующей. Материал будет быстро деформироваться и дезорганизоваться, время восстановления также будет коротким, и будет легче сформировать аморфные атомы с нерегулярной структурой. Следовательно, более высокая скорость резания - это способ сдержать образование дислокаций. На рис. 11d – f представлены поперечные сечения распределения напряжений по Мизесу в трех соответствующих моделях. При более высокой скорости резания напряжение материала вблизи инструмента относительно выше из-за большой энергии резания. По сравнению с тремя моделями, модель 800 м / с имеет более высокую концентрацию напряжений перед инструментом, а обработанная подповерхность представляет собой более непрерывную область напряжений с более высокими значениями. Напротив, в низкоскоростных моделях напряжение снимается из-за образования дислокаций. Пластическая деформация, вызванная дислокациями, высвобождает энергию локальной деформации и напряжение, вызванное изгибом и упругой деформацией решетки. Следовательно, в заготовке с более высокой скоростью резания напряженное состояние может быть серьезным из-за отсутствия дислокаций, что облегчает образование трещин в процессе резки.

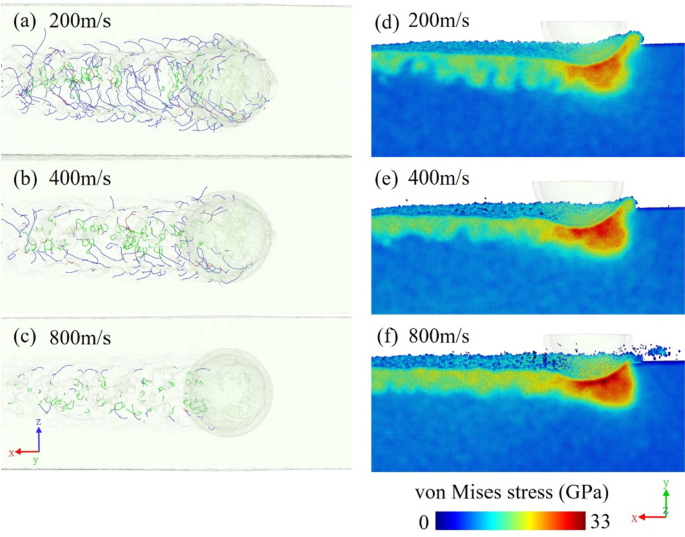
Перспективные виды распределения дислокаций и распределения напряжения по Мизесу в моделях с различными скоростями резания a , d 200 м / с, b , e 400 м / с и c , f 800 м / с

Анизотропия - серьезная проблема в процессе наноразрезки кристаллов [26, 27], в том числе монокристаллического арсенида галлия. Из-за своей монокристаллической структуры кристалл арсенида галлия проявляет различные свойства в различных ориентациях кристаллов. Для изучения анизотропии построены три модели с разными плоскостями отсечения и ориентацией. Ориентация разреза:(010) [\ (\ overline {1} \) 00], (\ (\ overline {1} \) 10) [\ (\ overline {1} \) \ (\ overline {1} \ ) 0] и \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \). Рисунки 12a – f отражают большие различия, существующие между распределениями дислокаций. Как указано выше, в модели (010) [\ (\ overline {1} \) 00] существуют два типа дислокаций. Когда направление резания соответствует направлению \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \), большинство дислокаций находится в нижней части обработанной канавки, в то время как некоторые сгруппированные дислокации выходят на поверхность перед инструментом. На рис. 12б с обеих сторон боковой стенки обнаружено несколько дислокаций. При ориентации резания \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) наблюдаются древовидные дислокации, идущие от середины к обеим сторонам. , покрывающего обработанную поверхность, как показано на рис. 12c. Однако, в отличие от первой модели, есть несколько частичных дислокаций в \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) и \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) модели, и большинство дислокаций являются идеальными дислокациями вдоль ориентации [110]. Точно так же дефекты укладки не обнаруживаются в обработанной зоне \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) и \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) модели, соответствующие отсутствию частичных дислокаций. Это также доказывает эффект анизотропии материала.

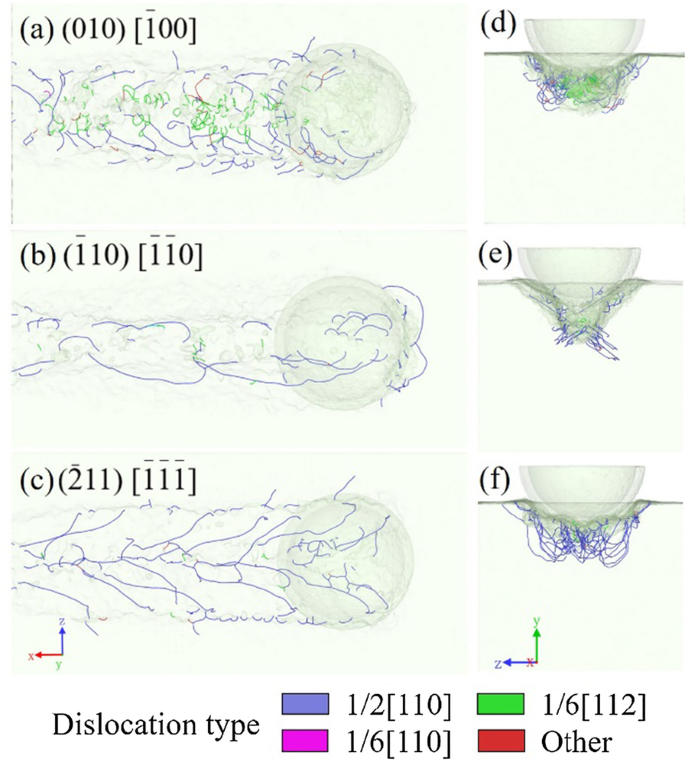
Перспективные виды распределения дислокаций в моделях с ориентацией разреза по a , d \ ((010) \, [\ overline {1} 00] \), b , e \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) и c , f \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \)

На рис. 13a – f сравнивается распределение дислокаций и распределение напряжений по Мизесу для трех моделей с разной ориентацией резания. Ориентация кристалла оказывает очевидное влияние на распространение напряжения. В моделях (010) [\ (\ overline {1} \) 00] и \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) , напряжение сосредоточено перед алмазным инструментом, но направления расширения различны. Однако область сосредоточенного напряжения модели \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) шире, а область высокого напряжения перед инструментом распространяется на поверхность. Из-за разницы в ориентации кристаллов компоненты напряжения вдоль направления скольжения будут разными, что приведет к различному внешнему виду дислокаций. Когда угол направления напряжения и поверхности скольжения мал, скольжение более вероятно, и материал будет деформироваться в пластичном режиме. Напротив, трещина и хрупкое разрушение имеют тенденцию к возникновению, когда отношение растягивающего напряжения, перпендикулярного плоскости спайности, к напряжению сдвига вдоль плоскости скольжения увеличивается.

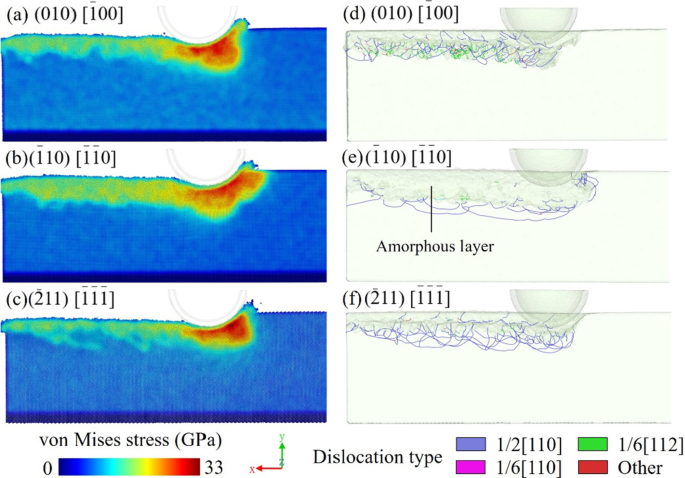
Распределение напряжений по фон Мизесу и распределение дислокаций в моделях с ориентацией резания вдоль a , d \ ((010) \, [\ overline {1} 00] \), b , e \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) и c , f \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \)

Сравнивая распределение напряжения и дислокации, модели с более высокой плотностью дислокаций могут иметь более низкое напряжение в обрабатываемой поверхности. На рисунке 13e показан более толстый слой аморфных повреждений в подповерхностной части модели \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \), который соответствует плотным областям дислокаций в другие модели. Это явление показывает, что анизотропия может влиять на типы повреждений. В модели \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) трудно снять сосредоточенное напряжение из-за меньшего образования дислокаций. В результате при сильном напряженном состоянии расположение атомов нарушается. Диапазон напряжений больше в обрабатываемом слое, а остаточное напряжение выше. Напротив, модель \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) имеет более тонкий слой напряжений в обрабатываемой подповерхности из-за большего плотность дислокаций. Образование дислокации снимает часть напряжения в процессе резки. В предыдущем исследовании [18], когда режим пластического повреждения переходит с дислокации на аморфизацию, обработанная подповерхность демонстрирует состояние сильного напряжения и аморфное повреждение. Подповерхностные трещины легче образуются на границе аморфного кристалла и монокристалла. Можно сделать вывод, что трещины более вероятны, если ориентация резания находится в направлении \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \). Образование дислокации может уменьшить образование хрупких повреждений. Помимо механизма скола, это также причина того, почему на образование трещин влияет анизотропия.

В процессе резки материал рядом с режущим инструментом подвергается высоким напряжениям и сильному сжатию, что вызывает структурные изменения материала, такие как фазовое превращение и аморфизация. Под аморфным слоем проскальзывание будет происходить на большей площади, и в монокристалле будут образовываться дислокации из-за широко распространенных эффектов напряжения. Это основные пластические деформации при нанорезке арсенида галлия. Различные условия резания будут влиять на локальное напряженное состояние и легкость образования дислокаций. Когда образование дислокаций затруднено из-за высокой скорости обработки или анизотропии, режим пластической деформации будет иметь тенденцию к преобладанию аморфной формы из-за аморфизации, вызванной невыполненным напряжением. В этой ситуации также легко образуется трещина. Напротив, дислокации будут основным компонентом пластической деформации, если условия подходят для скольжения материала.

Conclusion

MD simulation is used to study the mechanism of damage formation in the nano-cutting process of gallium arsenide crystal. The atomic motion and cutting force of the process are also analyzed. The dislocation, stacking fault, and phase transformation are mainly studied as the surface/subsurface damages. The conclusions can be summarized as follows:

1. 1.

   In the nano-cutting of gallium arsenide, the dislocation and structural transformation are found as the main deformation mechanism in the machined subsurface.

2. 2.

   Dislocations and stacking faults are observed in the machined subsurface groove, and the formations of stacking faults and partial dislocations are consistent.

3. 3.

   An intermediate phase with five-coordination is found in front of the tool because hydrostatic stress is close to but not higher than the transition threshold (17 GPa). An amorphous layer forms in the machined subsurface.

4. 4.

   With increasing cutting speed, the dislocation density decreases because of the high strain rate. Anisotropy has a great effect on the dislocation type and density. Partial dislocations are easier to form in the (010) [\(\overline{1}\)00] model. Moreover, the \((\overline{1}10)\,[\overline{1}\overline{1}0]\) model has a lower dislocation density and a more severe amorphization.

Доступность данных и материалов

The datasets generated or analysed during the current study are not publicly available due the data also forms part of an ongoing study, but are available from the corresponding author on reasonable request.

Сокращения

MD:

Molecular dynamics

GaAs:

Gallium arsenide

FE:

Finite element

FCC:

Face centered cubic

Tersoff-ZBL:

Tersoff-Ziegler–Biersack–Littmark

LAMMPS:

Large-scale atomic/molecular massively parallel simulator

OVITO:

Open visualization tool

NPT:

Number-pressure–temperature, isothermal-isobaric ensemble

NVE:

Number-volume-energy, microcanonical ensemble