Свойства геометрической фазы в электромеханических колебаниях нанопроволочных резонаторов на основе углеродных нанотрубок

Введение

Механические колебания мельчайших резонаторов, таких как нанопроволоки на основе углеродных нанотрубок (УНТ) [1–3], полупроводниковые нанопроволоки [4], графены [5] и левитирующие частицы [6], были основным предметом исследования. в сообществе нанонауок более десяти лет. Активные исследования электромеханических колебаний резонаторов из нанопроволоки, возбуждаемых внешней периодической силой, проводились как в теоретической, так и в экспериментальной сферах. В частности, резонаторы на основе нанопроволоки на основе УНТ вызывают значительный интерес в качестве механических устройств наноразмеров из-за их необычайной чувствительности с высокими факторами качества к небольшим возмущениям из окружающей среды. Подвесные резонаторы на основе нанопроволок на основе УНТ являются многообещающими кандидатами для устройств, измеряющих широкий диапазон физических величин, таких как электромагнитные волны [2], малые силы [7], массы [8], температуры [9] и шумы [10]. / P>

Анализ квантовой эволюции фазы в колебаниях нанопроволоки необходим для теоретического выяснения основных особенностей системы. Что касается квантовых колебательных состояний резонаторов на основе нанопроволок на основе УНТ [11], геометрическая фаза [12], как и обычная динамическая фаза, возникает как дополнительная эволюция фазы. Геометрическая фаза [12] представляет собой анголономию квантового состояния, которая может быть применима в различных областях физики. Анализ геометрической фазы может быть потенциально использован для характеристики наносвойств нанопроволок, таких как резонансные профили [13, 14], сильные квантовые колебания [15, 16], механизмы релаксации деформации [17, 18], появление магнитоплазмонов Дирака. [19] и топология осцилляций Ааронова-Бома [20].

Изучение геометрической фазы, связанной с неадиабатической динамикой, может дать представление о наномеханических системах, что необходимо для развития точных методов моделирования [21]. Подготовка, манипулирование и обнаружение квантовых состояний являются важными факторами в квантовых технологиях. Цель настоящего исследования - пролить свет на поведение геометрической фазы во времени, которая имеет место в квантовых состояниях колебаний нанопроволоки. Чтобы понять механизм колебаний нанопроволоки на основе УНТ, мы исследуем временную эволюцию геометрической фазы в сжатом состоянии, которое является квантовым состоянием классического типа, таким как когерентное состояние. Достоинство сжатого состояния состоит в том, что неопределенность квадратуры в этом состоянии может быть существенно уменьшена за счет увеличения неопределенности другой квадратуры, в то время как такая модуляция неопределенности невозможна в когерентном состоянии. В частности, мы проанализируем влияние резонанса на геометрическую фазу. Поскольку резонансная энергия существенно отличается от энергии нерезонансного состояния [22, 23], топологическое поведение волновой функции нетривиально и может значительно отличаться от такового в нормальных ситуациях. Также будет тщательно проанализировано влияние изменения физических параметров и параметров сжатия на эволюцию геометрической фазы. Геометрические фазы широко распространены в динамических системах [24] и могут применяться в различных современных технологиях, таких как квантовые вычисления [25], интерферометрии интенсивности [26], фотонная многозадачность [27], протоколы квантового зондирования [28] и волновые -стабильность измерения [29].

Гамильтониан системы включает функции времени, связанные с затуханием системы и внешней движущей силой. Следовательно, система представляет собой разновидность гамильтоновых систем, зависящих от времени (TDHS), квантово-механические проблемы которых широко изучаются до недавнего времени. Функция времени в гамильтониане TDHS не может быть отделена от функции канонических переменных в большинстве случаев, что приводит к тому, что традиционный метод разделения переменных для решения уравнения Шредингера недоступен. Альтернативным мощным методом, разработанным для преодоления этой трудности, является метод инвариантных операторов, введенный Льюисом и Ризенфельдом [30, 31]. Этот метод является очень полезным математическим инструментом, когда мы получаем квантовые решения TDHS. На основе этого метода исследуются многие квантово-механические задачи, описываемые TDHS. Например, они включают хаотическое рассеяние частиц [32], распространение света в изменяющихся во времени средах [33], управление захваченными электронами [34] и неклассичность квантовых наноэлектронных схем [35]. Существует множество других методов квантово-механической обработки TDHS, включая метод унитарных преобразований [36], алгебраический метод Ли [37] и метод гамильтонова оценки [38].

Учитывая, что система является TDHS, мы используем метод инвариантного оператора, чтобы получить квантовые решения системы. Будет введен линейный инвариантный оператор, который представлен в терминах оператора уничтожения. Хотя операторы уничтожения и рождения представлены в терминах времени из-за временной зависимости системы, как когерентные, так и сжатые состояния могут быть получены с использованием этих лестничных операторов. Геометрическая фаза системы будет аналитически оценена с использованием волновой функции в сжатом состоянии. Временная эволюция геометрической фазы будет подробно проанализирована на основе ее иллюстраций, изображенных с различным выбором параметров.

Методы

Чтобы исследовать геометрическую фазу, нам сначала нужно установить классическое уравнение движения кончика нанопроволоки. Поскольку геометрическая фаза появляется в квантовой волновой эволюции TDHS, необходимо вывести волновые функции в конкретном квантовом состоянии, которым мы управляем. Мы рассмотрим сжатое состояние, как упоминалось во вводной части. Волновые функции в различных квантовых состояниях TDHS, включая сжатое состояние, могут быть получены с помощью метода инвариантных операторов.

Уравнение движения для зависящей от времени амплитуды x для изгибного режима подвешенной углеродной нанотрубки с эффективной массой м дается [1]

где ω ₀ резонансная угловая частота, Q добротность, f _d электростатическая движущая сила, деленная на м , η коэффициент нелинейного затухания и β Параметр Дуффинга. Для удобства предположим, что смещение острия достаточно мало относительно длины проволоки УНТ. Тогда мы можем пренебречь нелинейными членами в уравнении. (1), что приводит к [2]

Гамильтониан системы, которая дает Ур. (2) дается

где γ = ω ₀ / Q . Классическое решение уравнения. (2) состоит из дополнительной функции X _c ( т ) и частное решение X _p ( т ), которые даются

где X _{c , 0} - константа, \ (\ Omega =\ sqrt {\ omega _ {0} ^ {2} - \ gamma ^ {2} / 4} \), φ - произвольная фаза, и

Классическое решение в импульсном пространстве дается аналогичным образом, где дополнительная функция равна \ (P_ {c} (t) =me ^ {\ gamma t} \ dot {X} _ {c} (t) \) и частным решением является \ (P_ {p} (t) =me ^ {\ gamma t} \ dot {X} _ {p} (t) \). Чтобы исследовать геометрическую фазу системы, нам сначала нужно получить квантовые решения. Обратите внимание, что гамильтониан системы, представленной в формуле. (3) явно зависит от времени. Чтобы получить квантовые решения системы, мы используем метод инвариантного оператора [30, 31], который является полезным методом, когда мы рассматриваем такую ​​изменяющуюся во времени систему. Инвариантный оператор \ (\ hat {I} \) системы может быть получен из уравнения Лиувилля-фон Неймана, которое задается формулой \ ({d \ hat {I}} / {dt} ={\ partial \ hat {I}} / {\ partial t} + \ left [\ hat {I}, \ hat {H} \ right] / \ left (i \ hbar \ right) =0 \). Следовательно, из строгой оценки после вставки уравнения. (3) в это уравнение имеем линейный инвариантный оператор [34] вида

где \ (\ hat {A} \) - оператор уничтожения, который задается

Эрмитово сопряженный к уравнению. (9), \ (\ hat {A} ^ {\ dagger} \), является оператором создания.

Мы можем выразить уравнение собственных значений \ (\ hat {A} \) как

Оценивая приведенное выше уравнение, мы получаем выражение собственного значения, такое что

где A (0) = А ₀ е ^{- я φ} с

Пока когерентное состояние | A 〉 - это собственное состояние оператора \ (\ hat {A} \), сжатое состояние - это собственное состояние оператора \ (\ hat {B} \), которое задается

где μ и ν сложные переменные, которые дают уравнение

Если мы запишем уравнение собственных значений \ (\ hat {B} \) в виде

| B 〉 - сжатое состояние. Решая это уравнение в конфигурационном пространстве, мы имеем

Таким образом, волновая функция в сжатом состоянии была получена, как указано в формуле. (16). Квантовые особенности системы могут быть выяснены на основе такого аналитического описания волновой функции. Для μ =1 и ν =0, уравнение. (16) сводится к волновой функции в когерентном состоянии, которое является собственным состоянием уравнения. (10) в конфигурационном пространстве. Волновая функция, уравнение. (16) будет использоваться в следующем разделе для получения геометрической фазы в сжатом состоянии.

Результаты и обсуждение

Хорошо известно, что фаза эволюции квантовой волны включает геометрическую фазу, а также динамическую фазу. Геометрическая фаза была впервые обнаружена Берри в 1984 году [12] для системы, циклически развивающейся с адиабатическим изменением. Согласно адиабатической теореме в квантовой механике, мгновенное собственное состояние квантового состояния в циклической эволюции в пространстве параметров останется в том же состоянии позже, в то время как происходит дополнительное накопление квантовой фазы, которая является фазой Берри. Обобщение фазы Берри таким образом, что она включает неадиабатическую, нециклическую и / или неунитарную эволюцию квантовой системы, является геометрической фазой.

Геометрическая фаза в сжатом состоянии определяется как

Дифференцирование волновой функции по времени в конфигурационном пространстве становится

где

Дальнейшая оценка после вставки уравнения. (18) в уравнение. (17) дает

где

Последний член в g ₅ содержащий ( μ - μ ^∗ ) ( ν - ν ^∗ ) неадекватна как фаза, потому что это чисто мнимое число. Следовательно, теперь мы удалим этот член, выбрав хотя бы один из μ и ν как реальную ценность. Это средство всегда можно сделать без потери общности, потому что только относительная фаза между μ и ν имеет физический смысл, а не их абсолютные фазы.

Из выполнения интегрирования в формуле. (22) имеем

где \ (\ bar {g} _ {i} (t) ~ (i =3,4,5) \) задаются как

с

Таким образом, мы оценили полную геометрическую фазу в сжатом состоянии, которое дается формулой. (28) с уравнениями. (23), (24) и (29) - (32).

Временная эволюция геометрической фазы проиллюстрирована на рис. 1, 2, 3 и 4. Из рис. 1 мы видим, что геометрическая фаза колеблется, и огибающая таких колебаний со временем увеличивается. Увеличение конверта больше, когда A ₀ большой. Характер колебаний постепенно становится неравномерным по мере того, как значения μ и ν увеличивать. Более того, амплитуда колебаний со временем увеличивается.

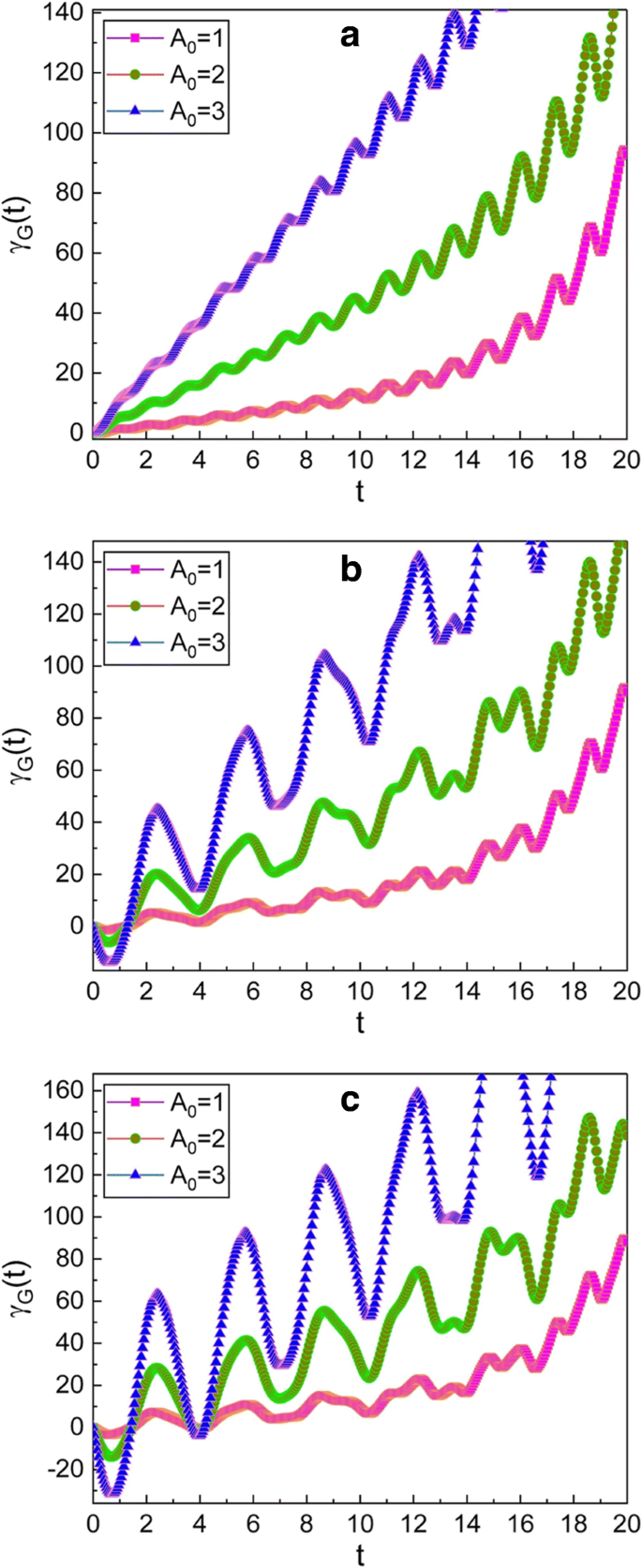
Временная эволюция геометрической фазы для нескольких различных значений A ₀ . Значения ( μ , ν ), используемые в графике, - (1, 0) для a , (\ (\ sqrt {2} \), 1) для b и (\ (\ sqrt {3} \), \ (\ sqrt {2} \)) для c . Мы использовали м =1, ω ₀ =1, ω =5, γ =0,35, f _d =1, \ (\ hbar =1 \), φ =0 и γ _G (0) =0. Фаза и все параметры для удобства приняты безразмерными, и это соглашение будет также применяться к последующим фигурам. Потому что A ₀ дается в терминах классической амплитуды X _{c , 0} дополнительной функции [см. (12)], мы можем подтвердить из графиков, что геометрическая фаза велика, когда амплитуда колебаний велика. Мы также видим, что колебание γ _G ( т ) становится большим по мере того, как значения μ и ν увеличиваются при условии, приведенном в формуле. (14)

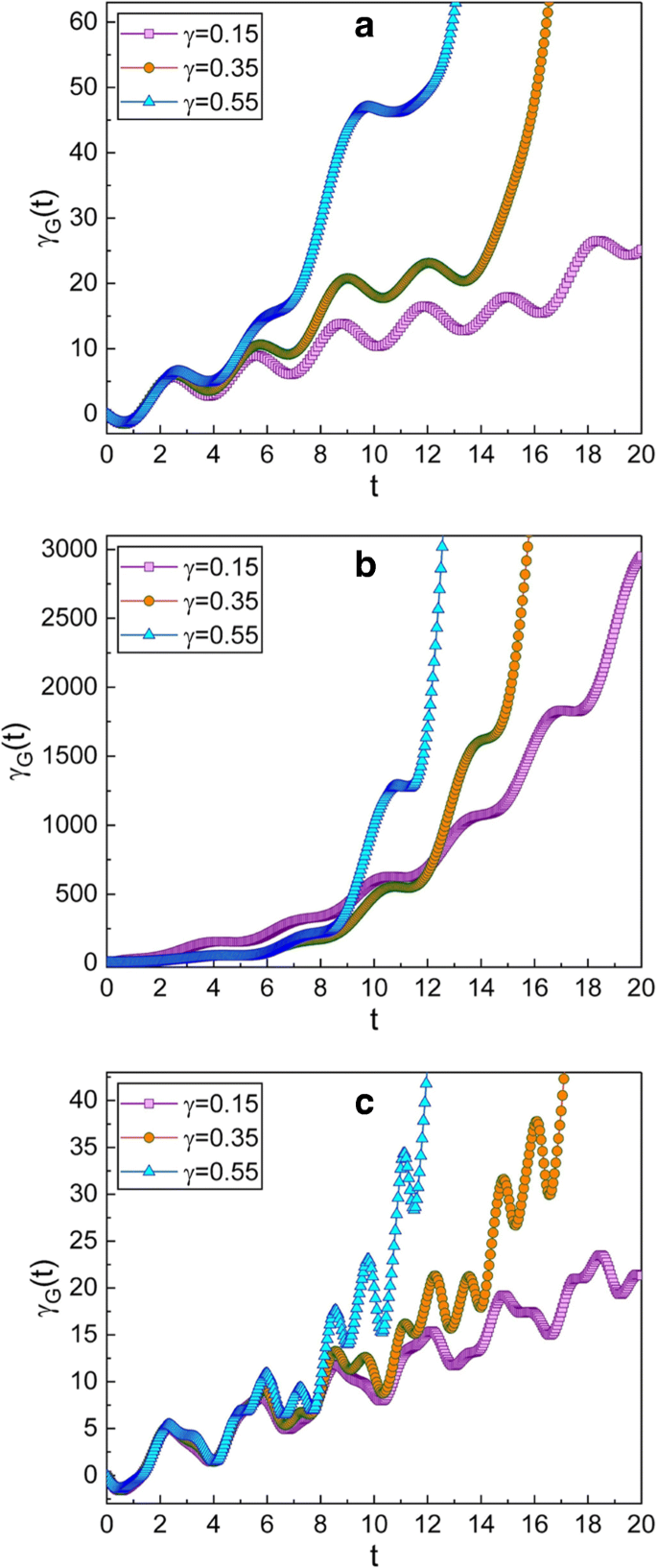
Временная эволюция геометрической фазы для нескольких различных значений γ . Значение ω в рисунках используется значение 0,3 для a , 0,99 для b и 5 для c . Выбранные здесь параметры сжатия:\ (\ mu =\ sqrt {2} \) и ν =1; этот выбор дает q -сжатое состояние в начальный момент времени. Другие использованные нами количества: м =1, ω ₀ =1, A ₀ =1, f _d =1, \ (\ hbar =1 \), φ =0 и γ _G (0) =0. Мы подтверждаем, что геометрическая фаза велика, когда коэффициент затухания γ в большинстве случаев большая, но не во всех. Частота случая б близка к резонансной частоте, тогда как частоты a и c далеки от резонансного. Геометрическая фаза для резонансного случая ( b ) очень быстро увеличивается со временем

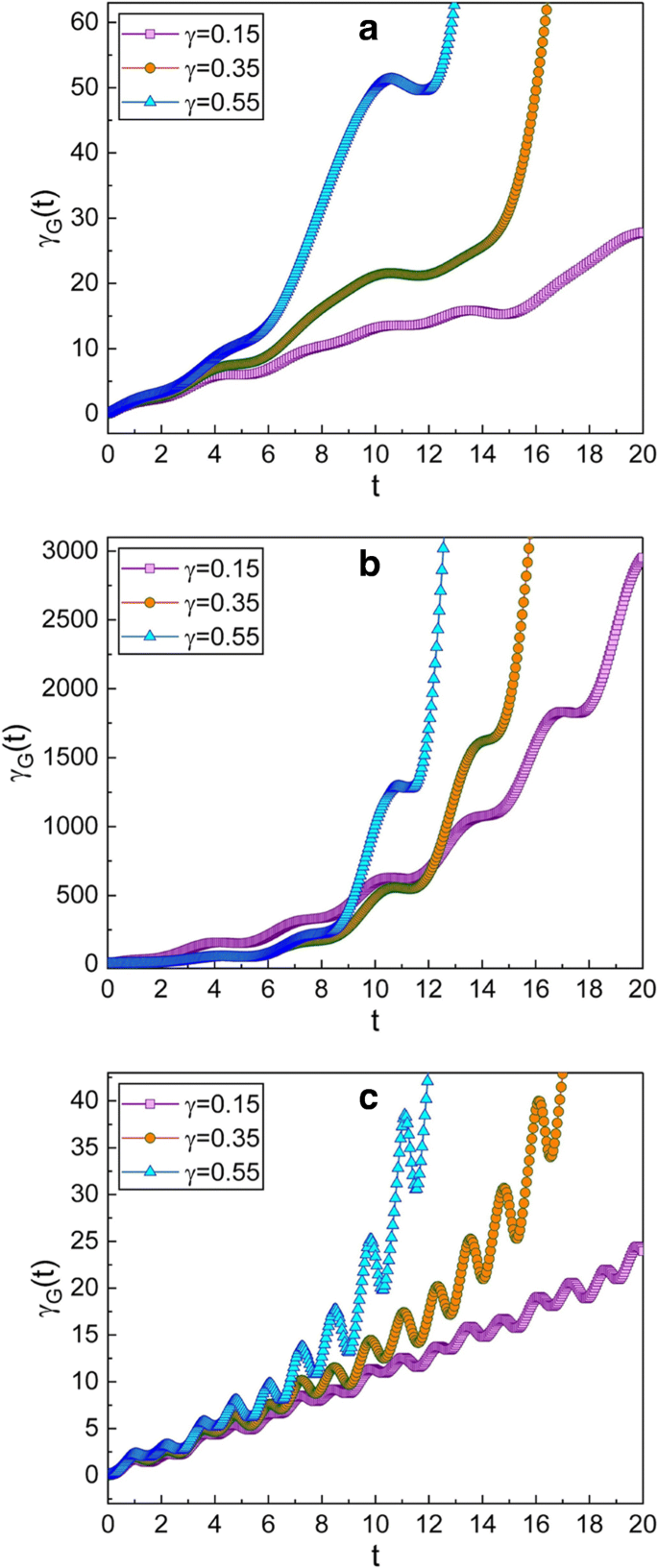
а - c Этот рисунок такой же, как на рис. 2, но для случая, когда выбранные параметры сжатия - \ (\ mu =\ sqrt {2} \) и ν =−1, что дает p -сжатое состояние в начальный момент времени. Из того факта, что общая графика в этом случае не так сильно отличается от соответствующих графиков на рис. 2, мы можем подтвердить, что эволюция γ _G ( т ) практически не имеет отношения к типам сжатия, пока абсолютные значения μ и ν не менять

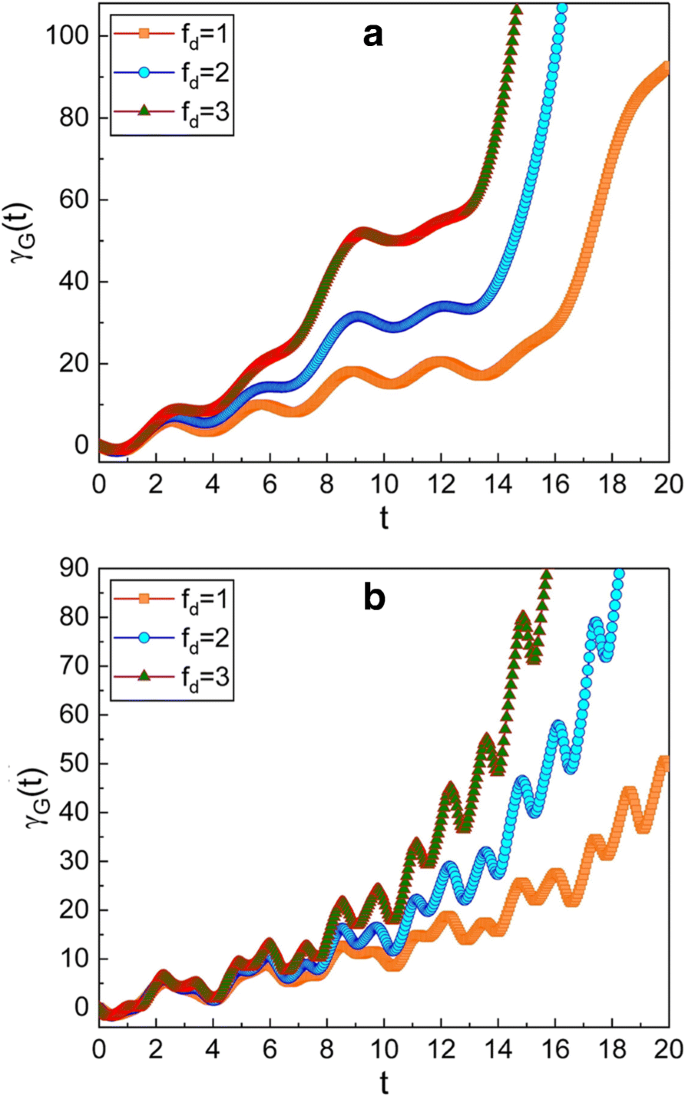
Временная эволюция геометрической фазы для нескольких различных значений f _d . Значение ω в рисунках используется значение 0,3 для a и 5 для b . Мы использовали \ (\ mu =\ sqrt {2} \), ν =1, м =1, ω ₀ =1, γ =0,3, A ₀ =1, \ (\ hbar =1 \), φ =0 и γ _G (0) =0. Поскольку амплитуда ( f _d ) движущей силы увеличивается, геометрическая фаза становится большой

Эффекты сжатия в сжатом состоянии в зависимости от параметра сжатия c где c = мк / ν был исследован в исх. [39]. Согласно анализу, приведенному в исх. [39] (см. Рис. 1 (a) в [39]) сжатое состояние, проиллюстрированное на рис. 2, которое соответствует \ (c =\ sqrt {2} \), является q -сжатое состояние в начальный момент времени, а состояние на рис. 3, которое соответствует \ (c =- \ sqrt {2} \), является p -сжатое состояние в такой же ситуации. Сравнивая рис. 2 и 3 друг к другу, можно сделать вывод, что геометрическая фаза в q -сжатое состояние почти такое же, как в p -сжатое состояние.