Два метода линеаризации мостов резистивных датчиков

Измерение незначительных изменений сопротивления в резистивных датчиках может быть сложной задачей. Вот два аппаратных метода устранения ошибок нелинейности моста.

Сопротивление резистивного датчика зависит от физической переменной, такой как температура или сила. Изменение сопротивления этих устройств в процентах обычно невелико. Например, общее изменение сопротивления тензодатчика может быть менее 1% во всем рабочем диапазоне.

Для распознавания этих малых значений требуются высокоточные измерительные схемы. Мостовые схемы позволяют нам более легко выполнять эти точные измерения. Однако выход мостовой схемы может иметь нелинейную зависимость от измеряемой физической переменной, даже если мы используем линейный датчик.

В этих случаях мы можем использовать программные или аппаратные средства для устранения ошибок нелинейности моста. В этой статье мы рассмотрим два разных метода линеаризации мостов резистивных датчиков.

Мостовая нелинейность резистивных датчиков

Рассмотрим резистивный датчик давления со следующей линейной характеристикой:

\ [R_ {sensor} =R_0 + Mx \]

где R ₀ - начальное сопротивление датчика при нулевом давлении, x - значение измеряемой величины (давления), а M - крутизна отклика датчика. Чтобы упростить наши будущие уравнения, предположим, что значение M равно значению начального сопротивления датчика (R ₀ ) и, следовательно, ответ датчика равен \ [R_0 (1 + x) \].

Обычно процентное изменение сопротивления резистивного датчика невелико, и нам нужно использовать мостовую схему, чтобы упростить выполнение точных измерений. Типичная конфигурация моста для этого датчика изображена на рисунке 1.

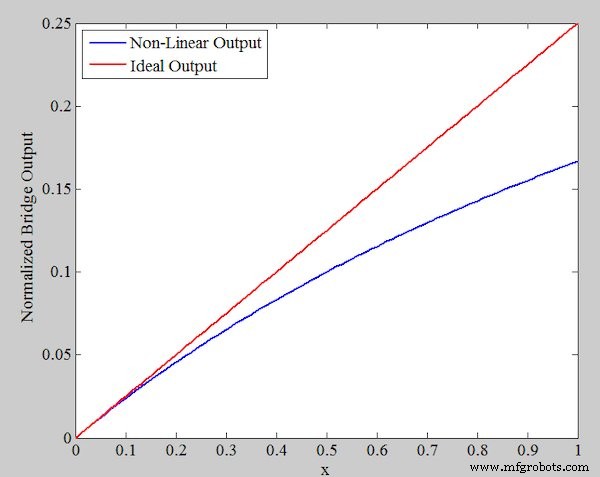
Рисунок 1. Общая мостовая конфигурация резистивного датчика

Обратите внимание, что остальные три резистора моста имеют сопротивление R ₀ . . Такой выбор мостовых резисторов максимизирует чувствительность выхода (V _out ) к изменению сопротивления датчика. Выходное уравнение можно получить как:

\ [V_ {out} =V_A - V_B =V_r \ left (\ frac {R_0 (1 + x)} {R_0 + R_0 (1 + x)} - \ frac {1} {2} \ right) \]

Это упрощает:

\ [V_ {out} =V_r \ left (\ frac {x} {2 (2 + x)} \ right) \]

Уравнение 1.

Как видите, зависимость между выходом моста и изменением значения сопротивления (x) не является линейной. Используя \ [x \ ll2 \], мы можем аппроксимировать приведенное выше уравнение следующей линейной зависимостью:

\ [V_ {out} \ приблизительно V_r \ left (\ frac {x} {4} \ right) \]

Уравнение 2.

На рисунке 2 показан нормализованный выходной сигнал моста \ [\ frac {V_ {out}} {V_r} \] как для реального случая (уравнение 1), так и для идеального выхода (уравнение 2).

Рисунок 2. Нелинейные (синий) и идеальный (красный) выходы уравнений 1 и 2

Как и ожидалось, отклонение от линейного отклика увеличивается с увеличением x.

Насколько велика ошибка нелинейности?

Оценим погрешность нелинейности вышеупомянутой мостовой схемы. Мы можем переписать уравнение 1 как:

\ [V_ {out} =V_r \ left (\ frac {x} {4} \ right) \ left (\ frac {1} {1+ \ frac {x} {2}} \ справа) \]

Если предположить, что \ [\ frac {x} {2} <<1 \], мы можем использовать теорему Тейлора, чтобы получить приближение вышеуказанной функции как:

\ [V_ {out} =V_r \ left (\ frac {x} {4} \ right) \ left (1 - \ frac {x} {2} \ right) \]

Сравнивая этот результат с уравнением 2, мы можем вычислить величину ошибки как:

\ [E_ {Non-Linearity} =V_r \ left (\ frac {x} {4} \ right) \ left (\ frac {x} {2} \ right) \]

Разделив это на ожидаемое идеальное значение, заданное уравнением 2, мы можем получить процентную погрешность линейности конечной точки для заданного изменения сопротивления (x):

\ [Percentage ~ Error =\ frac {x} {2} \ times 100 \% \]

Пример вычисления ошибки нелинейности

Рассмотрим датчик с реакцией \ [R_ {sensor} =R_0 (1 + x) \]. Предположим, что \ [R_0 =100 ~ \ Omega \] и максимальное значение x во всем рабочем диапазоне составляет 0,01. Максимальный процент ошибки линейности составит:

\ [Percentage ~ Error =\ left (\ frac {0,01} {2} \ right) \ times 100 \% =0,5 \% \]

Обратите внимание, что, хотя мы могли бы использовать программное обеспечение для удаления ошибок линейности датчика, наличие линейного отклика желательно, поскольку оно увеличивает точность измерения и облегчает калибровку системы. Существуют различные топологии схем, которые можно использовать для линеаризации мостовых схем.

В оставшейся части статьи мы рассмотрим два разных метода линеаризации мостовидных протезов.

Метод 1. Создание напряжения, пропорционального изменениям сопротивления (x)

Первый метод линеаризации, который мы обсудим в этой статье, показан на рисунке 3. Давайте сначала рассмотрим основную идею этого метода, а затем посмотрим, как схема на рисунке 3 реализует эту идею.

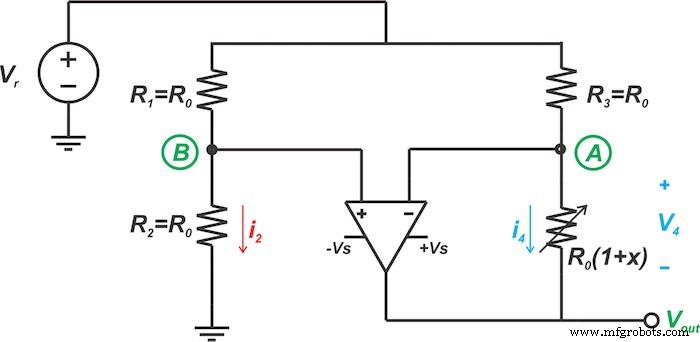
Рисунок 3. Один тип схемы для линеаризации мостов резистивных датчиков

На рисунке 4 показано изображение фиксированного тока \ [I_ {Ref} \] . вынужден протекать через наш линейный датчик.

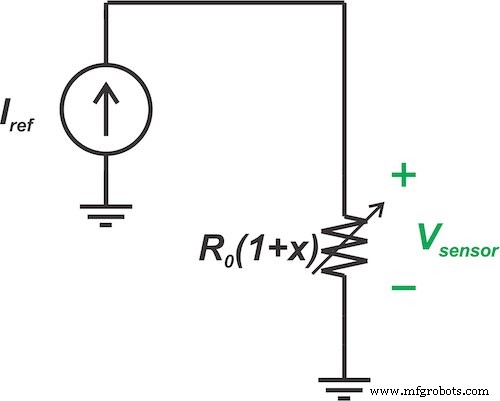
Рисунок 4. Фиксированный ток (I _Ref ) проталкивается через линейный датчик

В этом случае результирующее напряжение на датчике будет:

\ [V_ {sensor} =I_ {Ref} \ times R_0 (1 + x) \]

который можно изменить как:

\ [V_ {sensor} =R_0 \ times I_ {Ref} + R_0 \ times I_ {Ref} \ times x \]

В то время как первый член является постоянной величиной, второй член пропорционален изменениям сопротивления датчика (x). Если мы можем опустить постоянный член, у нас будет напряжение, которое имеет линейную зависимость от x.

Реализация схемы

Схема на рисунке 3 использует вышеупомянутую идею для линеаризации мостовой схемы. Поскольку в идеале входы операционного усилителя не потребляют ток, напряжение в узле B будет иметь постоянное значение:

\ [v_B =\ frac {R_0} {R_0 + R_0} V_r =\ frac {V_r} {2} \]

Отрицательная обратная связь вместе с высоким коэффициентом усиления операционного усилителя заставит как инвертирующие, так и неинвертирующие входы операционного усилителя иметь одинаковое напряжение:

\ [v_A =v_B =\ frac {V_r} {2} \]

Поскольку оба конца R3 находятся под постоянным потенциалом, через него будет течь постоянный ток. Другими словами, операционный усилитель заставляет R3 действовать как источник тока, который проталкивает в датчик постоянный ток \ [\ frac {V_r} {2R_0} \]. Следовательно, напряжение на датчике будет:

\ [V_4 =\ frac {V_r} {2R_0} \ times R_0 (1 + x) =\ frac {V_r} {2} + \ frac {V_r} {2} х \]

Первый член - это постоянное значение, которое следует исключить из V _out уравнение. Второй член пропорционален изменению сопротивления датчика (x) и должен появиться в выходном уравнении. Применяя закон напряжения Кирхгофа, находим V _out как:

\ [V_ {out} =-V_4 + V_A =- \ left (\ frac {V_r} {2} + \ frac {V_r} {2} x \ right) + V_A \]

Следовательно, нам нужен только V _A быть равным \ [\ frac {V_r} {2} \]. Это уже выполнено, что приводит к:

\ [V_ {out} =- \ frac {V_r} {2} x \]

Следовательно, выход имеет линейную зависимость от x.

Метод 2:Создание тока, пропорционального изменениям сопротивления (x)

Второй метод линеаризации моста, который мы обсудим в этой статье, показан на рисунке 5.

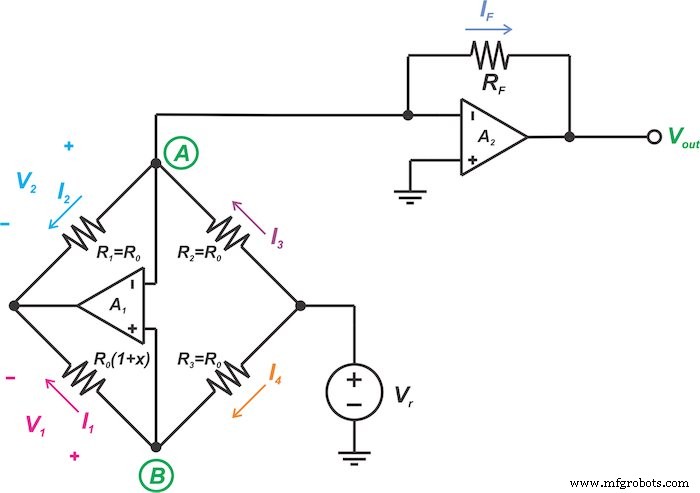
Рисунок 5. Еще одна схема аналоговой линеаризации мостов резистивных датчиков

Давайте еще раз рассмотрим основную идею этой техники, а затем рассмотрим ее схемную реализацию.

Этот второй метод линеаризации показан на рисунке 6.

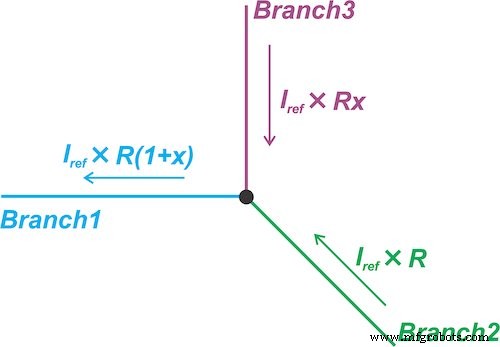
Рисунок 6. Техника линеаризации, при которой ток через ответвление цепи пропорционален сопротивлению датчика

Он заставляет ток через ветвь цепи (ветвь 1) быть пропорционален сопротивлению датчика:

\ [I_1 =I_ {Ref} \ times R_0 (1 + x) \]

где я _Ref - постоянное значение. Затем он выполняет вычитание текущего домена, чтобы удалить постоянный член \ [I_ {Ref} \ times R_0 \]. С этой целью ток через Ветвь 2 устанавливается равным \ [I_ {Ref} \ times R_0 \]. Следовательно, ток через Ветвь 3 будет \ [I_ {Ref} \ times R_0x \] - пропорционально изменению сопротивления датчика (x).

Реализация схемы

Давайте посмотрим, как схема на рисунке 5 реализует вышеупомянутую идею. Опять же, отрицательная обратная связь вместе с высоким коэффициентом усиления операционных усилителей заставит как инвертирующие, так и неинвертирующие входы двух операционных усилителей (оба A ₁ и A ₂ ) на одинаковое напряжение:

\ [v_A =v_B =0 \]

Уравнение 3

Следовательно, мы имеем V ₁ =V ₂ что приводит к

\ [R_0 (1 + x) \ times I_1 =R_0 \ times I_2 \]

Это упрощает:

\ [I_2 =I_1 + I_1 \ times x \]

Уравнение 4.

Мы знаем, что я ₁ =Я ₄ и, принимая во внимание уравнение 3, мы имеем:

\ [I_1 =I_4 =\ frac {V_r - v_A} {R_0} =\ frac {V_r} {R_0} \]

Подставляя это в уравнение 4, получаем:

\ [I_2 =\ frac {V_r} {R_0} + \ frac {V_r} {R_0} \ times x \]

Следовательно, I ₂ представляет собой сумму постоянного значения и члена, пропорционального x. Нам нужно только использовать закон Кирхгофа, чтобы исключить постоянный член в уравнении выходного тока. Ток через R2 дает ток, равный \ [\ frac {V_r} {R_0} \] к узлу A, ведущему к:

\ [I_F =- \ frac {V_r} {R_0} \ times x \]

Следовательно, получаем:

\ [V_ {out} =V_r \ times \ frac {R_F} {R_0} \ times x \]

Схема на рисунке 5 требует дополнительного операционного усилителя по сравнению с первым методом. Однако с двумя решениями на операционных усилителях мы можем произвольно установить коэффициент усиления, выбрав соотношение \ [\ frac {R_F} {R_0} \].

<час />

Чтобы увидеть полный список моих статей, посетите эту страницу.