Как использовать простой пример нейронной сети персептрона для классификации данных

В этой статье демонстрируются основные функции нейронной сети Perceptron и объясняется цель обучения.

Эта статья является частью серии, посвященной нейронным сетям Perceptron.

Если вы хотите начать с самого начала или забегать вперед, вы можете ознакомиться с другими статьями здесь:

1. Как выполнить классификацию с помощью нейронной сети:что такое перцептрон?
2. Как использовать простой пример нейронной сети персептрона для классификации данных
3. Как обучить базовую нейронную сеть персептрона
4. Общие сведения об обучении простой нейронной сети
5. Введение в теорию обучения нейронных сетей.
6. Скорость обучения в нейронных сетях
7. Расширенное машинное обучение с многоуровневым персептроном
8. Функция активации сигмовидной кишки:активация в многослойных перцептронных нейронных сетях.
9. Как обучить многослойную нейронную сеть персептрона
10. Понимание формул обучения и обратного распространения ошибки для многослойных персептронов
11. Архитектура нейронной сети для реализации Python
12. Как создать многослойную нейронную сеть персептрона на Python.
13. Обработка сигналов с использованием нейронных сетей:проверка при проектировании нейронных сетей
14. Обучающие наборы данных для нейронных сетей:как обучить и проверить нейронную сеть Python

Что такое однослойный персептрон?

В предыдущей статье мы видели, что нейронная сеть состоит из взаимосвязанных узлов, расположенных по слоям. Узлы на входном уровне распределяют данные, а узлы на других уровнях выполняют суммирование, а затем применяют функцию активации. Связи между этими узлами имеют весовой коэффициент, что означает, что каждое соединение умножает переданные данные на скалярное значение.

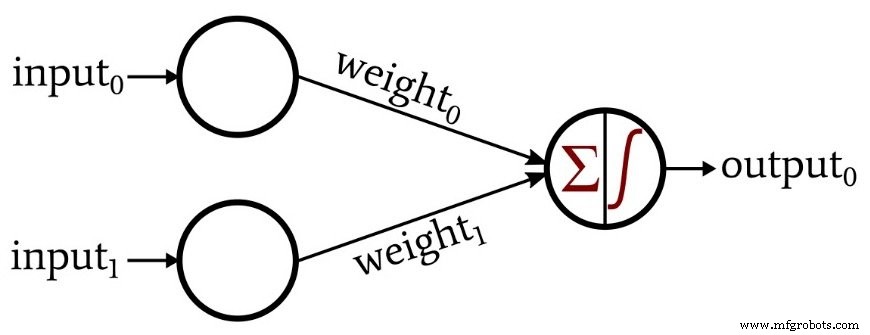
Обратите внимание, что эта конфигурация называется однослойным персептроном. Да, я знаю, у него два слоя (входной и выходной), но только один слой, содержащий вычислительные узлы.

Классификация с помощью персептрона

В этой статье мы исследуем функциональность персептрона с помощью следующей нейронной сети.

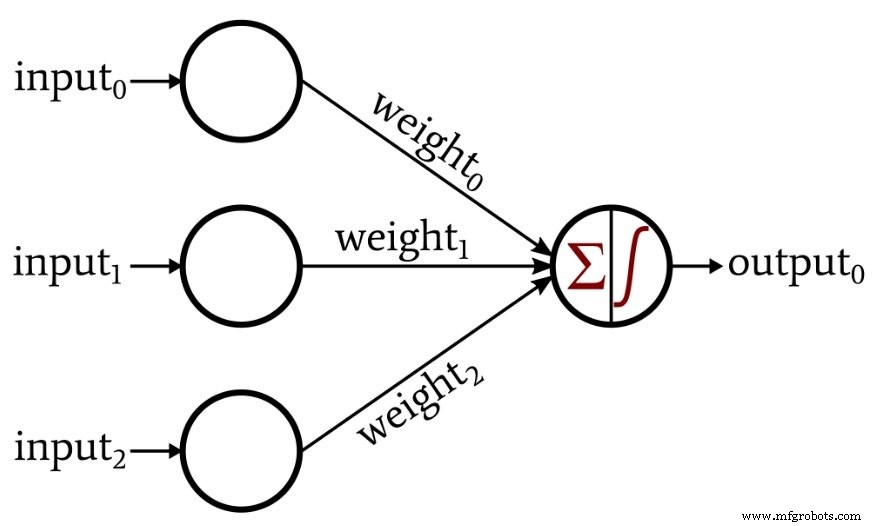
Как видите, наша входная размерность равна трем. Мы можем думать об этом персептроне как об инструменте для решения задач в трехмерном пространстве. Например, давайте предложим следующую проблему:если точка в трехмерном пространстве расположена ниже оси x, это соответствует недопустимой системе координат. Если точка находится на оси x или выше, это соответствует действительной системе отсчета, которую необходимо сохранить для дальнейшего анализа. Нам нужна эта нейтральная сеть для категоризации наших данных, при этом выходное значение 1 указывает на действительные данные, а значение 0 указывает на недопустимые данные.

Во-первых, мы должны сопоставить наши трехмерные координаты с входным вектором. В этом примере введите ₀ это компонент x, input ₁ - компонент y, и введите ₂ - z-компонента. Далее нам нужно определить веса. Этот пример настолько прост, что нам не нужно обучать сеть. Мы можем просто подумать о необходимых весах и назначить их:

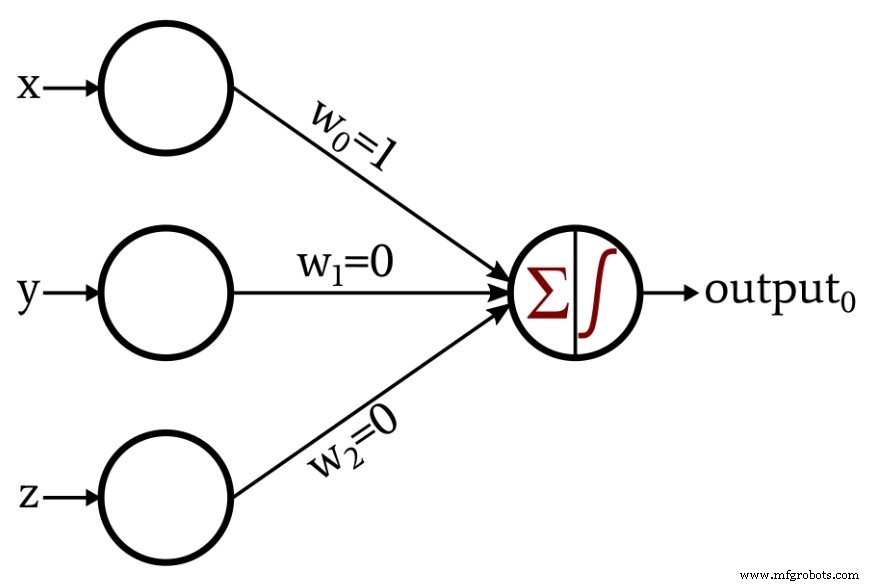
Все, что нам нужно сделать сейчас, это указать, что функция активации выходного узла представляет собой единичный шаг, выраженный следующим образом:

\ [f (x) =\ begin {cases} 0 &x <0 \\ 1 &x \ geq 0 \ end {ases} \]

Персептрон работает следующим образом:Поскольку w ₁ =0 и w ₂ =0, компоненты y и z не вносят вклад в суммирование, генерируемое выходным узлом. Единственные входные данные, которые влияют на суммирование, - это компонент x, который доставляется в выходной узел без изменений, потому что w ₀ =1. Если точка в трехмерном пространстве находится ниже оси x, суммирование выходного узла будет отрицательным, и функция активации преобразует это отрицательное значение в выходное ₀ =0. Если точка в трехмерном пространстве находится на оси x или выше, сумма будет равна или больше нуля, и функция активации преобразует это в выходной ₀ =1.

Решение проблем с персептроном

В предыдущем разделе я описал наш Perceptron как инструмент для решения проблем. Однако вы, возможно, заметили, что перцептрон не очень хорошо решал проблемы - Я решил проблему и дал решение Перцептрону, присвоив требуемые веса.

На этом этапе мы подошли к ключевой концепции нейронной сети:я смог быстро решить проблему допустимой / недопустимой классификации, потому что связь между входными данными и желаемыми выходными значениями очень проста. Однако во многих реальных ситуациях человеку будет чрезвычайно сложно сформулировать математическую связь между входными данными и выходными значениями. Мы можем получать входные данные и записывать или генерировать соответствующие выходные значения, но у нас нет математического маршрута от входа к выходу.

Полезный пример - распознавание почерка. Допустим, у нас есть изображения рукописных символов, и мы хотим разделить эти изображения на категории «a», «b», «c» и т. Д., Чтобы мы могли преобразовать рукописный текст в обычный компьютерный текст. Любой, кто умеет писать и читать, сможет сгенерировать входные изображения, а затем назначить правильные категории каждому изображению. Таким образом, сбор входных данных и соответствующих выходных данных несложен. С другой стороны, было бы чрезвычайно сложно взглянуть на пары ввода-вывода и сформулировать математическое выражение или алгоритм, который правильно преобразовал бы входные изображения в категорию вывода.

Таким образом, распознавание почерка и многие другие задачи обработки сигналов представляют собой математические проблемы, которые люди не могут решить без помощи сложных инструментов. Несмотря на то, что нейронные сети не могут думать, анализировать и внедрять новшества, они позволяют нам решать эти сложные проблемы, потому что они могут делать то, что люди не могут, то есть быстро и многократно выполнять вычисления с потенциально огромными объемами числовых данных. .

Обучение сети

Процесс, который позволяет нейронной сети создавать математический путь от входа к выходу, называется обучением. Мы даем данные для обучения сети, состоящие из входных значений и соответствующих выходных значений, и к этим значениям применяется фиксированная математическая процедура. Цель этой процедуры - постепенно изменять веса сети, чтобы сеть могла вычислять правильные выходные значения даже с входными данными, которых она никогда раньше не видела. По сути, это поиск закономерностей в обучающих данных и генерация весов, которые позволят получить полезный результат, применяя эти шаблоны к новым данным.

На следующей диаграмме показан действительный / недопустимый классификатор, рассмотренный выше, но веса другие. Это веса, которые я получил при обучении персептрона с 1000 точками данных. Как видите, процесс обучения позволил персептрону автоматически аппроксимировать математическое соотношение, которое я определил с помощью критического мышления в человеческом стиле.

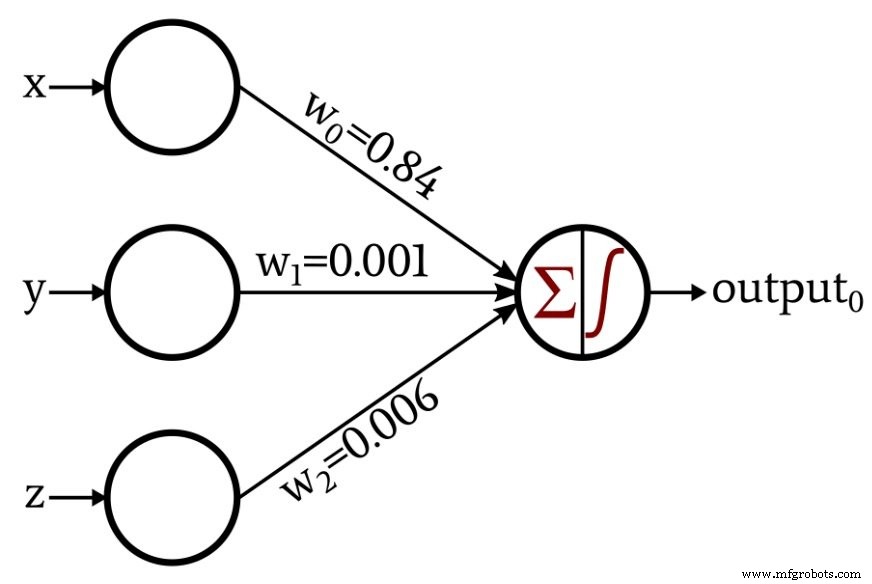
В следующей статье…

Я показал вам результаты тренировки этого персептрона, но ничего не сказал о том, как я получил эти результаты. В следующей статье будет описана короткая программа на Python, которая реализует однослойную нейронную сеть Perceptron, а также я объясню свою процедуру обучения.