Лучшие практики суммирования допусков

Наложение допусков, также известное как наложение допусков, относится к комбинации допусков различных размеров детали. После определения допуска на размер детали , важно проверить, будет ли этот допуск работать с инструментом допуски:либо верхний конец, либо нижний конец. Деталь или сборка могут иметь неточности, если их допуски установлены неправильно.

Важность допусков

Допуски напрямую влияют на стоимость и характеристики продукта. Более жесткие допуски делают обрабатываемую деталь более сложной в производстве и, следовательно, часто более дорогой. Учитывая это, важно найти баланс между технологичностью детали, ее функциональностью и стоимостью.

Советы по успешному объединению допусков

Избегайте использования излишне малых допусков

Как указано выше, более жесткие допуски приводят к более высокой стоимости производства, поскольку деталь сложнее изготовить. Эта более высокая стоимость часто связана с увеличением количества выбрасываемых деталей, которые могут возникнуть, когда обнаруживается, что размеры выходят за допустимые пределы. Стоимость высококачественных держателей инструментов и инструментов с более жесткими допусками также может быть дополнительным расходом.

Кроме того, излишне малые допуски приведут к увеличению времени изготовления, так как требуется больше работы, чтобы убедиться, что деталь соответствует строгим критериям во время обработки и после обработки в процессе контроля.

Будьте осторожны, чтобы не увеличить размер детали

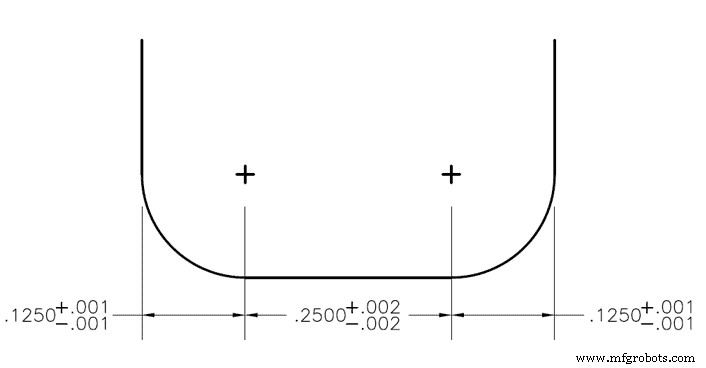
Когда верхний и нижний допуск отмечен на каждой детали детали, завышение размеров может стать проблемой. Например, концевая фреза с угловым радиусом с правым и левым угловыми радиусами может иметь допуск +/- 0,001 дюйма, а плоскость между ними имеет допуск 0,002 дюйма. В этом случае окно допуска для диаметра фрезы будет +/- 0,004 дюйма, но часто неправильно рассчитывается при определении размеров детали. Кроме того, размещение допуска на этой выноске приведет к тому, что она будет иметь избыточный размер, поэтому необходимо оставить справочный размер «REF», чтобы занять место допуска.

Использовать статистический анализ допусков:

Статистический анализ рассматривает вероятность того, что все три допуска будут ниже или выше заданной ширины паза, исходя из стандартного отклонения. Эта вероятность представлена ​​нормальной функцией плотности вероятности, которую можно увидеть на рисунке 2 ниже. Комбинируя все вероятности различных частей и размеров в конструкции, мы можем определить вероятность того, что деталь будет иметь проблемы или вообще выйдет из строя, на основе размеров и допусков деталей. Как правило, этот метод анализа используется только для сборок с четырьмя и более допусками.

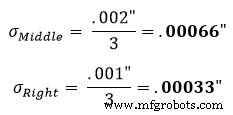
Перед началом статистического анализа допусков необходимо рассчитать или выбрать коэффициент распределения допусков. Стандартное распределение 3 . Это означает, что большинство данных (или, в данном случае, допуски) будут находиться в пределах 3 стандартных отклонений от среднего значения. Стандартные отклонения всех допусков должны быть разделены на этот коэффициент распределения допусков, чтобы нормализовать их от распределения 3 до распределения 1 . Как только это будет сделано, из квадрата суммы корней можно найти стандартное отклонение сборки.

Думайте об этом как о чашке кофе, приготовленной из трех зерен разного размера. Чтобы приготовить вкусную чашку джо, вы должны сначала смолоть все зерна до одинакового размера, чтобы их можно было добавить в кофейный фильтр. В этом случае зерна — это стандартные отклонения, кофемолка — коэффициент распределения допусков, а кофейный фильтр — уравнение квадрата корня. Это необходимо, поскольку некоторые допуски могут иметь разные коэффициенты распределения в зависимости от плотности диапазона допусков.

Метод статистического анализа используется, если требуется, чтобы паз был шириной 0,500 дюйма с допуском +/- 0,003 дюйма, но нет необходимости в радиусах (0,125 дюйма) и плоскости (0,250 дюйма). ), если быть точным, если они помещаются в слот. В этом примере у нас есть 3 двусторонних допуска с уже доступными стандартными отклонениями. Поскольку они двусторонние, стандартное отклонение от среднего будет просто равно значению допуска + или -. Для внешних радиусов это будет 0,001 дюйма, а для средней плоской области это будет 0,002 дюйма.

Для этого примера давайте найдем стандартное отклонение (σ) каждого раздела, используя уравнение 1. В этом уравнении представлено стандартное отклонение.

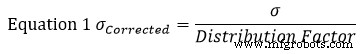
Стандартное предположение состоит в том, что допуск детали представляет нормальное распределение +/- 3. Следовательно, коэффициент распределения будет равен 3. Используя уравнение 1 в левой части рисунка 1, мы находим, что его скорректированное стандартное отклонение равняется:

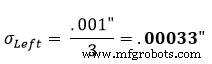
Затем это повторяется для средней и правой частей:

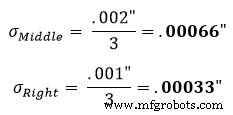
Получив эти стандартные отклонения, мы вводим результаты в уравнение 2, чтобы найти стандартное отклонение зоны допуска. Уравнение 2 известно как уравнение квадрата суммы корней.

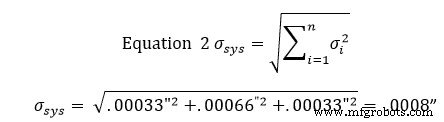
На данный момент это означает, что 68% слотов будут находиться в пределах допуска +/- 0,0008 дюйма. Умножение этого допуска на 2 приведет к доверительному окну 95 %, а умножение его на 3 приведет к доверительному окну 99 %.

68% слотов будут в пределах +/- 0,0008”

95% слотов будут в пределах +/- 0,0016”

99% слотов будут в пределах +/- 0,0024”

Эти доверительные интервалы являются стандартными для нормально распределенного набора точек данных. Стандартное нормальное распределение можно увидеть на рисунке 2 выше.

Статистический анализ допусков следует использовать только для сборок, содержащих более 4 деталей с допусками. Многие факторы не были учтены в этом простом анализе. Этот пример относится к трем двусторонним размерам, допуски которых представляют их стандартные отклонения от их средних значений. При стандартном статистическом анализе допусков в игру вступают другие переменные, такие как углы, биение и параллельность, для которых требуются поправочные коэффициенты.

Знаете ли вы, что бренды Harvey Performance Company сотрудничают с лучшими в отрасли поставщиками программного обеспечения для камер для предоставления библиотек инструментов?

Нажмите здесь, чтобы узнать больше

Использовать анализ наихудшего случая:

Анализ наихудшего случая — это практика сложения всех допусков детали для определения общего допуска детали. При выполнении этого типа анализа каждый допуск устанавливается на его наибольший или наименьший предел в соответствующем диапазоне. Затем этот общий допуск можно сравнить с пределами производительности детали, чтобы убедиться, что сборка спроектирована правильно. Обычно это используется только для одного размера (только для одной плоскости, поэтому углы не используются) и для сборок с небольшим количеством деталей.

Анализ наихудшего случая также можно использовать при выборе соответствующего режущего инструмента для вашей работы, поскольку допуск инструмента можно добавить к допуску детали для наихудшего сценария. Как только этот сценарий определен, машинист или инженер может внести соответствующие коррективы, чтобы сохранить деталь в пределах размеров, указанных на отпечатке. Следует отметить, что наихудший сценарий редко встречается в реальном производстве. Хотя эти анализы могут быть дорогостоящими для производства, они обеспечивают спокойствие машинистам, гарантируя, что все узлы будут функционировать должным образом. Часто этот метод требует строгих допусков, потому что общий стек при максимальных условиях является основной характеристикой, используемой при проектировании. Более жесткие допуски увеличивают производственные затраты из-за увеличения количества шабрения, времени производства для проверки и стоимости инструментов, используемых для этих деталей.

Пример наихудшего сценария в контексте рисунка 1:

Найдите нижний предел спецификации.

Для радиуса левого угла

0,125” – 0,001” =0,124”

Для плоской секции

0,250” – 0,002” =0,248”

Для правильного углового радиуса

0,125” – 0,001” =0,124”

Добавьте все это вместе к нижнему пределу спецификации:

0,124 дюйма + 0,248 дюйма + 0,124 дюйма =0,496 дюйма

Найдите верхний предел спецификации:

Для радиуса левого угла

0,125 дюйма + 0,001 дюйма =0,126 дюйма

Для плоской секции

0,250 дюйма + 0,002 дюйма =0,252 дюйма

Для правильного углового радиуса

0,125 дюйма + 0,001 дюйма =0,126 дюйма

Добавьте все это вместе к нижнему пределу спецификации:

0,126 дюйма + 0,252 дюйма + 0,126 дюйма =0,504 дюйма

Вычтите два и разделите этот ответ на два, чтобы получить наихудший допуск:

(Верхний предел – Нижний предел)/2 =0,004”

Таким образом, наихудший сценарий для этого слота – 0,500 +/- 0,004 дюйма

.