Методы анализа последовательно-параллельных резисторных цепей
Рекомендации по анализу последовательно-параллельных цепей
Цель анализа последовательно-параллельной цепи резисторов - определить все падения напряжения, токи и рассеиваемую мощность в цепи. Общая стратегия достижения этой цели заключается в следующем:
- Шаг 1: Оцените, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.
- Шаг 2: Нарисуйте схему заново, заменив каждую из комбинаций последовательных или параллельных резисторов, указанных на шаге 1, одним резистором эквивалентного номинала. Если для управления переменными используется таблица, создайте новый столбец таблицы для каждого эквивалента сопротивления.
- Шаг 3: Повторяйте шаги 1 и 2, пока вся схема не будет уменьшена до одного эквивалентного резистора.
- Шаг 4: Рассчитайте общий ток из общего напряжения и общего сопротивления (I =E / R).
- Шаг 5. Взяв значения общего напряжения и полного тока, вернитесь к последнему этапу процесса сокращения цепи и вставьте эти значения, где это возможно.
- Шаг 6: Из известных сопротивлений и значений полного напряжения / общего тока из шага 5 используйте закон Ома для вычисления неизвестных значений (напряжения или тока) (E =IR или I =E / R).
- Шаг 7. Повторяйте шаги 5 и 6, пока все значения напряжения и тока не будут известны в исходной конфигурации схемы. По сути, вы будете шаг за шагом переходить от упрощенной версии схемы к ее исходной сложной форме, вставляя значения напряжения и тока, где это необходимо, до тех пор, пока не будут известны все значения напряжения и тока.
- Шаг 8. Рассчитайте рассеиваемую мощность на основе известных значений напряжения, тока и / или сопротивления.
Пример анализа последовательно-параллельной комбинированной схемы
Это может показаться пугающим процессом, но его гораздо легче понять на примере, чем через описание.

Расчет параллельных сопротивлений
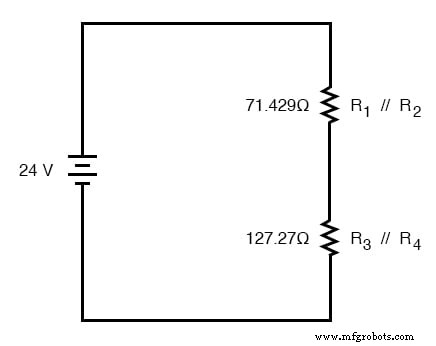
В приведенном выше примере схемы R 1 и R 2 соединены простым параллельным расположением, как и R 3 и R 4 . После идентификации эти секции необходимо преобразовать в эквивалентные одиночные резисторы и перерисовать схему:

Символы двойной косой черты (//) обозначают «параллельность», чтобы показать, что эквивалентные значения резисторов были рассчитаны с использованием формулы 1 / (1 / R). Резистор 71,429 Ом в верхней части схемы эквивалентен R 1 и R 2 параллельно друг другу. Резистор 127,27 Ом внизу эквивалентен R 3 и R 4 параллельно друг другу.
Нашу таблицу можно расширить, включив эти эквиваленты резисторов в их собственные столбцы:
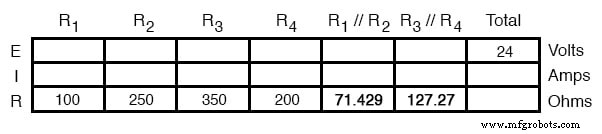
Теперь должно быть очевидно, что схема была уменьшена до простой последовательной конфигурации только с двумя (эквивалентными) сопротивлениями. Последний шаг в уменьшении - сложение этих двух сопротивлений, чтобы получить общее сопротивление цепи. Когда мы складываем эти два эквивалентных сопротивления, мы получаем сопротивление 198,70 Ом.
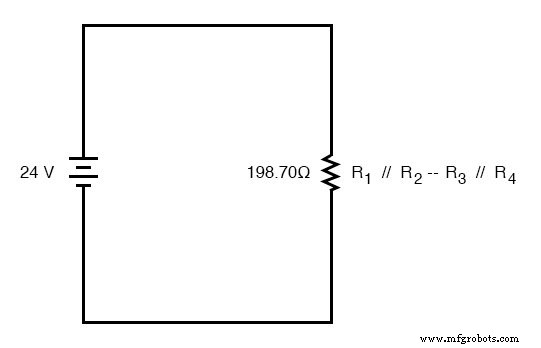
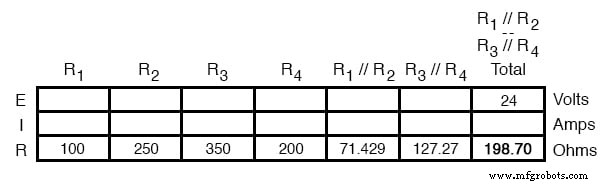
Теперь мы можем перерисовать схему как одно эквивалентное сопротивление и добавить значение общего сопротивления в крайний правый столбец нашей таблицы. Обратите внимание, что столбец «Итого» был переименован (R 1 // R 2 —R 3 // R 4 ), чтобы указать, как он электрически связан с другими столбцами рисунков. Символ «-» здесь используется для обозначения «серии», так же как символ «//» используется для обозначения «параллельности».
Расчет для тока и напряжения
Теперь общий ток цепи можно определить, применив закон Ома (I =E / R) к столбцу «Всего» в таблице:
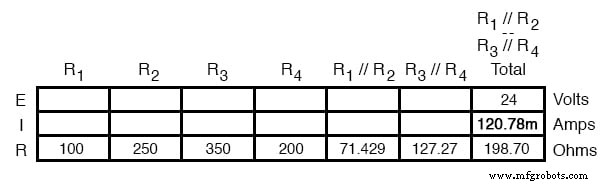
Возвращаясь к нашему чертежу эквивалентной схемы, здесь показано наше общее значение тока 120,78 миллиампер в качестве единственного тока:
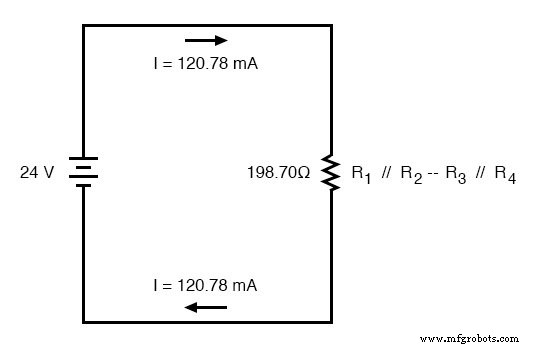
Теперь мы начинаем работать в обратном направлении в нашей прогрессии переделки схем до исходной конфигурации. Следующим шагом будет переход к схеме, где R 1 // R 2 и R 3 // R 4 идут последовательно:
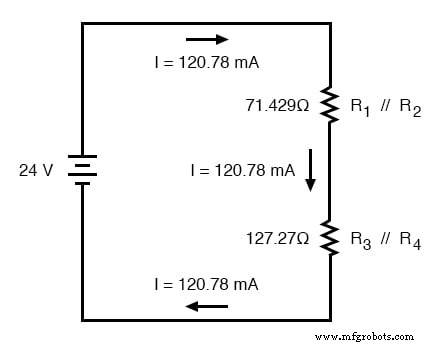
Поскольку R 1 // R 2 и R 3 // R 4 соединены последовательно друг с другом, ток через эти два набора эквивалентных сопротивлений должен быть одинаковым. Кроме того, ток через них должен быть таким же, как и общий ток, поэтому мы можем заполнить нашу таблицу соответствующими текущими значениями, просто скопировав текущую цифру из столбца Total в R 1 // R 2 и R 3 // R 4 столбцы:
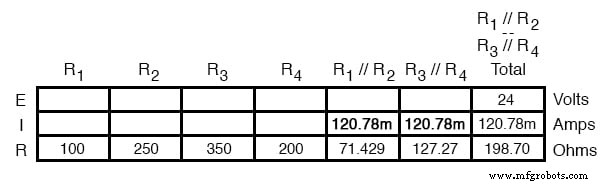
Теперь, зная ток через эквивалентные резисторы R 1 // R 2 и R 3 // R 4 , мы можем применить закон Ома (E =IR) к двум правым вертикальным столбцам, чтобы найти падение напряжения на них:
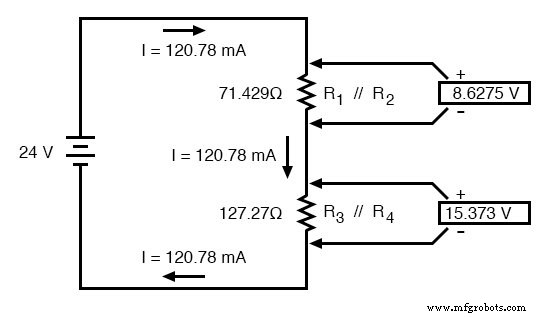
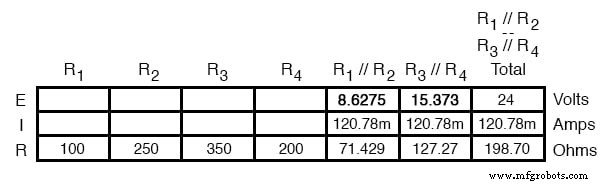
Потому что мы знаем R 1 // R 2 и R 3 // R 4 являются эквивалентами параллельных резисторов, и мы знаем, что падения напряжения в параллельных цепях одинаковы, мы можем перенести соответствующие падения напряжения в соответствующие столбцы таблицы для этих отдельных резисторов. Другими словами, мы делаем еще один шаг назад в нашей последовательности рисования к исходной конфигурации и заполняем таблицу соответствующим образом:
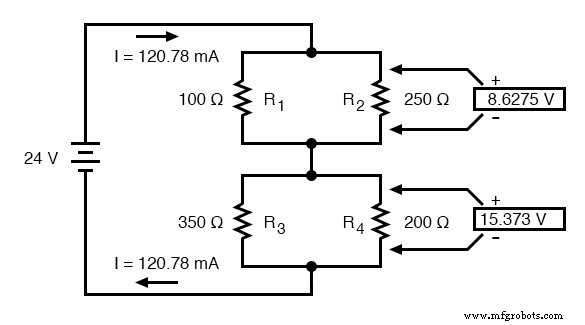
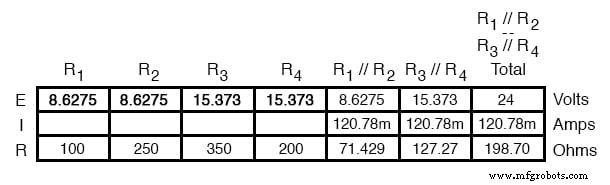
Наконец, исходный раздел таблицы (столбцы R 1 через R 4 ) содержит достаточно значений для завершения. Применяя закон Ома к остальным вертикальным столбцам (I =E / R), мы можем определить токи через R 1 , R 2 , R 3 , и R 4 индивидуально:
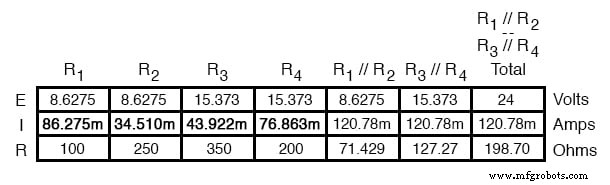
Размещение значений напряжения и тока на диаграммах
Найдя все значения напряжения и тока для этой схемы, мы можем показать эти значения на принципиальной схеме как таковые:
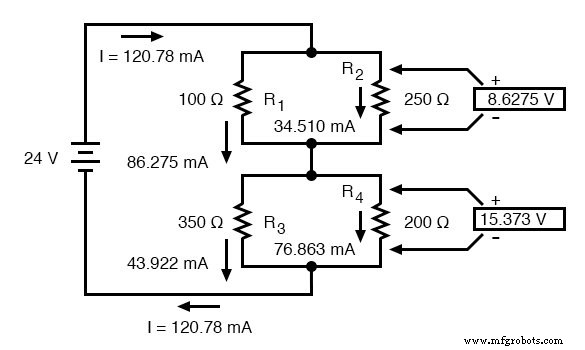
В качестве последней проверки нашей работы мы можем увидеть, складываются ли рассчитанные текущие значения должным образом в общую сумму. Поскольку R 1 и R 2 соединены параллельно, их комбинированные токи в сумме должны составить 120,78 мА. Аналогично, поскольку R 3 и R 4 включены параллельно, их комбинированные токи в сумме также должны составить 120,78 мА. Вы можете сами убедиться, что эти цифры совпадают, как и ожидалось.
Использование SPICE для проверки вычисленных значений
Компьютерное моделирование также может использоваться для проверки точности этих цифр. Следующий анализ SPICE покажет все напряжения и токи резисторов (обратите внимание на чувствительные к току vi1, vi2, ... «фиктивные» источники напряжения, включенные последовательно с каждым резистором в списке соединений, необходимые для компьютерной программы SPICE для отслеживания тока на каждом пути. ). Каждый из этих источников напряжения будет настроен на нулевое напряжение, поэтому они никоим образом не повлияют на схему.
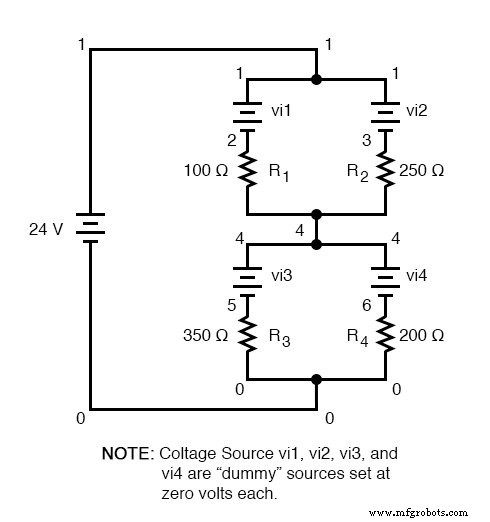
последовательно-параллельная цепь v1 1 0 vi1 1 2 постоянного тока 0 vi2 1 3 постоянного тока 0 г1 2 4 100 г2 3 4 250 vi3 4 5 постоянного тока 0 vi4 4 6 постоянного тока 0 г3 5 0 350 г4 6 0200 .dc v1 24 24 1 .print dc v (2,4) v (3,4) v (5,0) v (6,0) .print dc i (vi1) i (vi2) i (vi3) i (vi4) .конец
Я снабдил выходные данные SPICE аннотациями, чтобы сделать их более читаемыми, обозначив, какие значения напряжения и тока относятся к каким резисторам.
Как видите, все цифры согласуются с расчетными значениями.
ОБЗОР:
- Чтобы проанализировать последовательно-параллельную комбинированную схему, выполните следующие действия:
- Сократите исходную схему до одного эквивалентного резистора, перерисовывая схему на каждом этапе уменьшения, поскольку простые последовательные и простые параллельные части сокращаются до отдельных эквивалентных резисторов.
- Найдите полное сопротивление.
- Найдите общий ток (I =E / R).
- Определите эквивалентные падения напряжения на резисторе и токи ответвления по очереди, снова работая в обратном направлении к исходной конфигурации схемы.
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:
- Таблица манипуляций с алгебраическими уравнениями для электрических цепей
- Таблица последовательно-параллельных цепей постоянного тока
Промышленные технологии



