Введение в комплексные числа

Если бы мне нужно было описать расстояние между двумя городами, я мог бы дать ответ, состоящий из одного числа в милях, километрах или какой-либо другой единице линейного измерения.

Однако, если бы я описал, как путешествовать из одного города в другой, мне пришлось бы предоставить больше информации, чем просто расстояние между этими двумя городами; Я также должен предоставить информацию о направлении и путешествовать.

Информация, которая выражает одно измерение, например линейное расстояние, называется скаляром . количество в математике. Скалярные числа - это числа, которые вы до сих пор использовали во всех своих математических приложениях.

Например, напряжение, создаваемое батареей, является скалярной величиной. Так же как и сопротивление отрезка провода (Ом) или ток через него (амперы).

Однако, когда мы начинаем анализировать цепи переменного тока, мы обнаруживаем, что величина напряжения, тока и даже сопротивления (называемая импедансом при переменном токе) не являются привычными одномерными величинами, которые мы привыкли измерять в цепях постоянного тока.

Скорее, эти величины, поскольку они динамичны (чередуются по направлению и амплитуде), обладают другими измерениями, которые необходимо учитывать. Частота и фазовый сдвиг - вот два из этих параметров, которые имеют значение.

Даже в относительно простых цепях переменного тока, где мы имеем дело только с одной частотой, нам все равно нужно бороться с измерением фазового сдвига в дополнение к амплитуде.

Для успешного анализа цепей переменного тока нам необходимо работать с математическими объектами и методами, способными представлять эти многомерные величины.

Вот где нам нужно отказаться от скалярных чисел в пользу чего-то более подходящего: комплексные числа . Как и в примере с указанием направлений из одного города в другой, величины переменного тока в одночастотной цепи имеют как амплитуду (аналогия:расстояние), так и фазовый сдвиг (аналогия:направление).

Комплексное число - это единственная математическая величина, способная одновременно выразить эти два измерения амплитуды и фазового сдвига.

Графическое представление комплексных чисел

Комплексные числа легче понять, если они представлены графически. Если я нарисую линию с определенной длиной (величиной) и углом (направлением), у меня будет графическое представление комплексного числа, которое обычно известно в физике как вектор :(Рисунок ниже)

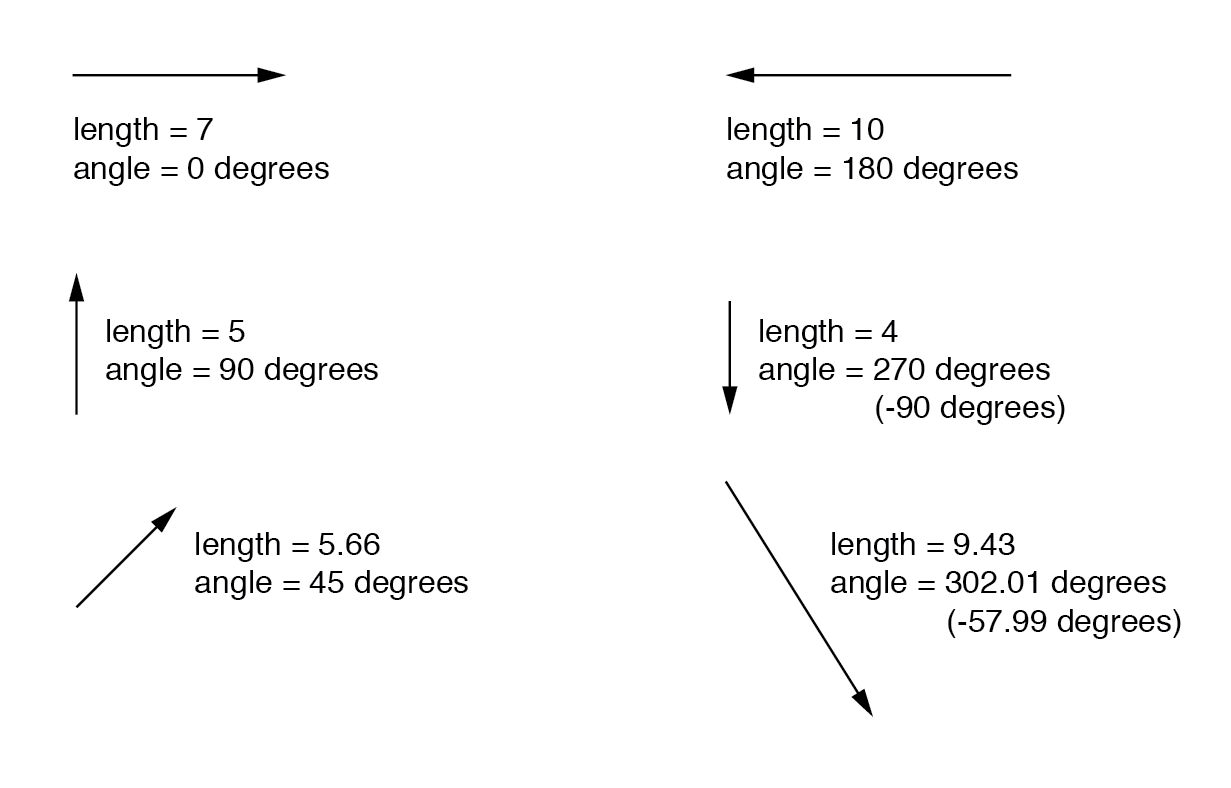
В качестве расстояний и направлений на карте должна быть какая-то общая система отсчета, чтобы значения углов имели какое-либо значение. В этом случае прямое право считается равным 0 ^o , а углы отсчитываются в положительном направлении против часовой стрелки:(рисунок ниже)

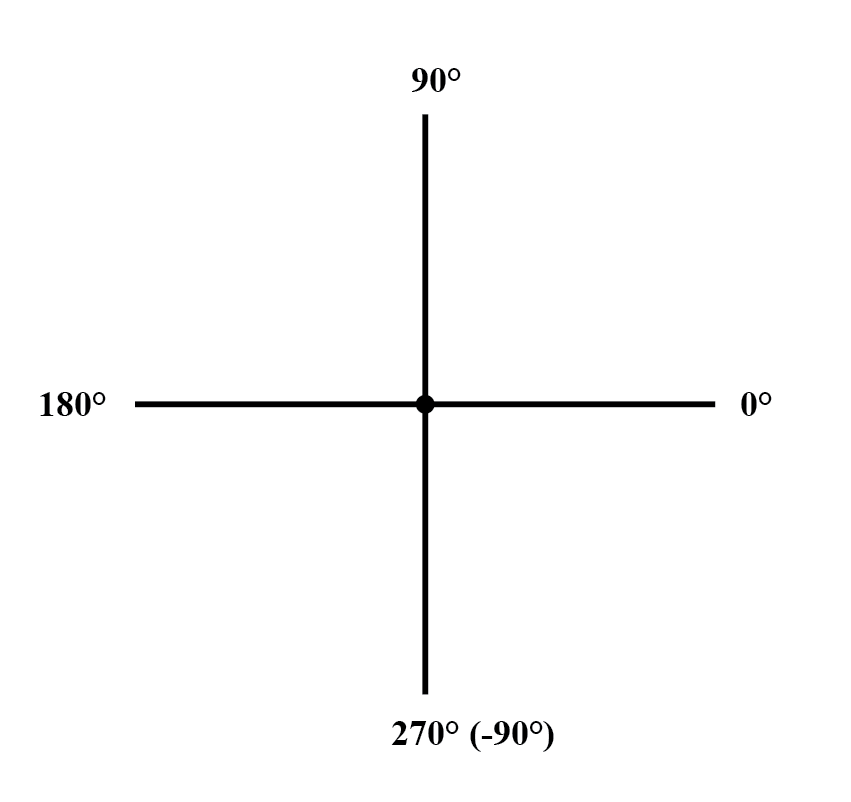
В идее представления числа в графической форме нет ничего нового. Мы все узнали об этом в начальной школе с помощью «числовой линии:» (рисунок ниже)

Мы даже узнали, как работает сложение и вычитание, увидев, как длины (величины) складываются, чтобы дать окончательный ответ:(рисунок ниже)

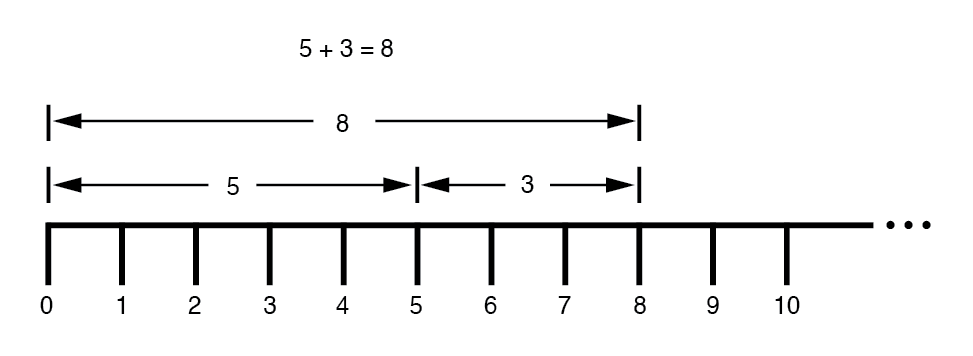
Позже мы узнали, что существуют способы обозначать значения между целые числа, отмеченные на линии. Это были дробные или десятичные величины:(рисунок ниже)

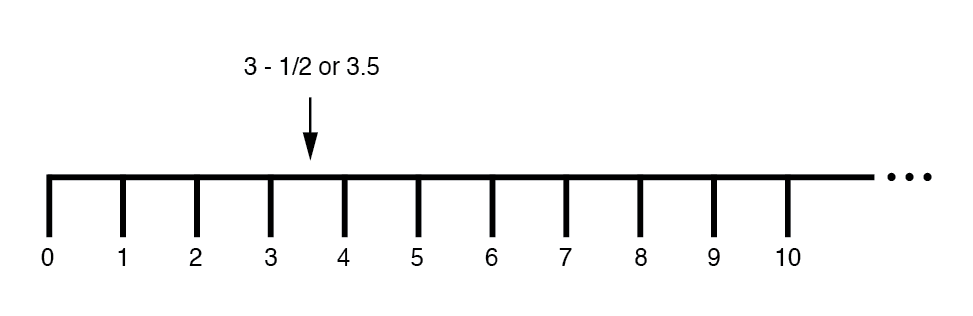
Эти поля чисел (целые, целые, рациональные, иррациональные, действительные и т. Д.), Изученные в начальной школе, имеют общую черту:все они одномерные . Это наглядно иллюстрирует прямолинейность числовой прямой.

Вы можете перемещаться вверх или вниз по числовой прямой, но все «движение» вдоль этой линии ограничено одной осью (горизонтальной).

Одномерные скалярные числа идеально подходят для подсчета бусинок, представления веса или измерения напряжения батареи постоянного тока, но они не способны представить что-то более сложное, например расстояние и направление между двумя городами или амплитуда и фаза сигнала переменного тока.

Чтобы представить такие величины, нам нужны многомерные представления. Другими словами, нам нужна числовая линия, которая может указывать в разных направлениях, и именно это и есть вектор.

ОБЗОР:

• скаляр число - это тип математического объекта, который люди привыкли использовать в повседневной жизни:одномерная величина, такая как температура, длина, вес и т. д.
• комплексное число - математическая величина, представляющая два измерения величины и направления.
• вектор является графическим изображением комплексного числа. Это похоже на стрелку с начальной точкой, концом, определенной длиной и определенным направлением. Иногда слово фазор используется в электрических приложениях, где угол вектора представляет собой фазовый сдвиг между сигналами.

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

• Рабочий лист фазы переменного тока