Производные степенных функций от e

Пример производных от e

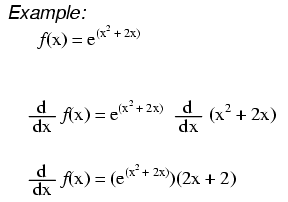
Константа пропорциональности

Когда мы говорим, что отношения или явления являются «экспоненциальными», мы подразумеваем, что некоторая величина - электрический ток, прибыль, население - увеличивается быстрее по мере роста количества. Другими словами, скорость изменения данной переменной пропорциональна значению этой переменной. Это означает, что производная экспоненциальной функции равна исходной экспоненциальной функции, умноженной на константу ( k ), устанавливающий соразмерность.

$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =ka ^ x $$

Константа пропорциональности равна натуральному логарифму основания показателя степени:

$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =\ ln (a) \ times a ^ x $$

Отсюда следует, что если натуральный логарифм основания равен единице, производная функции будет равна исходной функции. Именно это происходит со степенными функциями от e:натуральный логарифм e равен 1, и, следовательно, производная $$ e ^ x $$ равна $$ e ^ x $$.

$$ \ frac {\ text {d}} {\ text {d} x} e ^ x =e ^ x $$

Правило "цепочки"

Когда экспоненциальное выражение представляет собой нечто иное, чем просто x, мы применяем цепное правило:сначала мы берем производную всего выражения, затем мы умножаем ее на производную выражения в экспоненте.

$$ \ frac {\ text {d}} {\ text {d} x} e ^ {x ^ 2 + 2x} =e ^ {x ^ 2 + 2x} \ times \ frac {\ text {d}} { \ text {d} x} (x ^ 2 + 2x) =(2x + 2) e ^ {x ^ 2 + 2x} $$

Этот метод можно использовать для определения скорости изменения тока диода по отношению к напряжению диода. Следующее уравнение обеспечивает приблизительное соотношение между напряжением на диоде ($$ V_D $$) и током через диод ($$ I_D $$):

$$ I_D =I_S \ times e ^ \ frac {V_D} {0,026} $$

(См. Страницу о диодах и выпрямителях для получения дополнительной информации о уравнении тока диода к напряжению; также обратите внимание, что $$ I_S $$ является константой, а не переменной.) Чтобы найти скорость изменения тока по отношению к напряжению, берем производную:

$$ \ frac {\ text {d} I_D} {\ text {d} V_D} =\ frac {\ text {d}} {\ text {d} V_D} (I_S \ times e ^ \ frac {V_D} { 0,026}) =I_S \ times e ^ \ frac {V_D} {0,026} \ times \ frac {1} {0,026} $$

Таким образом, при заданном значении напряжения диода $$ V_D $$ постепенное увеличение напряжения приведет к увеличению тока, равному $$ \ frac {I_S} {0,026} e ^ \ frac {V_D} {0,026} $$ .

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист расчетов для электрических цепей